Exercice 1
Une entreprise doit réduire la quantité de déchets qu’elle rejette pour respecter une nouvelle
norme environnementale. Elle s’engage, à terme, à rejeter moins de 30 000 tonnes de déchets
par an.
En 2010, l’entreprise rejetait 40 000 tonnes de déchets.
Depuis cette date, l’entreprise réduit chaque année la quantité de déchets qu’elle rejette
de 5 % par rapport à la quantité rejetée l’année précédente, mais elle produit par ailleurs
200 tonnes de nouveaux déchets par an en raison du développement de nouvelles activités.
Pour tout entier naturel n, on note un la quantité, en tonnes, de déchets pour l’année
(2010+n). On a donc u
0 = 40000.
1. Calculer u
1 et u
2.
u
1 =0,95 u
0+200=0,95 x 40000 +200=38200.
u2 =0,95 u1+200=0,95 x 38200 +200=36490.
2. Justifier que pour tout entier naturel n, on a u
n+1 = 0,95u
n +200.
Chaque année la quantité de déchets diminue de 5 % ; l'entreprise en rejette donc 0,95 fois la quantité de l'année précédente.
A cel il faut ajouter 200 tonnes de déchets dus aux nouvelles activités.
3. On considère la suite (s
n) définie, pour tout naturel n, par s
n = u
n −4000.
Démontrer que la suite (sn) est une suite géométrique. Précisez sa raison et son premier terme.
s
n+1 = u
n+1 -4000 =0,95 u
n+200 -4000 =0,95 u
n-3800.
sn+1 = 0,95(u
n -3800 /0,95) = 0,95(u
n- 4000)=0,95 s
n.
La suite s
n est géométrique de raison q = 0,95 et de premier terme 40 000-4000 = 36 000.
4. Pour tout entier naturel n, exprimez s
n en fonction de n.
En déduire que, pour tout entier naturel n, on a u
n = 36000×0,95
n +4000.
s
n = s
0 x0,95
n =36 000 x0,95
n.
u
n = s
n +4000 =
36000×0,95n +4000.
5. Déterminer la limite de un en +∞ et commenter.
0 < 0,95 < 1, donc 0,95
n tend vers zéro si n tend vers plus l'infini.
u
n tend vers 4000, l'objectif sera respecté.
6. À partir de quelle année, le contexte restant le même, l’entreprise réussira-t-elle à respecter son engagement ?
36000×0,95n +4000 < 30 000.
36000×0,95n < 26 000 ; 0,95n < 26 / 36~0,722.
n ln(0,95) < ln(0,722) ;
n > 6,35 ; n = 7 année 2017.
Exercice 2.
Une entreprise vend des calculatrices de marque Calculmax.
Le service après-vente s’est aperçu qu’elles pouvaient présenter deux types de défauts, l’un
lié au clavier et l’autre à l’affichage.
Des études statistiques ont permis à l’entreprise d’utiliser la modélisation suivante :
La probabilité pour une calculatrice tirée au hasard de présenter un défaut de clavier est
égale à 0,04.
En présence du défaut de clavier, la probabilité que la calculatrice soit en panne d’affichage
est de 0,03.
En l’absence de défaut de clavier, la probabilité de ne pas présenter de défaut d’affichage est
de 0,94.
On notera A l’évènement « la calculatrice présente un défaut d’affichage » et
C l’évènement « la calculatrice présente un défaut de clavier ».
1. Établir l’arbre pondéré décrivant cette situation.
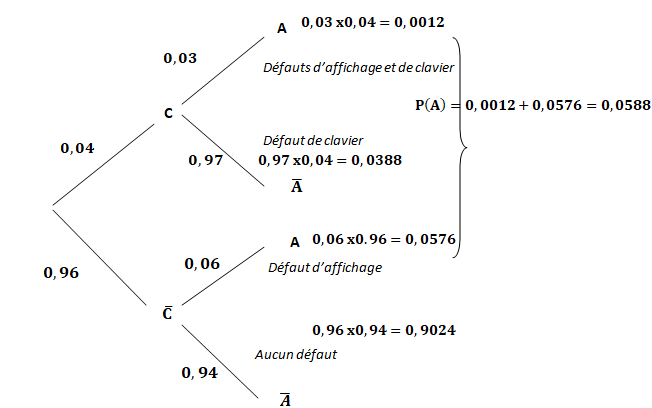 2.
2. Préciser les probabilités suivantes :
P
C ( non
A)
, P
C (A) et P(C).
La probabilité pour une calculatrice de présenter un défaut de clavier est
égale à 0,04.
p(C) =0,04 ;
En présence du défaut de clavier, la probabilité que la calculatrice soit en panne d’affichage
est de 0,03. PC (A)=0,03.
En présence du défaut de clavier, la probabilité que la calculatrice ne soit pas en panne d’affichage
est de 0,97.
PC ( non
A) =0,97.
3. On choisit au hasard une calculatrice de la marque Calculmax.
Pour cette question 3., les résultats seront donnés sous forme décimale au dix millième
près.
a. Calculer la probabilité pour que la calculatrice présente les deux défauts.
0,03 x0,04 = 0,0012.
b. Calculer la probabilité pour que la calculatrice présente le défaut d’affichage mais
pas le défaut de clavier.
0,96 x0,06 =0,0576.
c. Montrer que la probabilité que la calculatrice présente le défaut d’affichage est
0,0588.
P(A) = 0,0012 +0,0576 = 0,0588.
4. On choisit une calculatrice de la marque Calculmax qui présente le défaut d’affichage.
Calculer la probabilité qu’elle présente aussi le défaut de clavier.
Pour cette question 4. le résultat sera donné sous forme de fraction.
0,03 x 0,04 / 0,0588 =12 / 588 =4 / 196 = 1/ 49.