Physique.
Concours Ecole de Santé des Armées 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1. ( 10 points)
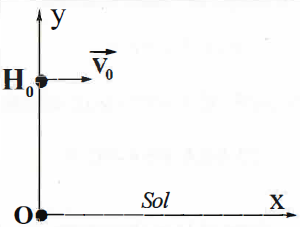
Lorsqu'une personne éternue, elle envoie vers l'avant des
milliers de petites gouttelettes où se trouvent les substances à
éliminer des voies respiratoires. On souhaite étudier le mouvement
d'une gouttelette dans le référentiel terrestre galiléen quand elle
sort de la bouche à une altitude H0 et une vitesse initiale
horizontale V0; on suppose que le poids est la seule force
exercée sur la gouttelette.
1) En utilisant la
loi de conservation de l'énergie mécanique, établir l'expression de la
vitesse Vsol de la gouttelette quand elle touche le sol en
fonction de H0, V0 et g accélération d.e la
pesanteur.
Energie mécanique initiale : ½mV02 + mgH0.
Energie mécanique finale : ½mVsol2
.
Conservation de l'énergie mécanique : ½mV02
+ mgH0 = ½mVsol2
.
V02
+ 2gH0 = Vsol2
.
Vsol =(V02 + 2gH0 )½.
2) On prend comme condition initiale
l'instant pour lequel la gouttelette sort de la bouche.
a) Établir les
équations horaires du vecteur vitesse.
Vecteur accélération : (0 ; -g).
Vecteur vitesse, primitive du vecteur accélération) : Vsol ; -gt.
b) Établir les
équations horaires du vecteur position.
Primitive du vecteur vitesse : x =Vsol t
; y =-½gt2 +H0.
c) Établir
l'équation mathématique de trajectoire y= f(x).
t = x / Vsol ; repport dans y : y = -½g x2
/ Vsol2 +H0.
d) On appelle xmax
l'abscisse atteinte au niveau du sol.
Calculer la distance xmax si H0 = 0,8 m et V0
= 10 m.s-1.
y =0= -½g xmax2 / Vsol2
+H0.
xmax2 = 2 H0Vsol2
/ g = 1,6 x100 / 10 =16 ; xmax = 4 m.
3) Avant l'éternuement, chaque
poumon est rempli d'air au maximum de sa capacité de remplissage
estimée à 1,6 L avec une pression de 105 Pa ; la température
de l'air dans les poumons est de 37°C.
Calculer la valeur du nombre de mole d'air dans chaque poumon avant
l'éternuement.
n = PV / (RT) =105 x 1,6 10-3 / (8 x(273+37))~0,065 mol.
4) Un éternuement
peut provoquer un bruit pouvant atteindre un niveau d'intensité sonore
de 80 dB.
Sachant que le niveau d'intensité sonore d'une personne lors d'une
conversation normale est de 60 dB, déterminer le nombre de personnes
devant parler en même temps pour provoquer un son de même niveau
d'intensité sonore que celui d'un très fort éternuement.
Intensité acoustique d'une personne parlant normalement : 10-12
x 106 = 10-6 W m-2.
Intensité acoustique d'une personne éternuant : 10-12
x 108 = 10-4 W m-2.
Nomnbre de personnes parlant normalement : n = 10-4 / 10-6
= 100.
Exercice 2 - (5 points)
Avant d'en réaliser sa greffe, un rein à une température initiale T0
= 5°C est plongé dans une solution à une température constante Text
= 35°C ; le rein a une masse m = 150 g, une surface S
= 300 cm2 et une capacité thermique massique Cm =
4 J .K-1.g-1. On suppose que les échanges entre
le rein et la solution obéissent à la loi de Newton dQ = h.S.(Text
- T).dt où dQ est la chaleur élémentaire échangée pendant la durée
élémentaire dt et où h est le coefficient conducto-convectif avec h = 5
unités du SI.
1) Proposer une·
unité internationale possible pour h, coefficient conducto-convectif.
h = dQ / (S.(Text - T)).
dQ s'exprime en watt ( joule / seconde) ; S en m2
et la température en kelvin.
h s'exprime en W m-2 K-1.
2) Calculer la variation d'énergie
interne du rein lorsque sa température passe de 5°C à 35°C ;
on considérera que le rein est assimilé à un système thermodynamique
incompressible.
DU = Cm
m DT = 4 x150
x(35-5) = 600 x30 =1,8 104 J.
3) En appliquant le
premier principe de la thermodynamique, montrer que lorsque le rein est
plongé dans la solution, sa température T obéit à l'équation
différentielle ci-dessous :
dT / dt +kT = k Text avec k = hS / (m cm).
DU = dQ + W avec W = 0 (
système incompressible)
Cm m dT =
h.S.(Text - T).dt.
dT / dt = hS / (Cm m)(Text - T) = k(Text - T).
dT / dt +kT=k Text .
4) Un candidat propose comme
solution de l'équation différentielle précédente :
T = [Text -T0 ].exp(-kt) + T0.
Sans utiliser l'équation différentielle, montrer que la solution
proposée est incorrecte.
Au bout d'un temps suffisamment long, exp(-kt) est nul et T tend
vers T0 =5.
Il faudrait écrire : T =
[Text -T0 ].exp(-kt) + Text.
|
...
|
....
|
Exercice 3 QCM.( 5 points).
QCM 1 (1,5 points) :
Dans le modèle atomique de Bohr de l'hydrogène, l'électron de masse m
gravite autour du noyau en décrivant une orbite circulaire uniforme de
rayon r comme décrit ci-dessous dans le repère de Frenet.
L'électron n'est soumis qu'à la force électrique dont l'expression
vectorielle est la suivante où K est une constante et où e est la
charge élémentaire.
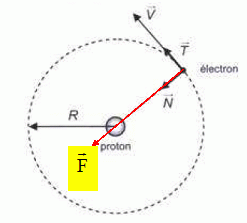
Quelle est l'expression de la norme de la vitesse V de l'électron sur
son orbite ?
L'électron n'est soumis qu'à la force
électrostatique attractive du
proton de valeur Ke2 / r2.
L'accélération et la force sont
centripètes.
Ecrire la seconde loi de Newton suivant N : Ke / r2
= mv2 / r.
mr v2 =Ke2 ; v2
= Ke2 / (mr) ; v = e[K /
(mr)]½. Réponse C.
QCM 2 (1 point) :
Un ballon rempli d'hélium, assimilé à un gaz parfait, est animé d'un
mouvement ascendant.
A. L'énergie
interne du gaz tient compte de l'énergie potentielle de pesanteur du
ballon. Faux.
B. L'énergie
interne du gaz tient compte de l'énergie cinétique du ballon lors du
mouvement. Faux.
C. L'énergie
interne d'un gaz parfait tient compte de l'énergie d'interaction entre
les molécules. Vrai.
D. La température
est la résultante des forces des chocs des molécules sur les parois du
ballon. Faux.
QCM 3 (1,5 points)
:
Un bateau B se trouve derrière une digue d'ouverture 10 m comme décrit
ci-dessous ; la digue stoppe en partie les vagues lui arrivant dessus
et présentant une longueur d'onde de 2 m. On prendra : p = 3.
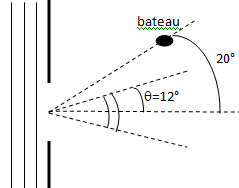
q=Longueur
d'onde / ouverture = 2 / 10 = 0,2 radian soit environ 0,2 / 3 x180 =12°.
A. La célérité des vagues est modifiée à la traversée de l'ouverture.
Faux.
B. La fréquence des vagues est modifiée à la traversée de l'ouverture.
Faux.
C. A la position où il se trouve, le bateau ne ressent pas la houle
incidente. Vrai.
D. A la position où il se trouve, le bateau ressent la houle incidente.
QCM 4 (1 point) :
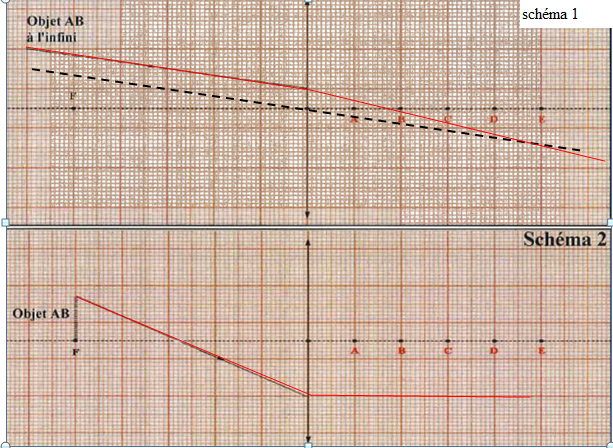
Les schémas optiques ci-dessous ne concernent que les items C et D.
A. Le grossissement d'une lunette est le rapport de la hauteur de
l'image sur celle de l'objet.
Rapport entre la
dimension de l'image sur la rétine vue à travers l'instrument et
celle obtenue à l'oeil nu.
B. Pour une lunette afocale, le foyer objet de l'objectif est confondu
au foyer image de l'oculaire.
Pour une lunette afocale,
le foyer image de l'objectif
est confondu au foyer objet de
l'oculaire.
C. Dans le schéma 1, le rayon transmis en sortie de lentille coupe
l'axe au niveau du point B. Vrai.
D. Dans le schéma 2, le rayon transmis en sortie de lentille ne coupe
pas l'axe optique. Vrai.
|
|



