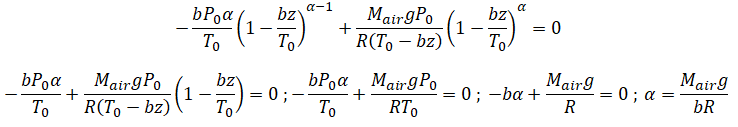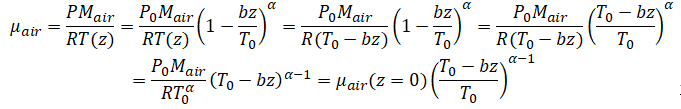Sondage des propriétés physico-chimiques de l'atmosphère par ballon stratosphérique, concours général 2023.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
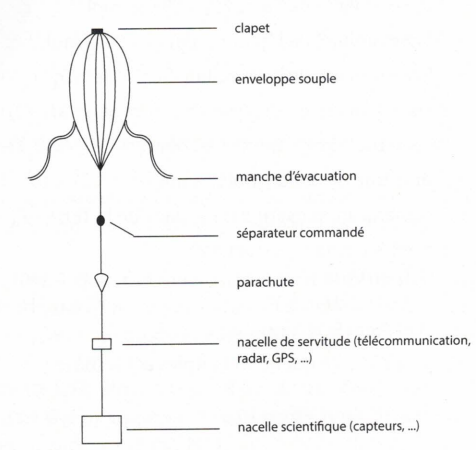
Caractéristiques du vol du ballon-sonde.

Questions préliminaires.
1.  On considère n moles d'un gaz parfait, de masse molaire M, de masse volumique µ qui occupent un volume V à la pression P et à la température T. Etablir la relation : PM =µRT.
Loi des gaz parfaits : PV = nRT.
µ = masse / V ; masse = n M ; µ =n M / V ; V = nM / µ.
P n M / µ = nRT ; PM  / µ = RT ; PM =µRT.
L'enveloppe du ballon étant ouverte sur l'extérieur via les manches d'évacuation, la pression à l'intérieur du ballon est identique à tout moment à celle qui règne à l'extérieur.
2.  . L'équilibre thermique est assuré à chaque instant entre l'hélium intérieur et l'air extérieur. Etablir la relation suivante :
µHe / µair = MHe / Mair.
Pression et température intérieures de l'hélium sont égales à la pression et température de l'air extérieur.
µ / M =P / (RT) = constante.
µHe / MHe = µair / Mair  ; µHe / µair = MHe / Mair.
 3.  Masse volumique de l'air au niveau du sol : 1,23 kg m-3 ; Mair = 29,0 g / mol ; MHe = 4,00 g / mol.
Volume initial du ballon V0 = 1,08 104 m3.
Quelle est la masse d'hélium initialement présente dans le ballon ?
MHe / Mair = 4,00 / 29,0=0,138.
 µHe / µair =0,138 ; µHe = 0,138 x 1,23 =0,170 kg m-3.
Masse d'hélium mHe = V0 µHe =1,08 104 x 0,170 =1,83 103 kg.

 Conditions de décollage.
  4. Donner l'expression du poids total du ballon rempli d'hélium en fonction de mHe, mballon et g.
mballon = 1,20 103 kg.
P = (mHe +mballon) g.
 Expression de la poussée d'Archimède à l'altitude z : F(z) = µair(z) V(z) g dirigée vers le haut.
5.Expliquer qualitativement l'origine de cette poussée.
La poussée d'Archimède est la résultante des forces de pression exercées par le fluide dans lequel se trouve le ballon.
  6. Etablir la condition  pour que le ballon puisse s'élever dans les airs depuis sa base de lancement. En déduire son volume minimal en fonction de mballon, µair(z=0), Mair et MHe.
La poussée d'Archimède doit être supérieure au poids.
µair(z=0) V(z=0) g > (mHe +mballon) g.
µair(z=0) V(z=0)  > (mHe +mballon) .
V(z=0)  > (mHe +mballon) / µair(z=0).
Or µHe / µair = MHe / Mair.
mHe =V(z=0) µHe =V(z=0)MHe µair(z=0)/ Mair.
V(z=0)  > V(z=0)MHe / Mair + mballon / µair(z=0).
V(z=0) [ 1-MHe / Mair ] > mballon / µair(z=0).
V(z=0) > mballon / [µair(z=0) [ 1-MHe / Mair ] ].
7. Calculer ce volume minimum.
V(z=0) > 1,20 103 / [1,23 (1-0,138) ]=1,13 103 m3.
Cette valeur est inférieure à V0, le ballon peut décoller.

Pour comprendre la dynamique de la phase de montée du ballon, il est nécessaire de caractériser les propriétés physiques des couches atmosphériques rencontrées.

Modélisation de la troposphère.
On s'intéresse à la couche d'atmosphère située entre 0 et 12 km ; g est constante égale à 9,8 m s-2.
8. L'air est assimilé à un gaz parfait, de pression P(z) de masse volumique µair(z) et obéit à l'équation locale de la statique des fluides : dP/dz = -µair(z) g.
Modèle de la température : T(z) = T0 -bz avec T0 = 288 K et b = 0,0059 K km-1.
Etablir l'équation suivante : dP/dz + Mair g / [R(T0-bz)] P=0.
P V = n RT ; n = m / Mair ; V / n = V Mair / m  = Mair / µair(z).
P Mair / µair(z)  =RT ; P = RT µair(z) / Mair .
µair(z)= P Mair / (RT )
dP / dz +µair(z) g = dP/dz +g Mair / (RT ) P =0.
dP/dz + Mair g / [R(T0-bz)] P=0.
9. Déterminer en fonction de Mair, g, R et b l'expression de a telle que :
P(z) = P0[1-bz / T0]a
 soit solution de l'équation précédente.
dP/dz  = -bP0 a / T0[1-bz / T0]a-1.
Repport dans l'équation différentielle :

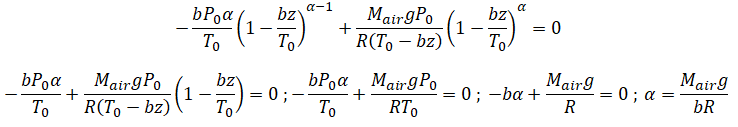On prendra a = 5,8.
10. En déduire l'expression littérale de µair(z).

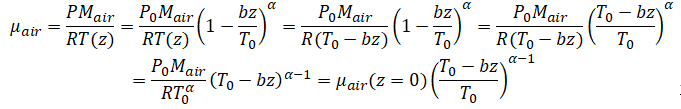Modélisation de la basse stratosphère.
Les basses couches sont caractérisées par une température constante T1 = 217 K.
11. Montrer que la pression de l'air est solution de  : dP / dz + P / H =0 où H est une constante à expliciter en fonction de Mair, R T1 et g.
dP/dz +µair(z) g=0
P = RT1 µair(z) / Mair  ; µair(z) =P Mair  / (RT1) ;
dP/dz +P Mair  g / (RT1) =0.
H = RT1 / ( Mair  g) .
12. Résoudre cette équation différentielle pour obtenir P en fonction de z, z1=12 km, P1 =P(z1) et de H.
P = A exp(-z /H) avec A une constante.
P1 = A exp(-z1 /H) ; A =P1 exp(z1 /H).
P =P1 exp((z1-z )/H).
13. Préciser la dimension et la signification physique de H.

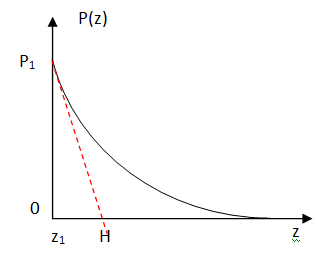
H est la hauteur caractéristique de la diminution de P(z).
14. En déduire l'expression de µair (z) dans la basse stratosphère en fonction de z, z1, P1, T1, Mair, R et H.
µair(z) = Mair P(z) / (RT1) =Mair P1 / (RT1) exp((z1-z )/H).

...
....

 Plafond atteint par la sonde.
Au début de la phase de montée, on considère que la masse d'hélium contenue dans le ballon est constante. L'équilibre thermique est assuré entre l'air extérieur et l'hélium à chaque instant.
15. Montrer que le volume du ballon s'écrit :
V(z) = mHe Mair / (MHe µair(z)).
V(z) =mHe / µHe  ;
or µHe / µair = MHe / Mair.
V(z) =mHe Mair./ (MHe µair(z)).
16. Comment évolue V(z) avec l'altitude ?
mHe Mair./ MHe est constant.
V(z) = constante / µair(z).
Or µair(z) diminue avec l'altitude ; V(z) augmente avec l'altitude.
17. Montrer que le ballon n'atteint pas son volume maximal dans la troposphère.

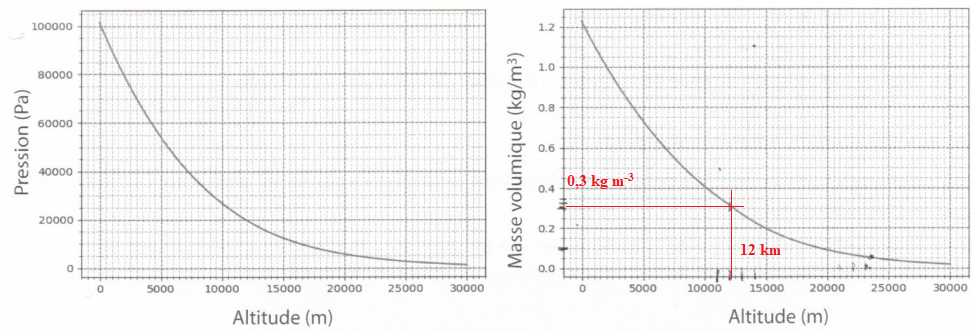
V(z) =mHe Mair./ (MHe µair(z))=1,83 103 x 29,0 / (4,00 x0,30)=4,4 104 m3 < 19,6 104 m3 = Vmax.
18. A quelle altitude z2, Vmax est-il atteint ?
V(z2) =Vmax=mHe Mair./ (MHe µair(z2)).
µair(z2))=mHe Mair./ (MHe Vmax)=1,83 103 x 29,0 / (4,00 x19,6 104)=6,8 10-2 kg m-3.
Le graphe ci-dessus conduit à z2 = 22 000 m ( basse stratosphère).
19. Comparer le poids et la poussée d'Archimède à l'altitude z2.
Poussée = µair(z2) V(z) g =6,8 10-2 x 19,6 104 g =1,3 104g.
Poids = (mHe +mballon) g = ( 1,83 103+1,20 103 ) g=2,0 103 g ( 5 fois plus faible que la poussée : la ballon monte plus vite).
Pour la suite du mouvement, le volume du ballon reste égal à Vmax et de l'hélium s'échappe via les manches d'évacuation. Le ballon atteint une position d'équilibre à l'altitude zmax.
20. Etablir l'expression littérale de µair(zmax) en fonction de mballon, Mair, MHe, Vmax. Faire l'application numérique.
 (m'He +mballon) g = µair(zmax) Vmax g.
m'He +mballon = µair(zmax) Vmax .
Or Vmax=m'He Mair./ (MHe µair(zmax)).
m'He =VmaxMHe µair(zmax) /  Mair.
m'He /Vmax =MHe µair(zmax) /  Mair.
µair(zmax)=(m'He +mballon) / Vmax =MHe µair(zmax) /  Mair+ mballon / Vmax .
µair(zmax)-MHe µair(zmax) /  Mair = mballon / Vmax
µair(zmax)[ 1-MHe /  Mair ]= mballon / Vmax .
µair(zmax) =mballon / [ Vmax (1-MHe /  Mair ) ].
µair(zmax)=1,20 103 / (1,96 105(1-4,0 / 29)]=7,1 10-3 kg m-3.
21. Déduire du graphe suivant l'altitude maxuimale de  vol.

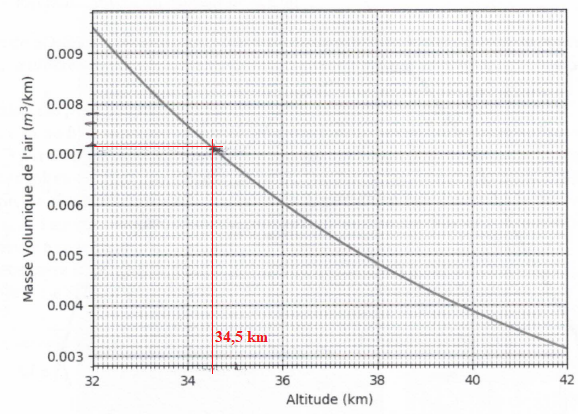
Zmax mesurée = 34,25 km ±0,20 km. Les deux valeurs sont en accord.
Vitesse de croisière dans la troposphère.

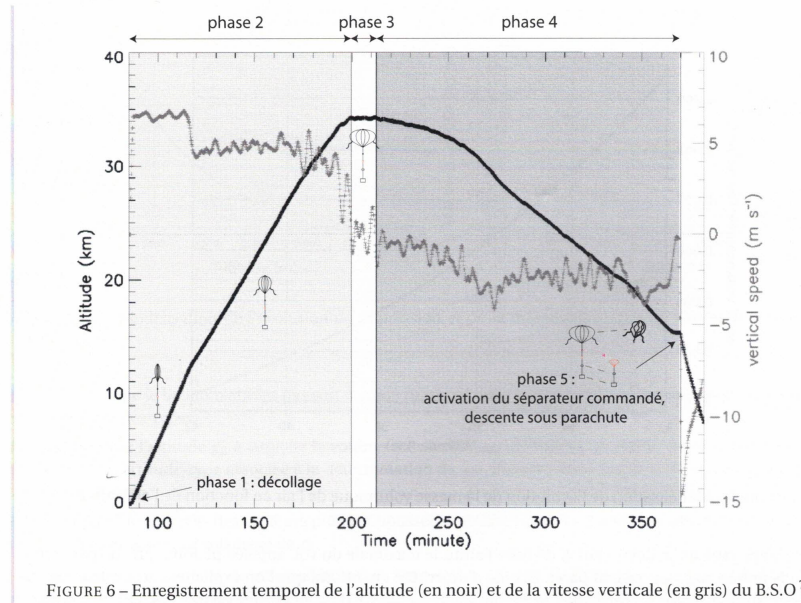
22. Caractériser le mpuvement du ballon dans la phase 2, dans la troposphère ( altitude 0 à 12 km).
Le graphe est un segment de droite ; la vitesse est à peu près constante voisine de 12000 / (30x60)~ 6,6 m/s .
Le ballon s'élève du fait de la poussée d'Archimède ; il subit une force de frottement proportionnelle au carré de la vitesse f = k(z) v2.
23. Faire le bilan des forces appliquées au ballon et justifier que le ballon va atteindre une vitesse limite.

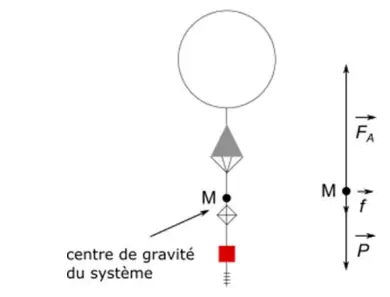
Le ballon est soumis à son poids, à la poussée d'Archimède et à la force de frottement.
La seconde loi de Newton écrite sur un axe vertical ascendant donne  en possant m = mballon + mhélium :
-mg -f +FA =m dv /dt.
m dv /dt+kv2-µair Vg= -mg.
Au cours de la montée, la vitesse augmente : le poids et la force de frottement vont finir par compenser la poussée d'Archimède. La vitesse limite sera alors atteinte.
24. Etablir l'expression de la vitesse limite.
dvlim /dt = 0 ; kv2lim =(µair V-m)g.
vlim = [(µair V-m)g / k]½.
Or V = mHe / µHe =mHe/ µairMair / MHe ;  v2lim = [(mHe Mair / MHe-mg ) / k].
vlim =[(mHe Mair / MHe-mg ) / k]½.
25. Calculer vlim si k = 2,05 103 SI.
vlim = [(1,23 103 x29 / 4-(1,83 103 +1,20 103)x9,8 / (2,05 103]½ ~ 7,0 m /s.
La vitesse mesure vaut 6,90 ±0,23 m/s.
26. Comparer ces deux valeurs.
La vitesse calculée appartient à l'intervalle [6,90 -0,23 ; 6,90 +0,23) soit [6,67 ; 7,13 ].
Accord entre les valeurs, le modèle proposé est valide.

  
menu