Emission
de SO2(g) stratosphérique suite à l'éruption d'un volcan,
concours
général
2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
L'éruption
volcanique du Mont Tambora a commencé le 5 avril 1815. La première
phase éruptive est associée à un volume éjecté, en équivalent solide,
de 11 ±2 km 3. Le volume total éjecté, en équivalent solide, est estimé à 41 ±4 km 3.
51. Une relation utilise le volume éjecté pour évaluer la hauteur H du panache ( km).
H = 25,9 log (V).
Estimer la hauteur du panache formé lors de la première phase éruptive. Nommer la couche atmosphérique atteinte par ce panache.
H = 25,9 log(11) ~27 km ().( Stratosphère).
Le panache du volcan injecte une quantité importante de gaz, dont SO 2(g)
et de poussières dans l'atmosphère. Les poussières retombent très vite.
Le dioxyde de soufre s'oxyde en acide sulfurique en environ 1 mois.
H 2SO 4 aq + H 2O(l) --> SO 42-aq + 2H 3O +aq.
55 10 6 tonnes de SO 2(g) ont été injectés à cette altitude H.
52. Comparer cet apport en espèces soufrées aux quantités habituelles présentes hors épisode volcanique.
Troposphère : sulfates 0,7 Gt ; SO2 : 0,5 Gt.
Stratosphère : sulfate 0,5 Gt.
n( SO2) : 55 1012 / M(SO2) =55 1012 / 64 =8,6 1011 mol.
m(sulfate ) =8,6 1011 M(sulfate) =8,6 1011 x96 =8,3 1013 g =0,083 Gt.
Soit une augmentation d'environ : 0,083 x100 / 0,5~ 17 %.
Effet sur le climat.
On suppose que le flux solaire incident de puissance surfacique moyenne Fs =341 W m-2 arrive perpendiculairement à la couche d'aérosols. Une partie de ce rayonnement traverse directement cette couche Ft = Fs e-d où d
est l'épaisseur optique caractéristique de la couche. Le reste du
rayonnement est diffusé, soit vers les basses couches et sera noté Fd soit vers l'espace. Il est noté Fu. On note ß la fraction du rayonnement diffusé qui repart vers l'espace.
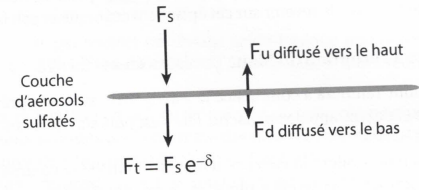
53. Traduire la conservation du rayonnement solaire incident.
Fs = Ft +Fd+Fu.
54. Montrer que Fu =Fsß(1- e-d) et Fd =(1-ß)Fs(1- e-d).
Fu = ß(Fs-Ft)=ß(Fs-Fs e-d) =Fsß(1- e-d).
Fd = (1-ß)(Fs-Ft)=(1-ß)(Fs-Fs e-d)=(1-ß)Fs(1- e-d).
55. On définit l'albédo de la couche d'aérosols sulfatés comme le rapport du flux repartant vers l'espace sur le flux incident.
A* =F u / F s. Exprimer A* en fonction de ß et d. A*= ß(1- e-d).
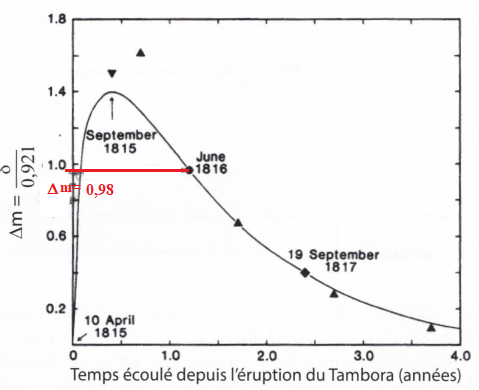
56. Estimer A* pour l'été 1816 sachant que ß =0,17.
d = 0,921 Dm =0,921 x 0,98 =0,903.
A* =ß(1- e-d)=0,17 (1-e-0,903)= 0,10.
57.
Exprimer Fu en fonction de A* et Fs. Exprimer Fs e-d+Fd en fonction de A* et Fs.
A* =Fu / Fs ; Fu = A* Fs.
A*/ ß =1- e-d ; e-d =1-A*/ ß.
Fs e-d+Fd = Fs( 1-A*/ ß)+(1-ß)FsA*/ ß.
Fs e-d+Fd = Fs [1-A*/ ß+A*/ ß-A*]=Fs (1-A*).
58. Evaluer la proportion du flux solaire incident traversant la couche d'aérosols et repartant vers le sol.
1-A* = 1-0,10 = 0,90.
Albédo terrestre en présennce d'une éruption volcanique majeure.
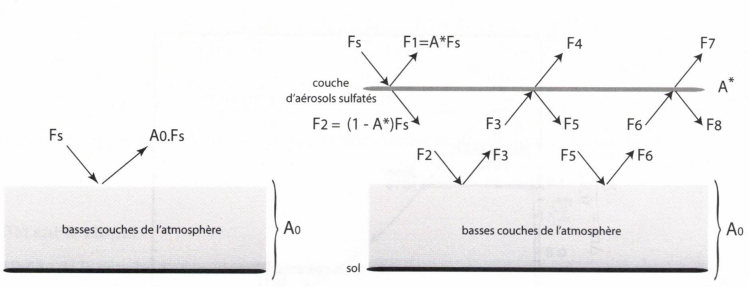
59. Exprimer les flux F3, F4, F5, F6, F7 et F8 en fonction de Fs, A0 et A*.
F3=A0 F2 =A0 (1-A*)Fs.
F5 = A* F3 =A*A0 (1-A*)Fs.
F4 = (1-A*)F3 =(1-A*)A0 (1-A*)Fs= (1-A*)2A0Fs.
F6=A0 F5 =A*A02 (1-A*)Fs.
F7 =(1-A*)F6=A*A02 (1-A*)2Fs.
F8=A* F6=A*2A02 (1-A*)Fs.
60. On définit l'albédo total AT
vu de puis un satellite scrutant la terre en présence de la
couche d'aérosols, comme le rapport de tous les flux repartant vers
l'espace, sur le flux solaire incident.
AT = (F1+F4+F7) / Fs =A* +(1-A*)2A0 +A*A02 (1-A*)2.
61. Un calcul prenant en compte l'ensemble des réflexions successives donne :
AT = A* +(1-A*)2A0 / (1-A0A*).
Calculer AT.
AT =0,10 + 0,31 (1-0,10)2 / (1-0,31 x0,10)=0,36 > 0,31.
Une plus grande partie du rayonnement solaire repart vers l'espace en
présence d'une couche d'aérosols : d'où un refroidissement.
|
...
|
....
|
Effet de forçage radiatif associé à la présence de la couche d'aérosols.
En
absence de la couche d'aérosols, la puissance non réfléchie par la
couche d'albédo est absorbée par la terre, qui se comporte comme un
corps chaud de température uniforme TT
émettant un rayonnement infrarouge en direction de l'atmosphère.
l'atmosphère absorbe une fraction f de ce rayonnement. Elle ré-émet à
son tour un rayonnement infrarouge identique en direction de l'espace
et de la terre. La surface de la terre absorbe à son tour tout
rayonnement infrarouge provenant de l'atmosphère. l'ensemble du
rayonnement infrarouge visible par un satellite qui pointerait en
direction de la terre vaut (1-0,5 f)s TT4.
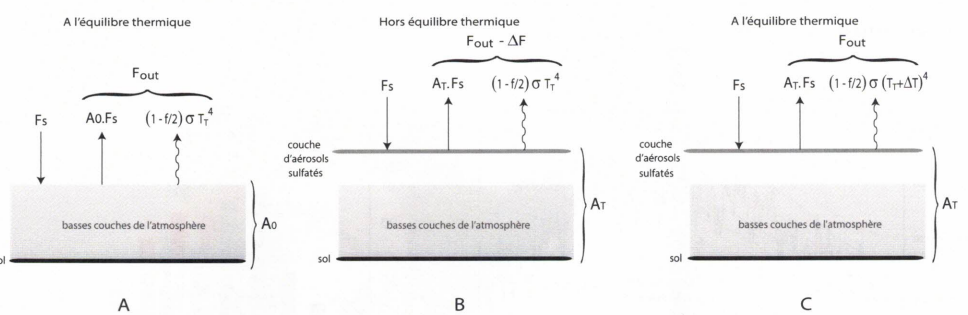
62. Evaluer f à l'équilibre thermique en absence de couche d'aérosols.
s = 5,67 10-8 S I ; TT = 288 K.
Fs = A0Fs + (1-0,5 f)s TT4.
1-0,5 f =(1-A0) Fs / (s TT4) ;
f = 2 [1-(1-A0) Fs / (s (TT4)].
f = 2 [1-(1-0,31) 341 /(5,67 10-8 x2884)] ~0,79.
A la suite d'une éruption volcanique AT = 0,36. Un
déséquilibre thermique apparaît. On suppose dans un premier temps que
la température de la surface de la terre n'a pas eu le temps d'évoluer.
On suppose également que f garde la même valeur.
63. Exprimer DF puis le calculer ( schéma B).
Fout - DF =ATFs + (1-0,5 f)s TT4.
De plus : Fout =A0Fs + (1-0,5 f)s TT4.
DF =(A0-AT)Fs =(0,31-0,36) x341 = -17 W m-2.
L'atmosphère perd de l'énergie et se refroidit.
64. Si le forçage radiatif dure assez longtemps, un nouvel équilibre thermique est atteint ( schéma C). On note TT+ DT la nouvelle température de la surface de la terre. Montrer que DT = DF /(4(1-0,5 f)s TT3).
Si DT << TT, (TT+DT)4 ~TT4+4TT3DT.
Fout =ATFs + (1-0,5 f)s (TT+DT)4 ~ATFs + (1-0,5 f)s (TT4+4TT3DT).
De plus : Fout =A0Fs + (1-0,5 f)s TT4.
(AT-A0)Fs +(1-0,5 f)s 4TT3DT =0.
DT =(A0-AT)Fs / [(1-0,5 f)s 4TT3 ] = DF /(4(1-0,5 f)s TT3)
65. Evaluer DT.
DT = -17 / [4(1-0,79 x0,5)x2883 x5,67 10-8]= -5,2°C.
|
|