Mathématiques,
concours
Police Technique et Scientifique 2022.
( zone Nord)
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Pour chaque question, cocher ou entourer la (ou les) réponse(s) correcte(s)
Question
1 : −x2+ 14x−49 est égal à :
A. -(x-7)2 vrai ; B. (7-x)2 ; C. (-x-7)2 ; D. (-7+x)2 .
−x2+ 14x−49= -(x2-14x+72)=-(x-7)2.
Question 2 : 2. (2x+ 4)2 −(3x−2)2 est égal à :
A. −5x2+ 12 ; B. −5x2+ 20 ; C. (−x+ 6)(5x−2) ; D. (−x+ 6)(5x+ 2) vtrai.
[(2x+4)-(3x-2)][(2x+4)+(3x-2)]= (-x+6)(5x+2).
Question 3 :(x3−1)2 est égal à :
A. x6−2x3+ 1 vrai ; B. x9−2x3+ 1 ; C. x2−3x3+ 6 ; D. 6-3x -x2.
Question 4 : Dans tout ce qui suit, a désigne un réel quelconque.
Si f(x) tend vers 3 quand x tend vers a alors :
A. La limite de 1/ f(x) est égale à 0 quand x tend vers a.
B. La limite de 1/ f(x) est égale à +oo quand x tend vers a.
C. La limite de 1/ f(x) est égale à 1/3 quand x tend vers a. Vrai.
Question
5 : Si f(x) tend vers -oo quand x tend vers a alors :
A. La limite de 1/ f(x) est égale à 0 quand x tend vers a. Vrai
B. La limite de 1/ f(x) est égale à +oo quand x tend vers a.
C. La limite de 1/ f(x) est égale à -oo quand x tend vers a.
Question 6 :
Si f(x) tend vers -3 et si la limite de g(x) est égale à +oo quand x tend vers a alors :
A. La limite de g(x) f(x) est égale à -3 quand x tend vers a.
B. La limite de g(x) f(x) est égale à -3 quand x tend vers +oo.
C. La limite de g(x) f(x) est égale à -3 quand x tend ver-ooa.
Par produit des limites, g(x) f(x)tend vers -oo.
Question 7 : La fonction définie par f(x) = 2x+ 5 admet pour dérivée la fonction f′ définie par :
A f '(x) = x2+5x ; B. f '(x) =2x ; C. f '(x) =2+5 ; D. f '(x) = 2 vrai.
Question 8. On définit la fonction f sur ]2,5 ;+∞[ par : f(x)=(3x+1) / (−2𝑥+5)
f ′(x) est donné par l’expression :
A. -2x+5 ; B. 17 / (-2x+5)2 vrai ; C. 13 / (-2x+5)2 ; D.-13 / (-2x+5)2 .
On pose u = 3x+1 et v = -2x+5.
u' = 3 ; v' = -2.
(u'v-v'u) / v2 =[3(-2x+5)+2(3x+1)] /((-2x+5)2 =17 / (-2x+5)2 .
Question 9 : On considère la fonction g définie sur ℝ par g(x)=2x2+5x−4.
La tangente à la courbe représentative de g au point d’abscisse 2 a pour équation :
A. y = 14 x+14 ; B. y = 14 x-14 ; C. y = 13 x-15 ; D. y = 13x-12. Vrai.
g' = 4x+5 ; g'(2) = 13, coefficient directeur de la tangente.
Le point de coordonnées (2 ; g(2)=14) appartient à la tangente.
Equation de la tangente y = 13 x+b ; 14 = 13*2+b ; b = -12.
|
...
|
....
|
Question 10 : Le plan est rapporté à un repère orthonormé. On considère les points G(1 ;−2) et H(6 ;4). La droite (GH) passe par
le point :
A(-3 ; 2) ; B. (2,5 ; 0) ; C(10 ; 12) ; D (-14 ; -20) vrai.
Equation de la droite (GH) : y = ax +b.
G appartient à cette droite : -2 = a+b.(1)
H appartient à cette droite : 4 = 6a+b.(2).
(2)-(1) donne : 6=5a ; a = 6/5 = 1,2 : par suite b = -2-a = -3,2.
y =1,2x-3,2.
Si A appartient à cette droite : 1,2 *(-3)-3,2 = 0,4 diffère de 2.
Si B appartient à cette droite : 1,2 *(2,5)-3,2 = -0,2 diffère de 0.
Si C appartient à cette droite : 1,2 *(10)-3,2 = 8,8 diffère de 12.
Si D appartient à cette droite : 1,2 *(-14)-3,2 = -20.
Question 11 :Parmi les propositions suivantes quelles sont celles qui sont correctes ?
A. ex+y = ex+ey.
B. ex+y = ex.ey. Vrai.
C. ex.y = ex+ey.
D. ex.y = ex.ey.
Question 12 : Pour tout réel 𝑥, l’expression ex .ex+2 est égale à :
A. e2x+2. Vrai.
B. exp(x2+2)
C. exp(x / (x+2).
D. exp(x2+2x).
Question 13 : Parmi les propositions suivantes quelles sont celles qui sont correctes ?
A.ln(a+b) = ln(a) . ln(b). Vrai.
B. ln(ab) = ln(a). ln(b).
C. ln(a / b) = ln(a) - ln(b). Vrai.
Question 14 : ln(x2 ) est égal à :
A. (ln(x))2. B. 2 ln|x|. vrai C. 2 ln(x). D. x ln(2).
Si x >0 ; ln(x2 ) =2 ln(x).
Question 15 : Dans le plan muni d’un repère, on considère la droite (AB) passant par les points A(−2 ; 7) et B(4 ;−5) Un vecteur
directeur de la droite (AB) a pour coordonnées :
A. (2 ; 2) ; B. (-12 ; 6) ; C. (6 ;-12) vrai ; D. (2 ; -12).
Coordonnées du vecteur AB : 4-(-2) ; -5 -7 soit 6 ; -12.
Coordonnées d'un vecteur directeur de la droite (AB) : k ; -2k avec k réel.
Question 16 : (un) désigne une suite arithmétique de raison a et de terme initial u0.
Si u1=5 et que a =– 2 alors u8= ?
A. -11 ; B. -9 vrai ; C. 19 ; D. 40.
u2 = 5-2 = 3 ; u3 = 3-2=1 ; u4 = 1-2 = -1 ; u5 = -1-2=-3 ; u6 = -3-2 = -5 ; u7 = -5-2=-7 ; u8 = -7-2 = -9.
ou bien u8 = u1+7a = 5+7(-2) = -9.
Question 17 : (un) désigne une suite géométrique de raison b et de terme initial u0 Si u0=1/2 et que u1=4 alors b = ?
A. 2 : B. 8 vrai ; C. 3,5 ; D. 4.
u1 = u0 b ; b = 4 / 0,5 = 8.
Question 18 : La suite (un) définie par un=5×2n.
A. Est une suite géométrique de premier terme u0=2 et de raison 555
B. Est une suite géométrique de premier terme u0=5 et de raison 2. Vrai.
C. N'est pas une suite géométrique.
D. Est une suite arithmétique.
Question 19. On lance deux dés non truqués. Quelle est la probabilité de n'obtenir aucun 6 ?
A. 1 / 36 ; B. 11 / 36 ; C. 25 / 36. Vrai. D. 35 / 36.
11 cas favorables : (6 ; 1) ; (6 ; 2) ; (6 ; 3) ; (6 ; 4) ; (6 ; 5 ) ;
(6 ; 6) ; (1 ; 6) ; (2 ; 6) ; (3 ; 6) ; (4 ; 6) ; (5 ; 6 ) .
Probabilité de n'obtenir aucun 6 : (36-11) / 36 = 25 / 36.
Obtenir aucun 6 : 1 -2 /36 = 34 / 36.
Question 20. On lance deux dés non truqués. Quelle est la probabilité d'obtenir au moins un 6 ?
A. 1 / 36 ; B. 11 / 36 Vrai ; C. 25 / 36. D. 35 / 36.
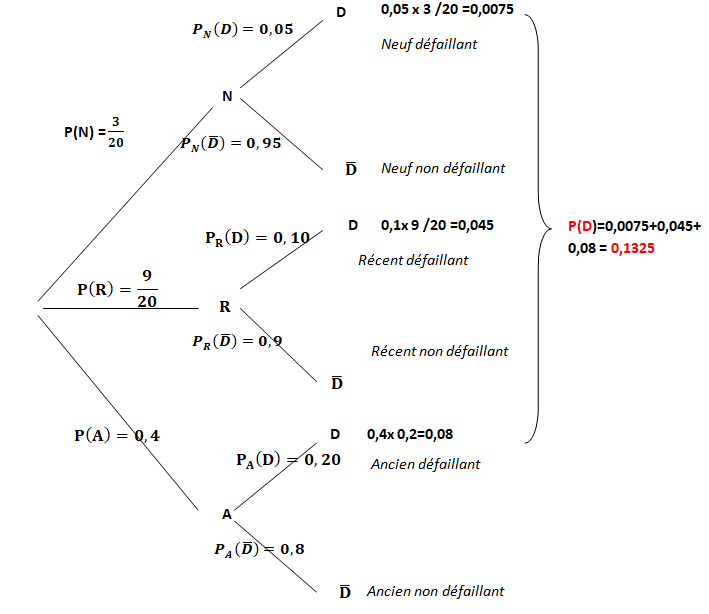
Le parc informatique du laboratoire de police scientifique de Lille est composé de 200 ordinateurs dont :
• 30 sont considérés comme neufs ;
• 90 sont considérés comme récents ;
• les autres sont considérés comme anciens.
Une étude statistique indique que :
• 5 % des ordinateurs neufs sont défaillants ;
• 10 % des ordinateurs récents sont défaillants ;
• 20 % des ordinateurs anciens sont défaillants.
On choisit au hasard un ordinateur de ce parc.
On note les événements suivants :
• N : « L'ordinateur est neuf » ;
• R : « L'ordinateur est récent » ;
• A : « L'ordinateur est ancien » ;
• D : « L'ordinateur est défaillant » ;
• D‾ : l'événement contraire de D.
1. Construire un arbre pondéré décrivant la situation.
2. Calculer la probabilité que l'ordinateur choisi soit neuf et défaillant.
3. Démontrer que la probabilité que l'ordinateur choisi soit défaillant est égale à 0,1325.
4.
Déterminer la probabilité que l'ordinateur soit ancien sachant qu'il
est défaillant. Donner le résultat sous forme décimale arrondie au
centième.
PD(A) =P(D n A) / P(D) =0,08 / 0,1325~0,60.
|
|