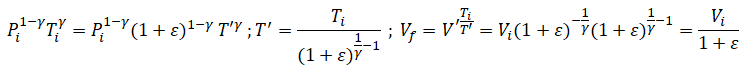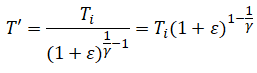Une quantité de n moles de diazote, gaz supposé parfait, subit, successivement, les transformations thermodynamiques
suivantes :
- T
1 : une transformation adiabatique réversible de l’état initial E
i
(température T
i
, pression P
i
, volume V
i) à l’état E
′
(température T
′
, pression P
i
(1 +
e)), volume v' ;
- T
2 : une transformation isobare de l’état E
′
à l’état final E
f (température T
f = T
i
, pression P
f, volume V
f).
𝑅 ≈ 8 J. K
−1
. mol
−1
la constante des gaz parfaits.
1. Quelles sont, en fonction de Vi
,
e et
g, les expressions de V
′
et de V
f ?
Transformation T1 : loi de Laplace : Pi Vig = Pi (1+e) V 'g ;
V ' =Vi /(1+e)1/g =Vi (1+e)-1/g . Réponse A.
Transformation T2 :V' / T' = nR / Pf = Vf / Tf = Vf / Ti.
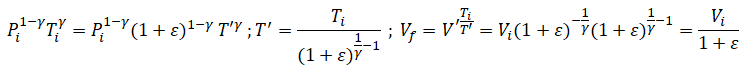
Réponse D.
2. . Donner l’expression de T
′
en fonction de T
,
e et g,
D'après la question précédente :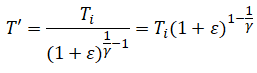 
Réponse B.
3. Déterminer le travail (algébrique) W
EiE' reçu par le gaz au cours de la transformation T
1.
T
1 est adiabatique :
WEiE' =DUEiE'= n Cv (T '-Ti)=n Cv Ti (T '/Ti -1)
Relation de Mayer : Cp-Cv=nR ; g = Cp / Cv ; Cv = nR / (g-1).
WEiE' = nRTi / (g-1)(T '/Ti -1)=PiVi / (g-1) [(1+e)1-1/g -1].
Réponse C.
4. Déterminer le travail (algébrique) WEiEf reçu par le gaz au cours de la transformation T2.
La transformation étant isobare :
WEiEf = -Pf (Vf-V') = - Pf Vf [1-V' / Vf] = -Pf Vf [1-T' /Ti].
WEiEf = - Pi (1+e) Vi / (1+e) [1-(1+e)1-1/g].
WEiEf = -Pi Vi [1-(1+e)1-1/g]. Réponse C.
5. Après avoir donné l’expression du bilan d’énergie interne DU entre les états Ei et Ef, déterminer la chaleur, ou transfert
thermique (algébrique), Q, reçue par le gaz au cours de la série de transformations qui l’amène de Ei à Ef.
Ti = Tf, l'énergie internez d'un gaz parfait ne dépend que de la température : DU = 0. Réponse A.
Q = -WEiE' -WEiEf = -PiVi / (g-1) [(1+e)1-1/g -1] +Pi Vi [1-(1+e)1-1/g].
Q = Pi Vi [1-(1+e)1-1/g] g / (g-1). Réponse C.
6. Que deviennent les expressions du travail total W = W
EiE' +
WEiEf
et de Q si
e ≪ 1 ?
Développement limité à l'ordre 1 de
(1+e)1-1/g ~1+e-e/g.
1-(1+e)1-1/g ~e-e/g = e(1-1/g).
W = -Q = Pi Vi g / (g-1)[e(1-1/g) ] = Pi Vi e . Réponses B et D.