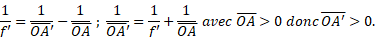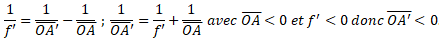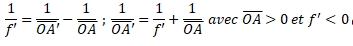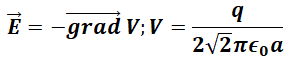Partie III.
Un point M a pour coordonnées M(x, y, z). Un carré, de sommets A, B, C, D a pour centre O et pour côté 2a.
A chaque sommet sont placés des particules identiques de charge q.
Q19. Le champ électrique en O est nul. Réponse A.
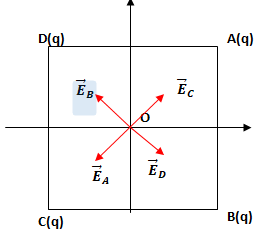
Q20. Le potentiel électrique en O a pour expression.
V(O) = constante différente de zéro. L'origine des potentiels est choisie à l'infini.
Q21.
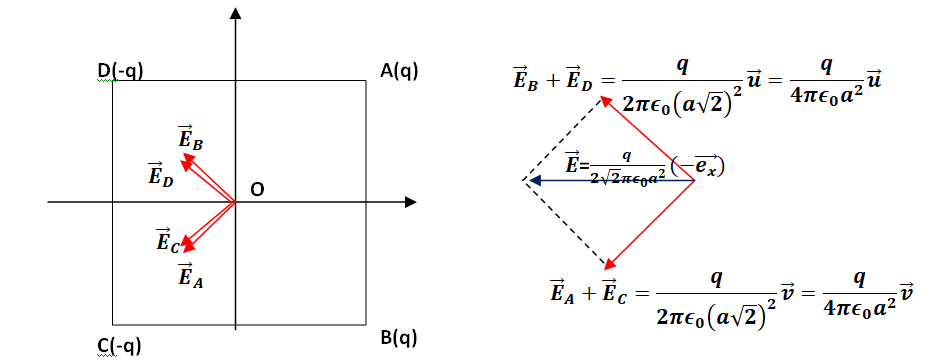
Réponse C.
Q22. Le potentiel électrique en O a pour expression :
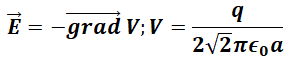
Réponse E.
Réponse D.
Q23.
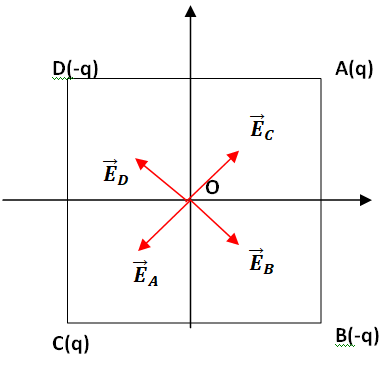
Le champ électrique en O est nul. Réponse A.
Q24. Le potentiel électrique en O est constant différent de zéro. L'origine des potentiels est choisie à l'infini..
Q25. La permittivité électrique du vide e0 a pour unité : F m-1. Réponse D.
Q26. L'ordre de grandeur de e0 dans le système internationnal est 10-11. Réponse A.
Partie IV.
Un cylindre infini d'axe Oz et de rayon R est chargé uniformément en volume. On note r0 sa charge volumique.
On se place en régime stationnaire.
Un point M de l'espace esr repéré par les coordonnées cylindriques ( r, q, z).
Q27. Les équations de Maxwell qui régissent l'électrostatique sont :
L'équation de Maxwell-Gauss et l'équation de Maxwell-Ampère. Réponses B et D.
Q28. Le champ électrique est contenu dans les plans de symétrie pour les charges. Réponse A.
Un plan perpendiculaire à l'axe du cylindre est plan de symétrie pour
la distribution de charges. Le champ électrique appartient à ce plan.
Il y a invariance de la distribution de charges :
- par translation selon l'axe Oz : E ne dépend pas de z.
- par rotation autour de l'axe Oz : E ne dépend pas de q.
Les équipotentielles sont perpendiculaires au champ électrique, donc des cylindres. Réponse C.
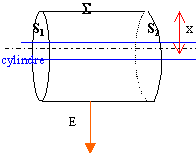
Q29. Pour r < R le champ électrique en M s'écrit :
flux
de E à travers S.
En tout point de la surface
latérale
S, par raison de
symètrie, le champ est radial et a même module.
Le flux de ce vecteur à travers la surface
latérale de longueur h
est E
2pxh.
En tout point de S1 ou
S2 le vecteur E est normale au vecteur surface :
le flux de E est nul à travers les 2
bases.
charge intérieure au cylindre S
de rayon x :
x < r :
Q=px²hr.
x > r :
Q=pr²hr.
th
de Gauss :
E
2prh
= Q/e0.
x < r : E=
xr
/
(2e0) Réponse
B.
x > r :
E=
r²r
/
(2e0x)
Q30. Pour r > R le champ électrique est : réponse C.
Q31.Le potentiel électrique en M est noté V(r). On choisit l'origine des potentiel en r = R. Pour r < R il s'écrit :
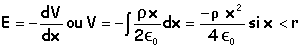
V(R) =0 =-rR2/ (4e0) +Cste ; Cste = rR2/ (4e0). Réponse A.
Q32. Pour r > R, V(M) s'écrit :
si x > R : V =
-R²r
/ (2e0) ln(x) +
Cte.
V(R) =0 =-rR2/ (2e0) ln(R)+Cste ; Cste = rR2/ (2e0).ln(R). Réponse C.
Partie V.
Un fil cylindrique infini d'axe Oz et de rayon R est parcouru par un
courant I réparti uniformément en volume. On se place en régime
stationnaire.
Un point M de l'espace esr repéré par les coordonnées cylindriques ( r, q, z).
Q33. Le champ magnétique est :
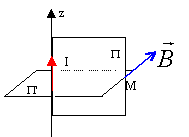
plan P : plan de
symétrie pour le courant ; le champ magnétique
en M est perpendiculaire à ce plan.
l plan P' : plan
d'antisymétrie pour le courant : le champ
magnétique en M est contenu dans ce plan.
le champ magnétique en M est
orthoradial. Réponse B.
Les lignes de champ créées par ce fil sont des cercles. Réponse C.
Q34. Les équations de Maxwell qui régissent la magnétostatique sont :
L'équation de Maxwell-Faraday et l'équation de Maxwell-Thomson. Réponses A et C.
Q36. Pour r > R le champ magnétique en M s'écrit :
La norme du champ magnétique
en Mse calcule à l'aide du théorème
d'Ampère
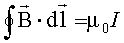
On calcule la circulation sur un
cercle: le champ est constant sur ce contour et reste
tangent au cercle.
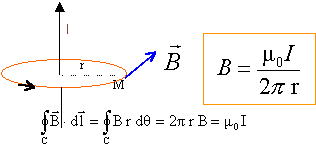 Réponse B. Réponse B.
Q35. Pour r < R le champ magnétique en M s'écrit :
Remplacer I par I(r / R)2 dans l'expression précédente. Réponse C.
Q37. La perméabilité magnétique du vide µ0 a pour unité : H m-1. Réponse D.
Q38. L'ordre de grandeur de µ0 dans le système internationnal est 10-6. Réponse C.
Partie VI. Filtre linéaire.
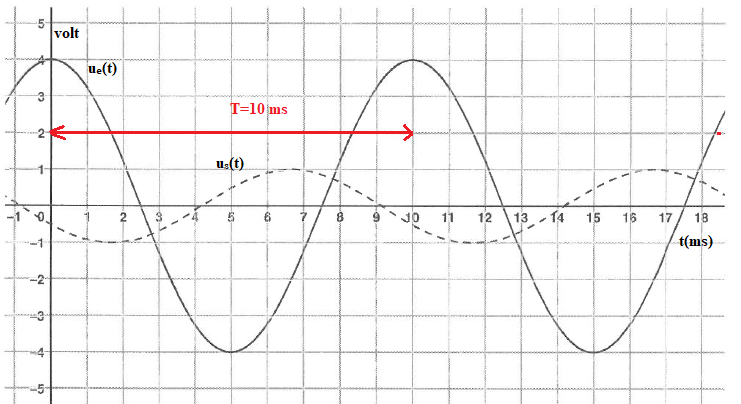
Q39. Le signal d'entrée a pour fréquence :1 /T = 1 /0,01 = 100 Hz. Réponse B.
Son amplitude est 4 V. Réponse C.
Q40. ue(t) a pour valeur efficace : 4 /2½ = 2 *2½ volts. Réponse B.
Q41. Le déphasage de us(t) par rapport à ue(t) vaut :
us(t) est en avance de 3,5 carreaux soit 3,5 / 10 =0,35 T ou 0,35 x180 ~60 °. Réponse A.
Un autre filtre linéaire, de fonction de transfert H donne les chronogrammes ci-dessous. donne :
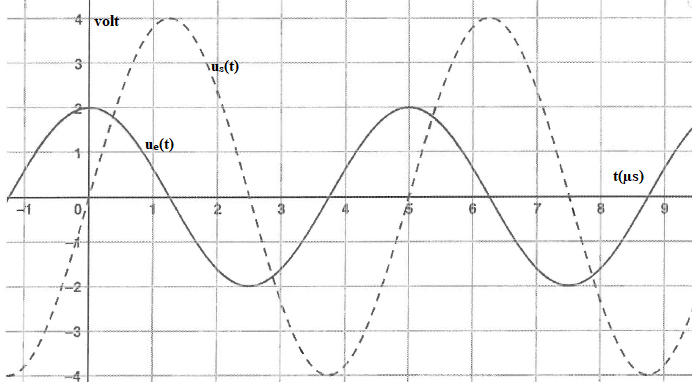
Q42. La fonction de transfert a pour module |H| = 4 / 2=2. Réponse 2.
et pour argument p/2 radian. Réponse D. ( us est en avance de p/2 sur ue).
Q43 La fonction de transfert s'écrit : H = 2 j. Réponse A.
R = 1 kW ; E = 15 V.

I1 = E / Réqui = 15 / 750 =0,02 A.
|