Physique, Concours ingénieur de l'industrie et des mines 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1.  1. Définir ce qu'est un champ en physique. Un champ est la donnée, en chaque point de l'espace-temps, de la valeur d'une grandeur physique, scalaire ou vectorielle. 2. Donner les ordre de grandeurs des champs magnétiques suivants : champ terrestre, champ produit par un aimant domestique de bonne qualité, champ utilisé en IRM. Champ terrestre : 50 µT ;  champ produit par un aimant domestique de bonne qualité : 0,1T ;  champ utilisé en IRM : 1 à 3 T. 3. Donner le schéma électrique équivalent et établir l'équation différentielle décrivant la dépendance temporelle du courant. 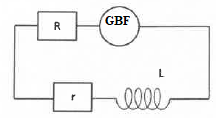4.Commenter par rapport au phénomène d'autoinduction et à la loi de Lenz. La bobine parcourue par le courant créé un champ magnétique qui créé un courant induit dans la bobine. Ce courant induit s'oppose à la cause qui lui donne naissance. Il a le sens inverse du courant initial.   5. 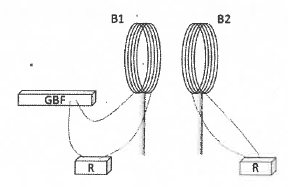Lorsque B1 est alimentée par un générateur délivrant des signaux sinusoidaux, une tension apparaît aux bornes de B2. Pourquoi ? Que se passeraît-il si B1 est alimenté en courant continu ? On considère deux solénoïdes S1 et S2 comportant respectivement N1 et N2 spires, de rayons respectifs R1 et R2 avec R2 < R1 mais très voisin de R1, de longueur l (l >> R1). Ces deux solénoïdes sont bobinés dans le même sens, ont même axe et le solénoïde S1 est obtenu en bobinant ses spires par dessus celles du solénoïde S2 sur toute la longueur l. Le solénoïde S1 est parcouru par un courant i, tandis que S2 est en court-circuit. 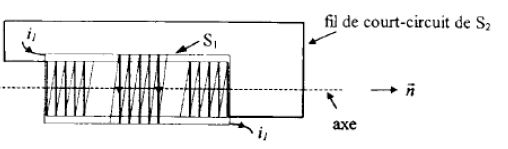Pour le calcul des flux, la normale n commune aux spires des deux solénoïdes est définie à partir du sens de i1. Déterminer le flux F1-->2 dû à B1, envoyé par S1 à travers les N2 spires de S2. B1 = µ0N1 i1/l ; F1-->2 =N2 B1 S2=N2  µ0N1 i1/l S2 = µ0N1N2 i1/l pR22. En déduire l'expression de la f.é.m induite dans le solénoïde S2 et le sens positif du courant induit i2 pour i1 croissant. e = -dF1-->2/dt = -µ0N1N2 /l pR22 di1/dt avec di1/dt positif. e est donc négative et i2 est de sens contraire à i1. On pose : F1-->2= M21 i1. On appelle mutuelle inductance le coefficient M21. Si B1 est alimenté en courant continu , le flux créé à travers la seconde bobine est constant : il n'y a donc pas de courant induit.   6. On note M l'inductance mutuelle d'un circuit sur l'autre. Donner le schéma électrique équivalent pour ces deux circuits ainsi que les équations différentielles déterminant la dépendance temporelle du courant dans chaque circuit. On note Ug(t) la tension aux bornes du générateur. 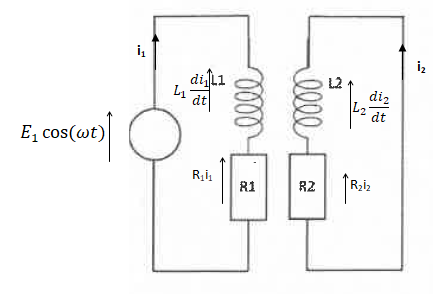Ug(t) = E1 cos (wt) =L1 di1/dt +R1i1+M di2/dt. L2 di2/dt +R2i2+M di1/dt = 0. 7. Exprimer le déphasage entre ces courants en utilisant la notation complexe. (R1 +jL1w)i1 +jMwi2 = E1. (R2 +jL2w)i2 +jMwi1=0. i2 =jMw / (R2 +jL2w ) i1=jMw (R2 -jL2w ) / (R22 +(L2w )2) i1 =( j MR2 w +ML2w2 ) / (R22 +(L2w )2) i1 . tan f = MR2 w / (ML2w2 ) = R2  / (L2w ). 8. Quelle est la valeur limite que peut atteindre le courant dans la seconde bobine ? i2 =jMw / (R2 +jL2w ) i1= jM / (R2 / w +jL2 ) i1. Quand w devient très grand et si R2 est faible : i2 = jM / (jL2 ) i1. Valeur limite de i2 = M / L2.   9. Citer 4 applications du phénomène d'induction dans l'industrie et dans la vie courante. Plaques à induction ; bande magnétique de stockage des données ; IRM ; train à lévitation magnétique ; freinage magnétique ; capteur de courant. ... .... Exercice 2. 1. Calculer la vitesse minimale d'une fusée ( assimilée à un point matériel ) devrait avoir pour s'échapper de l'attraction terrestre. 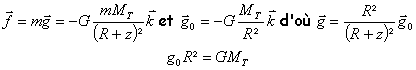Champ de pesanteur à l'altitude z La force de gravitation est conservative, l'énergie mécanique du corps se conserve au cours du mouvement. 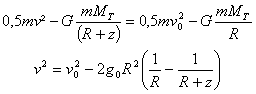Un corps M de masse m est lancé depuis la surface de la terre verticalement vers le haut avec une vitesse initiale v0. Son mouvement est rectiligne et sa position est repérée sur un axe vertical vers le haut, l'origine étant le centre de la terre. Si la vitesse de départ n'est pas suffisante, le corps atteint l'altitude zmax puis retombe. L'énergie mécanique est positive ou nulle , ce qui caractérise un corps pouvant s'échapper de l'attraction terrestre. 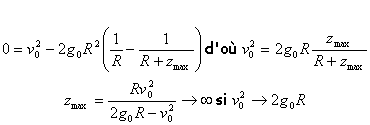application numérique : v0 = 11,2 km/s. 2. Quelle direction sur terre et direction du lancer permettent de maximiser la vitesse d'entrainement due à la rotation de la terre  et ainsi minimiser la vitesse par rapport au sol ? Evaluer l'économie d'énergie obtenue en lançant une fusée de Kourou ( 5° de latitude nord) par rapport à Cap Canaveral (28° N). Rterre = 6370 km. 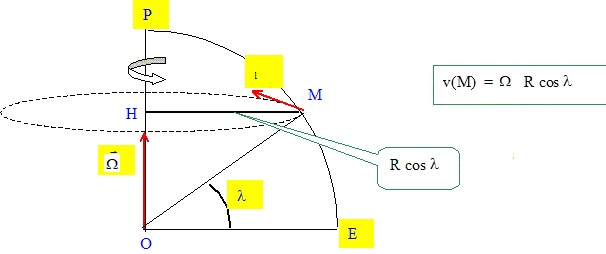Lancer vers l'est, la fusée se déplace dans la même direction que la rotation de la terre. Du fait de la rotation de la terre, la vitesse initiale de la fusée est maximale à l'équateur ( l = 0 et cos 0 = 1). Cette vitesse vient s'ajouter à celle imprimée par le lanceur. Jour sidéral TT = 23 h 56 min 4 s = 86164 s. La terre accomplit un tour sur elle même en 86164 s.  W = 2 x3,14 / 86164 ~7,29 10-5 rad s-1. A Kourou : v1 = 7,29 10-5 x6,37 106 x cos5 ~463 m /s. A Cap Canaveral : v2 = 7,29 10-5 x6,37 106 x cos28 ~410 m /s. Gain d'énergie cinétique : ½ M ( v12-v22) avec M masse de la fusée. 3. On considère un point se déplaçant à la vitesse v constante autour de la terre, à une altitude h. Durant le temps Dt le point se déplace le long de l'arc AB. Montrer que pour conserver une vitesse constante, l'accélération doit être égale à v2 / h. 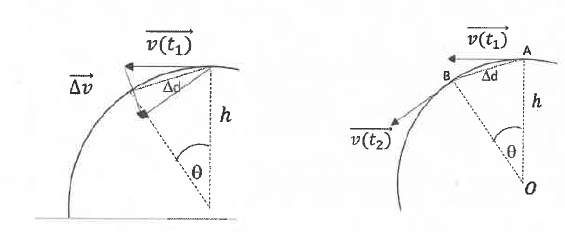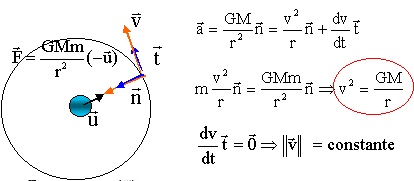La norme de la vitesse étant constante, l'accélération est centripète de norme v2 / h. 4. Calculer cette vitesse pour un satellite géostationnaire se trouvant à 6,6 Rterre du centre de la terre. Mterre = 5,97 1024 kg ; G = 6,7 10-11 S.I. v2 = GM / h =6,67 10-11 x5,97 1024 / (6,6 x6,37 106)=9,47 106 ; v ~3,1 103 m /s. 5. En assimilant la lune à un point tournant autour de la terre avec une période de révolution Tlune et la terre à un point tournant autour du soleil en Tterre, exprimer le rapport entre la masse du soleil et celle de la terre en fonction de Tlune, Tterre et des distances Terre-lune et Terre-soleil. Comment améliorer cette expression ? 3ème loi de Kepler : système terre lune : T2lune / d3 TL = 4p2 / (GMterre ). Mterre = 4p2 d3 TL / (GT2lune). système terre soleil : T2terre / d3 TS = 4p2 / (GMsoleil ). Msoleil = 4p2 d3 TS / (GT2terre). Msoleil  / Mterre =(dTS / dTL)3 (Tlune / Tterre)2.

menu