Chimie, Concours ingénieur de l'industrie et des mines 2023. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . .. .. ...... ... Exercice 1. Réchauffement climatique et acidification des océans. Les océans absorbent une proportion de dioxyde de carbone de l'atmosphère. Dans l'eau le dioxyde de carbone est sous forme dissoute ou hydratée  H2CO3 aq. H2CO3 aq / HCO3- aq. pKa1 = 6,4. HCO3- aq/ CO32-aq . pKa2 = 10,3.  1. Donner l'expression de Ka associé au couple acide / base AHaq / A-aq. En déduire le lien entre pKa et pH. AH aq + H2O l = A-aq + H3O+aq. Ka = [ A-aq] [ H3O+aq ] / [AH aq]. [ H3O+aq ] =Ka [AH aq] / [ A-aq]. log [ H3O+aq ] =log Ka +log ([AH aq] / [ A-aq]). -log [ H3O+aq ] = -log Ka -log ([AH aq] / [ A-aq]). pH = pKa +log ( [ A-aq] / [AH aq] ). 2. Tracer le diagramme de prédominance de l'acide carbonique. 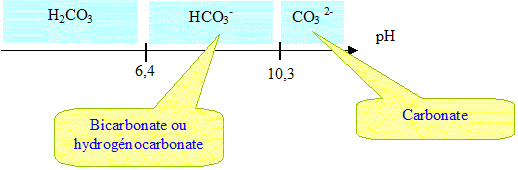3. Ecrire l'équation de la réaction de l'acide carbonique avec l'eau. Expliquer pourquoi l'augmentation de la concentration en CO2 de l'atmosphère entraîne l'acidification  des océans. CO2(aq) + 2H2O(l) = H3O+aq + HCO3-(1). HCO3-+ H2O(l) = H3O+aq + CO32-(2). L'augmentation du dioxyde de carbone dans l'atmosphère déplace l'équilibre CO2(g) = CO2(aq) dans le sens direct. CO2(aq) augmentant, l'équilibre (1) est déplacé dans le sens direct ; il en est de même pour l'équilibre (2). En conséquence la quantité d'ion oxonium H3O+aq croît et le pH de l'eau des océans diminue. Le pH des océans est aujourd'hui compris entre 8,1 et 8,3. Les scientifiques s'attendent à une diminution de ce pH de 0,3 dans 100 ans. Les coraux ont un squelette de carbonate de calcium CaCO3(s). Ks = 10-8,3 à 25°C. 4.a. Ecrire l'équation de dissolution du carbonate de calcium dans l'eau. CaCO3 (s) = Ca2+ (aq) + CO32- (aq). 4.b. Donner l'expression du produit de solubilité du carbonate de calcium. Ks = [Ca2+aq][CO32-aq]. Pour les trois questions suivantes, le pH sera compris entre 7,3 et 9,3. 4.c Justifier que la solubilité s du carbonate de calcium est s = [Ca2+] ~[HCO3- ]. A pH  compris entre 7,3 et 9,3, HCO3- ] prédomine ; CO2(aq) et CO32- sont négligeables. 4.d Montrer que s2 = Ks (H3O+] / KA2. KA2 = [CO32-aq] [ H3O+aq ] / [HCO3- ] Ks = [Ca2+aq][HCO3- ] =  [Ca2+aq] KA2 [HCO3- ] / [ H3O+aq ]= s2KA2 / [ H3O+aq ]. s2 = Ks [H3O+] / KA2. 4.e Montrer que ps = -log (s) est une droite dont on donnera l'équation. log(s2) =log (Ks) + log[H3O+] -log(KA2). 2 log (s) = log (Ks) + log[H3O+] -log(KA2). -2 log(s) =  -log (Ks) - log[H3O+] +log(KA2). 2ps =pKs +pH -pKa2. ps = ½pKs -½pKa2 +½pH. ps =½(8,3 -10,3) +0,5 pH. ps = 0,5 pH -1.   5. 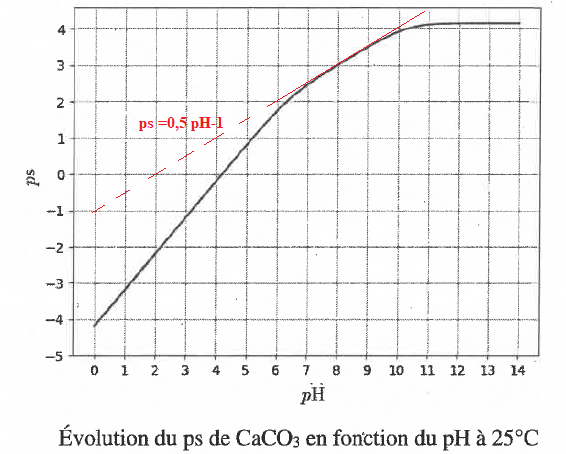5.a Vérifier la cohérence du résultat précédent avec ce graphique. 5.b Pour un pH passant de 8,1 à 7,8, calculer à partir du graphique la quantité supplémentaire de calcaire dissout par litre d'eau. Expliquer le problème des coraux. ps passe de 3,1 à 2,8 ; ps diminue de 0,3 ; s augmente de 10-0,3 =0,5 mol / L. M(CaCO3) =100 g /mol; 00,5 *100 = 50 g de calcaire dissout par litre d'eau. En injectant du dioxyde de carbone dans l'eau, le pH de celle-ci diminue et en conséquence la concentration en ion CO32- diminue. Or le squelette des coraux est du carbonate de calcium CaCO3(s). L'équilibre suivant est en conséquence déplacé vers la gauche, dissolution de CaCO3(s). Ca2+aq + CO32-aq =CaCO3(s) ... .... Exercice 2. Autour de l'eau oxygénée H2O2. 1. a. Donner la composition précise ( nombre et type de nucléons, nombre d'électrons) des atomes d'oxygène et d'hydrogène. Atome d'oxygène : 8 protons ; 8 électrons et 16-8 = 8 neutrons. Atome d'hydrogène : 1 proton ; 1 électtron. 1.b. Ecrire les configurations électroniques de ces deux atomes dans leurs états fondamentaux. Identifier les électrons de valence. H : 1 s1. Un électron de valence. O : 1 s2 2s2 2p4. 6 électrons de valence. 1.c. Donner les schémas de Lewis du dioxygène, de l'eau et de l'eau oxygénée. 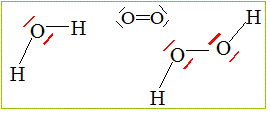1.d. Déterminer les nombres d'oxydation de l'oxygène et de l'hydrogène dans l'eau et dans l'eau oxygénée. En déduire l'existence des couples oxydant / réducteur. Le nombre d'oxydation de l'hydrogène est égal à 1. Dans l'eau le nombre d'oxydation de l'oxygène est -II. Dans l'eau oxygénée le nombre d'oxydation de l'oxygène est -I. E°(O2 (g) / H2O2 aq) = 0,68 V ; E°(H2O2 aq / H2O l) = 1,77 V. 1.e Ecrire les deux demi-équation d'oxydo-réduction des couples où interveint l'eau oxygénéne. O2 /H2O2 : E° = 0,69 V. H2O2 = O2 +2H++2e- (1) : H2O2 joue le rôle de réducteur qui s'oxyde. H2O2 /H2O : E° =1,77 V. H2O2 +2H++2e- = 2H2O (2) : H2O2 joue le rôle d'oxydant qui se réduit. 1.f En déduire que 2H2O2 aq = 2H2O(l) + O2 (g). (1) +(2) donne : 2H2O2 aq = 2H2O(l) + O2 (g). 1.g. Prévoir qualitativement si cette réaction sera favorisée dans le sens direct ou indirect. La réaction de décomposition de l'eau oxygénée à l'abri de la lumière ( flacon opaque) et à température peu élevée est très lente. 2. Etude cinétique de la décomposition de H2O2. La loi de vitesse est d'ordre 1 par rapport à l'eau oxygénée. On note C(t) la concentration de l'eau oxygénée à la date t. Concentration initiale de l'eau oxygénée C0 = 1,00 103 mol m-3. 2.a Exprimer la vitesse de disparition de l'eau oxygénée en fonction de k et C(t). En déduire par analyse dimensionnelle l'unité de k. 2.b . Déterminer l'équation différentielle à laquelle obéit C(t). v = -dC(t) / dt = k C(t). dC(t) /dt +k C(t) = 0 ; k s'exprime en seconde -1. 2.c. En déduire la loi horaire C(t). C(t) = Cste exp(-kt) ;  C(t=0) = C0 = Cste. C(t) = C0 exp(-kt) 2.d Définir le temps de demi-réaction t½; l'exprimer littérallement et faire l'application numérique. Le temps de demi-réaction est la durée au bout de laquelle la concentration initiale est divisée par 2. A t= t½; C(t½) = 0,5 C0 = C0 exp(-kt½). 0,5 = exp(-kt½) ; ln(0,5) = -ln(2) = -kt½ ; t½ = ln(2) / k avec k = 2,01 10-3 s-1. t½ = ln(2) / ( 2,01 10-3 ) =350 s. 2.e. On lit qu'un flacon d'eau oxygénée, jamais ouvert, est stable durant plusieurs mois. Commenter. La réaction de décomposition de l'eau oxygénée à l'abri de la lumière ( flacon opaque) et à température peu élevée est très lente. 3. Etude thermodynamique de cette décomposition. DfH°(H2O2 l)=-187 kJ / mol ; DfH°(O2 g)=0 kJ / mol ; DfH°(H2Ogl)=-285 kJ / mol. 3.a Exprimer et calculer l'enthalpie standard de la réaction de décomposition de l'eau oxygénée à 298 K. Commenter qualitativement quant à la possibilité d'utiliser l'eau oxygénée comme carburant. DrH° =DfH°(H2O(l)) +½DfH°(O2)- DfH°(H2O2(l)). DrH° =-285-(-187) = -98 kJ/mol. 98 kJ pour 34 g d'eau oxygénée soit 2,9 MJ / kg. Valeur très inférieure au pouvoir calorifique de l'essence ( ~40 MJ / kg). DrH° étant négative, la décomposition de l'eau oxygénée est exothermique. 3.b Construire le tableau d'avancement de cette réaction pour une mole d'eau oxygénée. avancement (mol) H2O2 aq   = H2O(l) +0,5 O2 (g). initial 0 1 solvant 0 final 1 0 1 3.c. On suppose que l'enthalpie de cette réaction est indépendante de la pression et de la température. Exprimer le transfert thermique molaire fourni par la décomposition de l'eau oxygénée à pression constante. Faire l'application numérique. En déduire la valeur du tranfert thermique massique correspondant. DrH° =-285-(-187) = -98 kJ/mol. 98 kJ pour 34 g d'eau oxygénée soit 2,9 MJ / kg.

menu