Tissage
d'une voile de bateau,
bac Asie 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Diamètre du fil de carbone : a= 10 µm. Espacement entre les fils : b compris entre 12 et 25 µm..
Observation directe.
On considère un observateur qui regarde la voile à la distance dm = 25 cm. Il cherche à distinguer l'épaisseur des fils
1. Exprimer le champ angulaire qa en fonction de a et dm.
qa ~a / dm.
2.3. L'évaluer. Conclure.
10-5 / 0,25=4 10-5 rad, valeur inférieure au pouvoir séparateur de l'oeil. On ne peut pas distinguer l'épaisseur des fils à l'oeil nu.
L'observateur utilise une loupe.
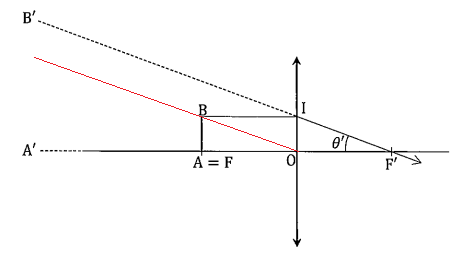
4. Montrer que q'a = a / f '.
tan q'a= AB / OF =a / f '.
Pour les petits angles : q'a ~ a / f '.
5. En déduire que l'observateur peut distinguer l'épaisseur des fils lorsque f ' < a / e.
L'observateur distigue l'épaisseur des fils si q'a est supérieur au pouvoir séparateur de l'oeil noté e.
a / f ' > e f ' < a / e.
6. On dispose de trois loupes de distance focale : 12,5 cm, 5,0 cm, 2,5 cm. Laquelle (lesquelles) choisir ?
a =10-5 m ; e =3 10-4 rad.
10-5 / (3 10-4) =0,033 m ou 3,3 cm.
f ' < 3,3 cm. Loupe de distance focale 2,5 cm.
Analyse par interférences.
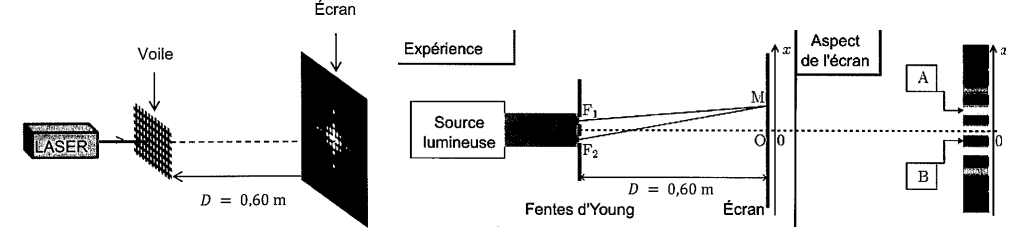
7. Indiquer en justifiant la nature des interférences aux points A et B.
Point A lumineux, interférences constructives.
Point B, noir, interférences destructives.
8. Rappeler la définition de l'interfrange.
L'interfrange est la distance séparant deux franges consécutives de même nature.

9. Rappeler la condition sur la différence de chemin optique d pour observer des interférences constructives.
La différence de chemin optique doit être égale à un multiple entier de la longueur d'onde.
10. Montrer que i = D l / b.
d = bx / D = k l avec k entier.
Pour k = 1, la plus petite valeur de x donnant la première frange brillante est i.
b i / D = l ; i = D l / b.
11. Déterminer la valeur de i.
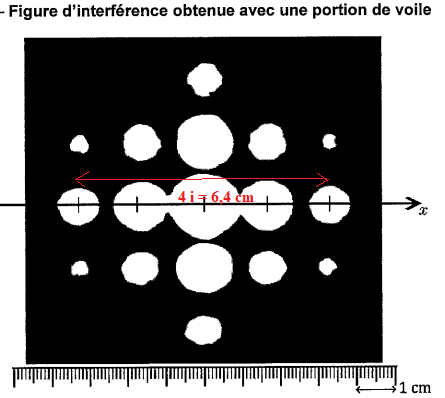
4 i = 6,4 cm ; i = 1,6 cm.
12. Estimer l'incertitude type sur i.
u(i) = 1 mm.
13. En déduire une valeur de b avec son incertitude.
b = D l / i = 0,60 x650 10-9 / 0,016 =2,4 10-5 = 24 µm.
u(b) / b = [(u(D) / D)2 +(u(i) / i)2+(u(l) / l)2]½ ;
u(b) =2,4 10-5 x[(0,01 / 0,6)2 +(0,1 /1,6)2+(10 /650)2]½ =1,6 10-6 m.
b = 2,4 ±2 µm.
14. Discuter la
compatibilité de cette mesure avec le tissage d'une zone soumise
à de faibles contraintes pour laquelle b = 25 µm..
b appartient bien à l'intervalle [22 ; 26 µ]. Les résultats sont compatibles.
|
...
|
....
|
On réalise une seconde figure d'interférences avec une autre portion de voile.
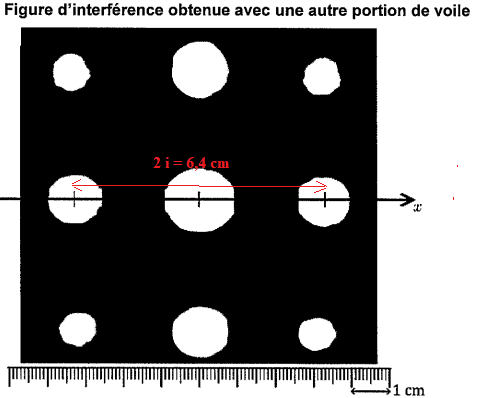
Justifier que cette portion de voile est prévue pour supporter des contraintes plus fortes.
i = 3,2 cm, valeur plus importante que dans le cas précédent.
Or b = l D / i, à lD constant, b est plus faible.
Le tissage étant plus serré, il peut supporter des contraintes plus fortes.
|
ane.
|
|
|