Vol du drone Ingenuity sur Mars, bac centres étrangers 2024

Le rover Perseverance actuellement en mission sur la planète Mars a embarqué avec lui un autre robot : Ingenuity, un petit drone destiné à voler sur Mars. Les missions d’Ingenuity sont multiples :
reconnaissance optique du terrain, étude des communications dans l’atmosphère ténue de Mars et surtout le premier test de vol motorisé sur une autre planète.
Masse du drone : m = 1,8 kg ;
Valeur de l’accélération de la pesanteur terrestre : g_Terre = 9,8 m·s^-2 ;
Valeur de l’accélération de la pesanteur sur Mars : g_Mars = 3,7 m·s^-2.
Lors de ses missions, la valeur de la vitesse maximale atteinte par Ingenuity est v₀ = 6,0 m.s^-1 et l’altitude maximale atteinte reste inférieure à 15 m.
La phase la plus délicate du vol du drone est sa fin, le choc avec le sol. La solution retenue pour éviter de détériorer le drone est d'arrêter la propulsion à un mètre au-dessus du sol et de laisser le drone atteindre le sol en chute libre. On considère, le sol de Mars étant sablonneux, que le drone s’arrête brutalement quand il touche le sol, aussi bien dans son mouvement vertical qu’horizontal.
Le train d’atterrissage a été conçu pour supporter une certaine vitesse maximale à l’arrivée sur le sol sans détruire l’engin.
Le but de l’exercice est d’étudier le mouvement du centre de masse du drone en chute libre, lors de la dernière phase du vol à partir d’un mètre au-dessus du sol et de déterminer la valeur de la vitesse atteinte lors de l’impact avec le sol, puis de comparer ce mouvement avec celui qui serait réalisé sur Terre dans les mêmes conditions.
On associe au référentiel de la planète Mars un repère d’espace schématisé sur la figure ci-après.

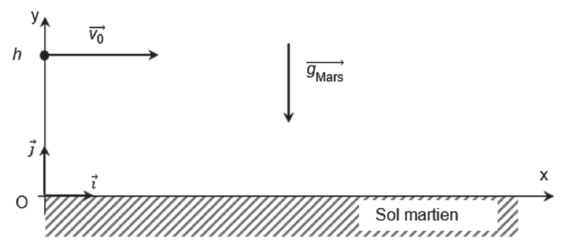
On considère que la vitesse du drone au moment de l’arrêt de la propulsion est horizontale et de valeur v₀ = 6,0 m·s^-1 ; le drone se trouve à cet instant à une altitude notée h.
Q1. Rappeler la définition du modèle de la chute libre.
Un corps en chute libre n'est soumis qu'à son poids.
Q2. Prévoir sans calcul, lors d’une chute libre sans vitesse initiale et pour une même hauteur initiale, laquelle des situations (sur Terre ou sur Mars) serait la plus contraignante du point de vue de la solidité du train d’atterrissage.
Energie mécanique du système : sur terre mg_Terre h ; sur Mars mg_Mars h ;
g_Terre > g_Mars ; l'énergie mécanique est la plus importante sur Terre et la situation d'un atterrissage sur Terre sera plus contraignante pour le train d'atterissage.
Q3. Après avoir effectué un bilan des forces appliquées au drone dans le cadre du modèle de la chute libre, donner l’expression du vecteur accélération du drone ainsi que les coordonnées de ce vecteur dans le repère.
Le drone n'étant soumis qu'à son poids, le vecteur accélération est vertical vers le bas, de norme -g_Mars.
La vitesse du drone au moment de l’arrêt de la propulsion, choisi comme origine des temps t = 0, est horizontale et de valeur v₀ = 6,0 m·s^-1; le drone se trouve à cet instant à une altitude notée h = 1,0 m.
Q4. Déduire de la question 3 les coordonnées du vecteur vitesse dans le repère au cours du temps. Qualifier le mouvement horizontal du drone avant impact et en déduire la valeur de la vitesse horizontale du drone lorsqu’il touche le sol.
La vitesse est une primitive de l'accélération :
v_x = v₀. v_y =-g_Mars t.
Le mouvement du drone selon l'horizontale est rectiligne uniforme.
La valeur de la vitesse horizontale du drone lorsqu’il touche le sol est v₀ = 6,0 m /s..
Les équations horaires du mouvement lors de la chute ont pour expression :
x(t) = v₀ × t et y(t) = -½g_Mars t² +h.
Q5. Exprimer la date t_impact à laquelle le drone touche le sol en fonction de h et g_Mars.
0 = -½g_Mars t² +h ; t = (2h /g_Mars) ^½= (2 x1,0 / 3,7)^½ =0,735 ~0,74 s.
Q6. Calculer la valeur de la position horizontale de l’impact du drone sur le sol martien x_impact.
x_impact= 6,0 x0,735 =4,4 m.
Calculer la valeur de cette position si l’expérience se faisait dans les mêmes conditions sur Terre.
t = (2h /g_Terre) ^½= (2 x1,0 / 9,8)^½ =0,45 s.
x_impact= 6,0 x0,45 =2,7 m.
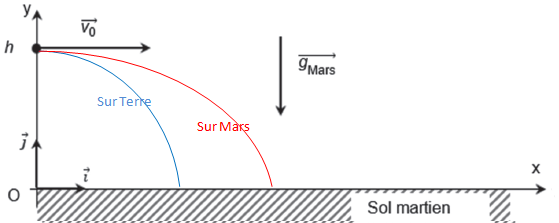
Q7. Tracer sans souci d’échelle sur un schéma identique à celui de la figure, l’allure de la trajectoire du drone entre l’instant t = 0 et l’instant où il touche le sol sur Mars. Tracer sur le même schéma l’allure de la trajectoire du même drone, dans les mêmes conditions initiales, si cette chute s’effectuait sur Terre. On distinguera clairement les deux courbes (légendes, couleurs, etc).

Q8. Vérifier que la valeur de la vitesse du drone, lorsqu’il touche le sol de la Terre, est d’environ 7,5 m·s^-1. En déduire la valeur de son énergie cinétique Ec.
v= (v₀² + v_y²)^½ = (v₀² + (g_Terre t.)²)^½ =(6² + (9,8 *0,45.)²)^½ ~7,5 m s^-1.
Ec = 0,5 x1,8 x7,5² =51 J.
Q9. Prévoir si un drone capable de résister à un choc avec cette valeur de Ec sur Terre, pourra subir sans dommage un choc dans les mêmes conditions initiales sur Mars.
Sur Mars : v= (v₀² + v_y²)^½ = (v₀² + (g_Mars t.)²)^½ =(6² + (3,7 *0,74)²)^½ ~6,6 m s^-1.
Ec = 0,5 x1,8 x6,6² =39 J.
Le choc sur Mars est moins violent que sur Terre. Le drone ne subira pas de dommage.