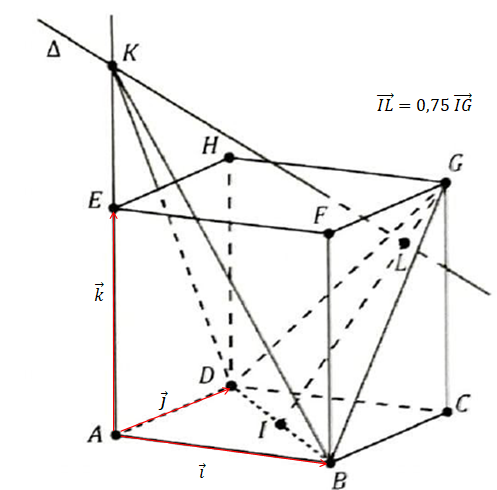
Mathématiques, Bac Métropole 09 / 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1. 6 points. On considère le cube ABCDEFGH de côté 1. I est le milieu du segment BD. 1. a Préciser les coordonnées des points D, B, I et G. D(0 ; 1 ; 0) ; B (1 ; 0 ; 0) ; I(0,5 ; 0,5 ; 0) ; G ( 1 ; 1 ; 1). 1.b. Montrer que les coordonnées du point L sont ( 7 /8 ; 7 /8 ; 3 /4). 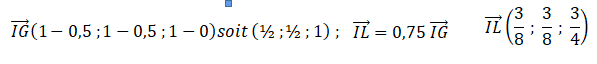xL-xI = 3 /8 ; xL=xI + 3 /8= 1/2 +3 /8 =7/8. yL-yI = 3 /8 ; yL=yI + 3 /8= 1/2 +3 /8 =7/8. zL-zI = 3 /4 ; zL=xzI + 3 /4= 0 +3 /4 =3/4. 2. Vérifier qu'une équation cartésienne du plan ( BDG) est x+y-z-1=0. B appartient à ce plan : axB+byB+c zB+d = 0 ; a+d=0 ; d = -a. D appartient à ce plan : axD+byD+c zD-a = 0 ; b-a=0 ; a = b. G appartient à ce plan : axG+ayG+c zG-a = 0 ; a+c=0 ; c = -a. ax+ay-az-a=0 soit x+y-z-1=0. 3. On considère la droite D perpendiculaire au plan (BDG) passant par L. a. Justifier qu’une représentation paramétrique de la droite D est :  x = 7 /8 + t ; y = 7/ 8 + t ; z = 3 /4 − t avec t réel. Coordonnées d'un vecteur normal au plan (BDG) = coordonnées d'un vecteur directeur de la droite (D) : (1 ; 1 ; -1) Par suite x = t+xL = t+7/8 ; y = t+yL = t+7 /8 ; z = -t +zL = -t +3/4 avec t réel.  b. Montrer que les droites D et (AE) sont sécantes au point K de coordonnées ( 0 ; 0 ; 13/ 8 ¶ . Représentation paramétrique de la droite (AE) : x =0 ; y =0 z =k+1 avec k réel. Dans l'hypothèse où les droites D et (AE) sont sécantes en K : xK=7 /8 + t =0 ;t = -7 /8 ; yK=7/ 8 + t =0 est vérifié. zK=3/4-t=3/4+7/8=13/8. L'hypothèse est valide. c. Que représente le point L pour le point K ? Justifier la réponse. 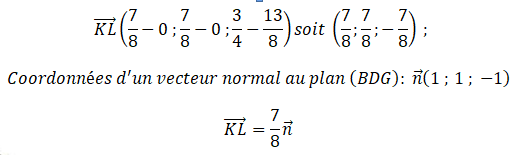L est le projeté orthogonal du point K sur le plan ( BDG). 4. a. Calculer la distance KL. KL2 =(7/8)2 +(7/8)2 +(3/4-13/8)2=(7/8)2 +(7/8)2 +(-7/8)2 = 3x(7/8)2  ; KL = 7 / 8 x3½. b. On admet que le triangle DBG est équilatéral. Montrer que son aire est égale à 3½ /2. Base GBD ; hauteur relative à cette base GI ;  BD = 2½ ; GI2= 0,52 +0,52 +12 =1,5  ; GI = (3/2)½. Aire du triangle DBG : BD xGI / 2 = 2½x(3/2)½ / 2 =3½ /2. . c. En déduire le volume du tétraèdre KDBG. Aire du triangle DBG x KL / 3 =3½ /2 x7 / (8 x3 )x3½=7 / 16. . 5. On désigne par a un réel appartenant à l’intervalle ]0 ; +∞[ et on note Ka le point de coordonnées (0 ; 0 ; a).  a. Exprimer le volume Va de la pyramide ABCDKa en fonction de a. Aire de base = aire du carré ABCD = 1. Hauteur :KA = a. Volume = aire de base x hauteur / 3 = a /3.  b. On note Da la droite de représentation paramétrique : x = t ′ ; y = t ′ ; z = −t ′ + a où t ′ est un réel. On appelle Ia le point d’intersection de la droite Da avec le plan (BDG). Montrer que les coordonnées du point La sont ( a +1)/ 3 ; (a +1)/ 3 ; (2a −1)/ 3. La appartient à la fois au plan (BDG) et à la droite Da. xIa+yIa-zIa-1=0.; t'+t'+t'-a-1=0 ; 3t'-a=1 ; t' =(1+a)/3. xIa=.(1+a) / 3 ; yIa=.(1+a) / 3 ; zIa= -(1+a) / 3 +a=(2a −1)/ 3.   c. Déterminer, s’il existe, un réel strictement positif a tel que le tétraèdre GDBKa et la pyramide ABCDKa sont de même volume. Volume Va de la pyramide ABCDKa  = a /3. Volume V du tétraèdre GDBKa  : Aire du triangle DBG x KaLa / 3 =3½ /2  xKaLa / 3= 3½  x KaLa / 6. KaLa2 =(a+1)2/9 +(a+1)2/9 +(-a-1)2/ 9=(a+1)2 / 3 ; KaLa =(a+1) / 3½. V=(a+1) / 6. Egalité des volumes : (a+1) / 6 = a /3 ; (a+1) / 2 = a ; a =1. Il existe un réel positif tel le tétraèdre GDBKa et la pyramide ABCDKa sont de même volume. Exercice 2. 5 points. Partie A.  Un artisan crée des bonbons au chocolat dont la forme rappelle le profil de la montage locale représentée. La base d’un tel bonbon est modélisée par la surface grisée, définie ci-dessous dans un repère orthonormé d’unité 2 cm. 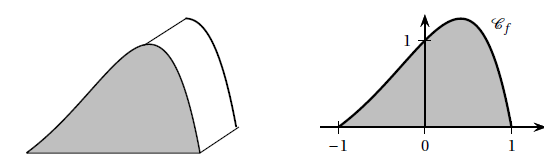Cette surface est délimitée par l’axe des abscisses et la représentation graphique notée Cf de la fonction f définie sur [−1 ; 1] par :f (x) = (1−x2)ex . L’objectif de cette partie est de calculer le volume de chocolat nécessaire à la fabrication d’un bonbon au chocolat. 1. a. Justifier que pour tout x appartenant à l’intervalle [−1 ; 1] on a f (x)>0. Le terme en exponentielle est strictement positif. (1-x2) est positi ou nul. (1−x2)ex > 0. b. Montrer à l’aide d’une intégration par parties : On pose u = 1-x2 ; v' = ex ; u' = -2x ; v = ex. 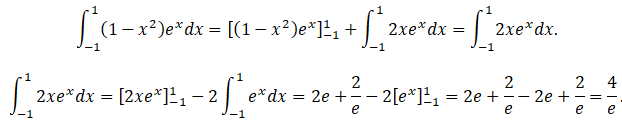2. Le volume V de chocolat, en cm3, nécessaire à la fabrication d’un bonbon est donné par : V = 3×S où S est l’aire, en cm2, de la surface colorée. En déduire que ce volume V , arrondi à 0,1 cm3 près, est égal à 4,4 cm3. V = 3 x4 /e ~4,4 cm3. Partie B. On s’intéresse maintenant au bénéfice réalisé par l’artisan sur la vente de ces bonbons au chocolat en fonction du volume hebdomadaire des ventes. Ce bénéfice peut être modélisé par la fonction B définie sur l’intervalle [0,01 ; +∞[ par : B(q)= 8q2[2−3 ln(q)]−3. Le bénéfice est exprimé en dizaines d’euros et la quantité q en centaines de bonbons. On admet que la fonction B est dérivable sur [0,01 ; +∞[. On note B′ sa fonction dérivée. 1. a. Déterminerla limite de B(q) en plus l'infini. ln(q) tend vers + oo ; -ln(q) tend vers -oo ; 2-3 ln(q) tend vers -oo. q2 tend vers +oo ; par produit des limites B(q) tend vers - oo. b. Montrer que, pour tout q >0,01, B′(q)= 8q(1−6 ln(q)). On pose u = 8q2 et v = 2-3 ln(q). u' = 16q ; v' = -3 /q. u'v+v'u = 16q(2-3ln(q)) -24q =8q-48 q ln(q)=8q(1-6 ln(q)). c. Étudier le signe de B′(q), et en déduire le sens de variation de B sur [0,01 ; +∞[. Dresser le tableau de variation complet de la fonction B. 8 q >0 ; B'(q) a le signe de 1-6 ln(q). Si q = exp(1/6), B'=0. Si q < exp(1/6), B' > 0 et B(q) est strictement croissante. Si q > exp(1/6), B' < 0 et B(q) est strictement décroissante. 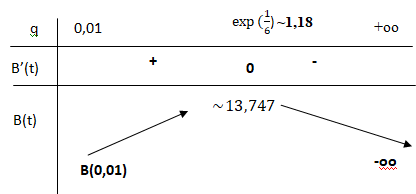d. Quel est le bénéfice maximal, à l’euro près, que peut espérer l’artisan ? 8 x(exp(1/6))2 [2-3 ln(exp(1/6)]-3 ~11,16 x1,5-3~13,747 dizaines d'euros. 2. a. Montrer que l’équation B(q) = 10 admet une unique solution ß sur l’intervalle [1,2 ; +∞[. Donner une valeur approchée de ß à 10−3 près. La fonction B est continue car dérivable et strictement décroissante sur l(intervalle [1,18 ; +oo[. De plus B(1,18) ~13,7 et B(Q) tend vers -oo si q tend vers plus l'infini. D'après le théotème de la bijection, l'équation B(q) = 10 admet une unique solution sur l’intervalle [1,2 ; +∞[. La calculatrice donne ß ~1,558. b. On admet que l’équation B(q)= 10 admet une unique solution a sur [0,01 ; 1,2[. On donne a ≈ 0,757. En déduire le nombre minimal et le nombre maximal de bonbons au chocolat à vendre pour réaliser un bénéfice supérieur à 100 euros. Le nombre de bonbons est compris entre 76 et 155. ... .... Exercice 3. 5 points. 1. On considère une suite (tn) vérifiant la relation de récurrence : pour tout entier naturel n, tn+1 =−0,8tn +18. Affirmation 1 : La suite (wn) définie pour tout entier naturel n par wn = tn −10 est géométrique. Vrai. wn+1 = tn+1 −10 =−0,8tn +18-10=−0,8tn +8= -0,8( tn-10)= -0,8 wn. 2. On considère une suite (Sn) qui vérifie pour tout entier naturel n non nul : 3n −4< Sn < 3n +4. La suite (un) est définie, pour tout entier naturel n non nul, par : un = Sn / n . Affirmation 2 : La suite (un) converge. Vrai. 3 −4 / n < un < 3 +4 / n. Quand n tend vers +oo, 4 / n tend vers zéro. D'après le théorème des gendarmes, la limite de un est égale à 3. 3. On considère la suite (vn) définie par : v1 = 2 et pour tout entier naturel n >1, vn+1 = 2−1/vn. Affirmation 3 : Pour tout entier naturel n >1, vn =(n +1) /n. Vrai. Initialisation : v2=2-1/2 =1,5 =3 /2. L'affirmation est vraie au rang 1. Hérédité : l'affirmation vn =(n +1) /n est supposée vraie. vn+1 = 2−1/vn = 2-n / (n+1)=(2n+2-n) /(n+1) =(n+2) /(n+1) =(n+1+1) / n+1). L'addirmation est vraie au rang n+1. Conclusion : l'affirmation est vraie au rang 1 et héréditaire ; elle est donc vraie pour tout entier  naturel n. . 4. On considère la suite (un) définie pour tout entier naturel n par un =en −n. Affirmation 4 : La suite (un) converge. Faux. un =en(1-n /en). Par croissance comparée, en plus l'infini, n /en tend vers zéro. La suite tend donc vers +oo. 5. On considère la suite (un) définie à l’aide du script écrit ci-dessous en langage Python, qui renvoie la valeur de un. def u(n) : valeur = 2 for k in range(n) : valeur = 0.5 * (valeur + 2/valeur) return valeur On admet que (un) est décroissante et vérifie pour tout entier naturel n : 2½ < un < 2. Affirmation 5 : La suite (un) converge vers 2½. Vrai. La suite est décroissante et minorée par 2½. D'après le théorème de la limite monotone, cette suite converge vers un réel l. Le programme Python conduit à : un+1 =0,5(un+2/un). Sur [2½ ; 2], la fonction f(x) = 0,5(x+2 /x) somme de fonctions continues sur cet intervalle est continue. l est solution de l'équation f(x) = x ; 0,5(x+2/x) = x. 1/x -0,5 x =0 ; (1-0,5x2) / x = 0. x = 2½ solution retenue ; x = -2½ n'appartient pas à [2½ ; 2]. Exercice4. 4 points. Un laboratoire fabrique unmédicament conditionné sous forme de cachets. Partie A Un contrôle de qualité, portant sur la masse des cachets, a montré que 2% des cachets ont une masse non conforme. Ces cachets sont conditionnés par boîtes de 100 choisis au hasard dans la chaîne de production. On admet que la conformité d’un cachet est indépendante de celle des autres. On note N la variable aléatoire qui à chaque boîte de 100 cachets associe le nombre de cachets non conformes dans cette boîte. 1. Justifier que la variable aléatoire N suit une loi binomiale dont on précisera les paramètres. On répète 100 fois de manière indépendante la même expérience de Bernoulli.N suit la loi Binomiale de paramètres n = 100 et p = 0,02. 2. Calculer l’espérance de N et en donner une interprétation dans le contexte de l’exercice. E = np = 2. En moyenne il y a deux cachets non conformes par boîte. 3. On arrondira les résultats à 10−3 près. a. Calculer la probabilité qu’une boîte contienne exactement trois cachets non conformes. p(N=3) =(100 3) x0,023 x(1-0,02) 97 ~0,182. b. Calculer la probabilité qu’une boîte contienne au moins 95 cachets conformes. p (N < 5) ~0,985. 4. Le directeur du laboratoire veut modifier le nombre de cachets par boîte pour pouvoir affirmer : « La probabilité qu’une boîte ne contienne que des cachets conformes est supérieure à 0,5 ». Combien de cachets une boîte doit-elle contenir au maximum pour respecter ce critère ? n : nombre de cachets par boîte.  p(X=0) > 0,5 ; (n 0) x0,020 x(1-0,02) n  > 0,5 ; 0,98n > 0,5 ; n ln(0,98) > ln(0,5) ; n < ln(0,5) / ln(0,98) ; ln(0,5) / ln(0,98)~ 34. La boîte doit contenir au maximum 34 cachets. Partie B On admet que les masses des cachets sont indépendantes les unes des autres. On prélève 100 cachets et on note Mi , pour i entier naturel compris entre 1 et 100, la variable aléatoire qui donne la masse en gramme du i -ème cachet prélevé. On considère la variable aléatoire S définie par : S =M1+M2 +. . .+M100. On admet que les variables aléatoires M1, M2, . . ., M100 suivent lamême loi de probabilité d’espérance μ = 2 et d’écart-type s. 1. Déterminer E(S) et interpréter le résultat dans le contexte de l’exercice. E(M) = E(M1) + E(M2)+...E(M100)=2 x 100 =200 ( car même espérance). 2. On note s l’écart type de la variable aléatoire S. Montrer que : s = 10s. s2 = s2(M1 )+s2(M2 )+...+s2(M100 )= 100s2. s = 10s. 3. On souhaite que la masse totale, en gramme, des comprimés contenus dans une boîte soit strictement comprise entre 199 et 201 avec une probabilité au moins égale à 0,9. a. Montrer que cette condition est équivalente à : P(|S −200|>1) < 0,1. P(199 < S < 201) > 0,9 ; P (-1 < S-200 < 1) > 0,9 ; P(|S-200| < 1) > 0,9 ; P(|S-200| > 1)< 0,1. b. En déduire la valeur maximale de s qui permet, à l’aide de l’inégalité de Bienaymé--Tchebychev, d’assurer cette condition. P(|S-E(S)| > 1) < s2/1. Dans ce cas : P(|S-200| > 1)< 10 s. La valeur maximale de s vérifie donc :10 s < 0,1 ; s < 0,01.

menu