Mathématiques,
bac STI2D et STL 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
STI2D.
Un parachutiste est en chute libre dans l’air jusqu’à l’instant t = 0
où il ouvre son parachute. Sa vitesse est alors de 50 m. s−1.
On admet par la suite que sa vitesse v, en m. s−1, en
fonction du temps t en s, est solution de l’équation différentielle sur
l’intervalle [0; +∞[ :
(E) : y′ = − 5y + 10 .
Question 1
La fonction constante g définie sur l’intervalle [0; +∞[ par g(t) = 2
est-elle une solution de l’équation différentielle (E) ? Justifier la
réponse.
g'(t) = 0 , repport dans (E) : 0 = -10+10 est vérifié.
g(t) = 2 est solution de (E).
Question 2
Montrer que les solutions de l’équation différentielle (E) sur
l’intervalle [0; +∞[ sont les fonctions f définies sur cet intervalle
par f(t)= k exp(-5t) + 2, où k est un nombre réel donné.
Solution générale de y' +5y = 0 : f(t) = k exp(-5t).
Solution générale de (E) : f(t)= k exp(-5t) +
2,
Question 3
En admettant le résultat de la question précédente, montrer que la
fonction v est donnée sur [0; +∞[ par v(t) = 48exp(-5t) + 2.
A t = 0 : 50 = k exp(0) +2 = k+2 ; k = 48.
v(t) = 48exp(-5t) + 2.
Question 4
La distance parcourue, en mètre, par le parachutiste pendant les 10
premières secondes après ouverture du parachute est donnée par
l’intégrale suivante. La calculer.
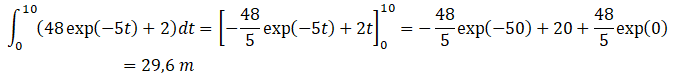 STL.
STL.
Question
1
On considère ci-dessous la courbe représentative d’une fonction f
définie sur [−2 ; 1].
Par lecture graphique, déterminer f(0).
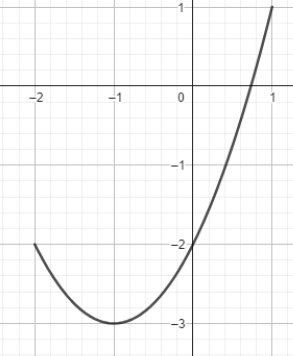
f(0) = -2.
Question 2
Soit f la fonction définie sur R par 𝑓(𝑥) = 2ex + 3x − 2.
Déterminer, en la justifiant, la limite de la fonction f lorsque x tend
vers-oo.
ex tend vers zéro ; 3 x tend vers -oo ; par somme des
limites f(x) tend vers -oo.
Question 3
Soit f la fonction définie sur R par f(x) = (3x + 2)ex−1.
En détaillant les calculs, justifier que f(1) est un entier.
f(1) = (3+2)e1-1 = 5 e0 = 5.
Question 4
Soit f la fonction définie sur ]0; +∞[ par f(x)= 2x + 1 − 1 /x.
Déterminer une primitive F de la fonction f sur ]0; +∞[.
F(x) = x2 +x -ln(x).
|
...
|
....
|
STL
Dans cet exercice, on
considère la
fonction f définie sur R par: f(x) = 5 exp(2x+1).
1. Parmi les programmes suivants,
écrits en langage Python, un seul affiche les images par f des réels 0,
0, 1; 0,2; ... ; 0,9.
Indiquer sans justifier
sur la copie la lettre correspondant à ce programme.

2. Résoudre dans R
l'équation f(x) = 5.
5 = 5 exp(2x+1) ; 1 = exp(2x+1).
ln(1) = 2x+1 ; 0 = 2x+1 ; 2x =
-1 ; x = -0,5.
3. L'affirmation
suivante est-elle vraie ou fausse ? Justifier.
«Tout nombre réel x négatif ou
nul a une image par f inférieure ou
égale à 5. »
f '(x) = 10 exp(2x+1) > 0 ;
f(x) est strictement croissante de 0 à
+oo.
De plus f(0) = 5. L'affirmation
est vraie.
4. On considère la
fonction F définie sur R par : F(x) = 2,5 exp(2x+1)
a) Montrer que la
fonction F est une primitive sur R de la fonction f.
F '(x) =2,5 *2 exp(2x+1) = 5
exp(2x+1) = f(x).
b) En déduire la
valeur exacte. puis une valeur approchée à l'entier près, de 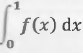
F(1) - F(0) = 2,5 exp(3) - 2,5
exp(1) =2,5(e3-e) =2,5 e(e2-1)
~43,4.
|
|
|
|