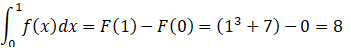Pentaoxyde
de diazote, vitesse de sédimentation d'une hématie, éthylotest,
mathématiques,
bac STL Métropole 09 / 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
Exercice
1 : (5 points)
Le pentaoxyde de diazote
Le pentaoxyde de diazote N2O5
est un puissant oxydant utilisé en synthèse organique. Il possède comme
particularité d'être un (NOx) solide à température ambiante. Sa
manipulation requiert un soin tout particulier puisqu'à température
ambiante, il peut se décomposer selon la transformation modélisée par
la réaction d'équation :
N2O5 -->2 NO2 +½ O2.
On se propose d'étudier la cinétique de cette réaction.
On introduit initialement, dans un réacteur de volume V égal à 1,0 L,
une masse m égale à 4,4 g de pentaoxyde de diazote.
1. Montrer que la
concentration en quantité de matière en N2O5 à
l'instant initial dans le réacteur est [N2O5]0 = 41 mmol L-1.
M(N2O5)=14 x 2 +5 x 16=108 g / mol.
n = m / M(N2O5)=4,4 / 108~0,041 mol = 41 mmol dans 1 L.
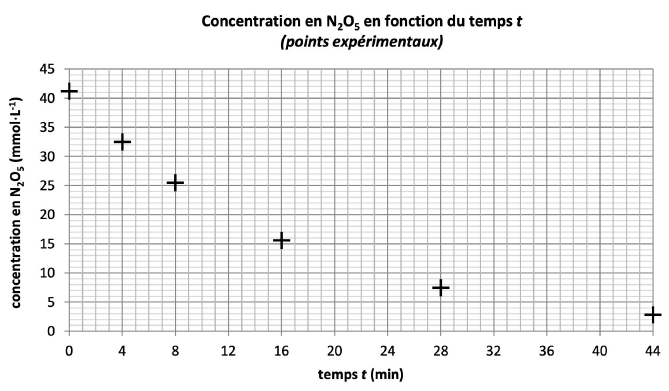
On note t le temps
écoulé à partir de l'introduction de la masse m. On effectue six mesures expérimentales de la
concentration de pentaoxyde de diazote dans le réacteur, notée [N2O5]t, pour t = 0 min, t = 4 min, t = 8 min, t
= 16 min, t = 28 min et t =
44 min. On souhaite modéliser l'évolution de la concentration de
pentaoxyde de
diazote NzOs par une
fonction f donnant la concentration de pentaoxyde de diazote dans le réacteur, exprimée en millimoles
par litre, en fonction du temps exprimé en minutes.
Pour une réaction d'ordre 0, on rappelle que la vitesse volumique de
disparition est constante au cours du temps.
2. Justifier qu'on
peut écarter l'hypothèse d'une cinétique d'ordre 0 par rapport au
réactif pentaoxyde de diazote.
Les points ne sont pas alignés.
On fait l'hypothèse que la réaction suit une cinétique d'ordre 1 par
rapport au réactif pentaoxyde de diazote, c'est-à-dire que la vitesse
volumique de disparition du réactif vérifie la loi vdisp = k
x [N2O5]t où k est la constante de vitesse.
En conséquence, on admet que la fonction f est solution de l'équation
différentielle du premier ordre suivante:
y' + k y = 0
3. Vérifier que la
fonction f définie sur l'intervalle [0; 44] par f(t) = 41 e-kt
est la solution de l'équation différentielle qui vérifie la condition
initiale f(0) = 41.
f '(t) = -41 k e-kt ; repport dans l'équation :
-41 exp(-kt) +41 exp(-kt)=0 est bien vérifié.
f(0) = 41 exp(0) = 41.
4. Montrer que
In(f(t)) = -kt + In( 41).
ln(f(t)) = ln(41) + ln(exp(-kt)) = ln(41) -kt.
On a représenté le logarithme népérien de la concentration de
pentaoxyde de diazote obtenue dans l'expérience pour t = 0 min, t = 4
min, t = 8 min, t = 16 min, t = 28 min et t = 44 min. La droite tracée
approxime les points.
5. Justifier que
l'hypothèse d'une cinétique d'ordre 1 par rapport au réactif pentaoxyde
de diazote est compatible avec les données expérimentales.
6. Déterminer le
coefficient directeur de la droite tracée.
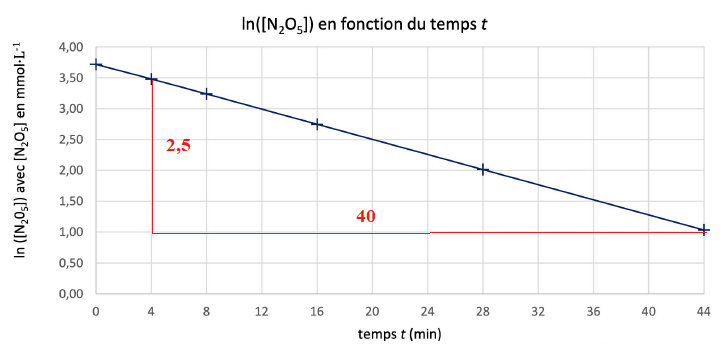
La droite passe par les points expérimentaux : la cinétique d'ordre 1
est donc valide.
Coefficient directeur de cette droite : -2,5 / 40 ~ -0,063 min-1.
7. En déduire que
la valeur de la constante de vitesse k est environ égale à 0,063 min-1.
-k = -0,063 ; k =0,063 min-1.
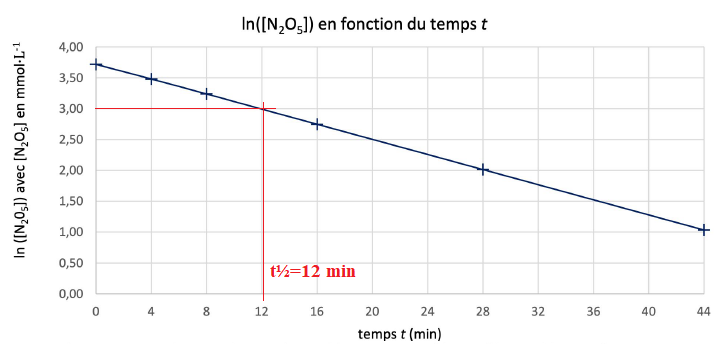
8. Calculer la valeur de ln ([N2O5]0 /2) puis résoudre graphiquement l'équation
f(t) = 20,5 .
ln ([N2O5]0 /2) = ln(20,5) =3,02.
 9. Grâce à l'expression f(t) =[N2O5]t = [N2O5]0 x e-kt, montrer que le temps
de demi-réaction t½ s'exprime par la relation:
9. Grâce à l'expression f(t) =[N2O5]t = [N2O5]0 x e-kt, montrer que le temps
de demi-réaction t½ s'exprime par la relation:
t ½ = ln(2) / k.
[N2O5]t½ =½ [N2O5]0 =[N2O5]0
exp(-kt½).
0,5 =exp(-kt½) ; ln
(0,5) = - ln(2) = -kt½ ; t ½ = ln(2) / k.
10. Calculer la valeur numérique du
temps de demi-réaction t½.
t ½ = ln(2) / 0,063~ 11 min..
11. Comparer les résultats des
questions 8 et 10.
A 10 % près les deux résultats sont en accord.
Exercice 2 :(6
points)
Vitesse de sédimentation
d'une hématie
La détermination de la vitesse de sédimentation d'une hématie (globule
rouge) est un test couramment réalisé au laboratoire d'analyses
biologiques pour surveiller l'état inflammatoire d'un patient.
Une des méthodes utilisées est la méthode de Westergreen. Elle
consiste, dans un premier temps, en la réalisation d'un mélange
constitué de sang issu du prélèvement réalisé sur le patient avec un
anticoagulant puis, dans un second temps, en son introduction dans un
long tube vertical gradué. Le biologiste dépose alors le tube
verticalement sur son support et laisse « décanter» le mélange. En
effet, les hématies sédimentent, c'est-à-dire qu'elles descendent au
fond du tube tandis que le haut du tube est constitué du plasma
sanguin. Au bout d'une durée t
le biologiste mesure la hauteur de la colonne de plasma sanguin
dépourvue d'hématies.
L'objectif de cet exercice est de déterminer un ordre de grandeur de la
« durée caractéristique» nécessaire à ce protocole.
On modélise la chute d'une hématie dans le plasma sanguin par le
mouvement rectiligne d'un point matériel noté G selon un axe (0, k)
vertical dirigé vers le bas, avec k un vecteur unitaire. La norme de la
vitesse instantanée v(t) est donc égale à
celle de la coordonnée du vecteur vitesse selon l'axe (0, k) à
l'instant t. Le point matériel G est notamment soumis à une force de
frottement fluide, notée f, et à la poussée d'Archimède PA
due au plasma sanguin. L'étude est menée jusqu'à la
question 8 dans le référentiel terrestre supposé galiléen.
Données:
- masse volumique d'une hématie: μH = 1300 kg· m-3 ;
- masse volumique du plasma sanguin: μp = 1060 kg· m-3
;
- rayon d'une hématie assimilée à une sphère: r = 2,0 x 10-6
m ;
- intensité de la pesanteur terrestre: g = 9,8 m . s-2;
coefficient de frottement: k = 4,9 X 10-8 kg. s-1.
Relations:
- volume d'une sphère: V = 4/3 pr3
;
- expression de la force de frottement fluide qui s'exerce sur une
hématie: f = -k x v avec v la vitesse instantanée de chute de l'hématie;
- expression de la poussée d'Archimède PA qui agit sur
une hématie:
FA = 4/3 pr3 μp x g
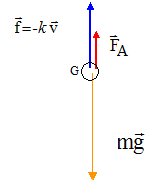
1. Préciser la troisième
force qui, en plus de f et PA s'exerce sur le point matériel
G et est à l'origine de sa chute..
Le poids de l'hématie.
2. Appliquer la
seconde loi de Newton au point matériel G de masse m afin de déterminer
la relation entre son accélération ai et les trois vecteurs forces
s'appliquant sur lui.
Selon un axe vertical orienté vers le bas : ma = mg-kv -FA.
Dans la suite de l'exercice, on considère le régime permanent établi:
la norme de la vitesse instantanée v(t) du point matériel G est
supposée avoir atteint une valeur Vlirn constante appelée
vitesse limite.
3. Simplifier la
relation écrite à la question 2 sans chercher à expliciter les trois
vecteurs forces.
A vitesse constante, l'accélération est nulle.
mg-kv -FA =0.
4. Donner les coordonnées de chaque
force selon l'axe (0, k) vertical dirigé vers le bas.
P = mg ; f = k vlim ; FA = 4/3 pr3 μp x g
5. Sans souci d'échelle,
représenter, sur un schéma clairement légendé, les trois forces
modélisant les actions mécaniques s'exerçant sur une hématie modélisée
par un point matériel noté G.
Un calcul non demandé permet de déduire l'expression de la vitesse
limite Vlirn de ce qui précède:
vlim = 4 p
r3 g(µH-µP) / (3k).
6. Calculer la
valeur de la vitesse limite en exprimant le résultat avec deux chiffres
significatifs et dans l'unité du système international. L'application
numérique devra être posée.
vlim = 4 x3,14 x(2,0 10-6)3 x9,8
(1300-1060) / (3 x4,9 10-8) =1,6 10-6 m s-1.
On prend pour la suite la valeur approchée Vlirn = 2 10-6 m s-1.
7. Déterminer la distance parcourue
par une hématie ayant atteint cette vitesse limite pour une durée de 1
h.
2 10-6 x 3600=7,2 10-3 m =7,2 mm.
On considère qu'une distance parcourue par les hématies de l'ordre de 5
mm en fin de sédimentation permet une mesure avec une incertitude
minimale.
8. Conclure quant à
la pertinence d'une durée d'examen d'une heure.
7,2 mm est du même ordre de grandeur que 5 mm : la durée d'une heure
est donc pertinente.
Pour diminuer la durée d'examen, il est possible d'utiliser une «
ultracentrifugation ».
Dans ce cas, l'expression de la norme de la vitesse limite devient dans
le référentiel d'étude:
vlim = 4 p r3 a(µH-µP)
/ (3k).
où a représente la norme de l'accélération à laquelle est soumis
l'échantillon placé dans la centrifugeuse. On précise qu'une
centrifugeuse est un appareil avec lequel le technicien peut soumettre
l'échantillon à de grandes valeurs d'accélération.
9. Expliquer
l'intérêt d'une accélération de norme la plus grande possible.
La vitesse limite est plus importante et la durée de l'examen plus
faible.
|
...
|
....
|
Exercice 3 : Mathématiques (4 points)
Question 1
Soit t la fonction définie sur R part f(x) = 3exp(5x) + 1.
Calculer f(0) en détaillant les calculs.
f(0) = 3 exp(0) +1 = 3+1 = 4.
Question 2
Résoudre sur l'intervalle] - ½ ; +oo[ l'équation In(2x + 1) = 7.
2x+1 = exp(7) ; 2x = exp(7) -1 ; x = ½(exp(7)-1).
Question 3
Soit g la fonction définie sur R par g(x) = 9x2+ 10x.
Déterminer une primitive G de g sur R.
G(x) = 3x3 +5x2 + constante.
Question 4:
Soit f la fonction définie sur R par f(x) = 3x2+7.
On note F la fonction primitive de ft définie sur R par F(x) = x3
+ 7x.
Déterminer 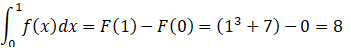
Exercice 4 ( 5 points).
Les éthylotests sont des détecteurs d'éthanol qui mettent en oeuvre des
réactions d'oxydoréduction. Cet exercice a pour but de comprendre leur
fonctionnement. L'alcool contenu dans les boissons est l'éthanol, de
formule semi-développée CH3CH2OH. L'éthanol est
absorbé, passe dans le tube digestif puis dans le sang. La
concentration en masse d'éthanol dans le sang est appelée alcoolémie.
Sa valeur maximale est atteinte une demi-heure après l'ingestion, si
l'on est à jeun, ou en une heure, si l'on a mangé.
L'estimation de cette alcoolémie est faite à partir d'une mesure
réalisée sur un volume d'air expiré. On admet que l'alcoolémie est
proportionnelle à la concentration en masse de l'éthanol dans l'air
expiré: 0,25 mg d'éthanol par litre d'air expiré correspond à une
alcoolémie de 0,50 g . L -1.
Données:
• Couples oxydant/réducteur:
- Ion dichromate (jaune) / ion chrome (III) (vert) : Cr2O72-
(aq/ Cr3+ (aq).
- Acide éthanoïque (incolore) / éthanol (incolore) : CH3COOH(aq)
/CH3CH2OH(aq).
L'équation de demi-réaction associée s'écrit :
CH3CH2OH(aq)+ H2O(l)
= CH3COOH(aq) + 4 H+ (aq) + 4 e-
- Ion permanganate (violet) / ion manganèse (incolore) : Mn04-
(aq) / Mn2+ (aq).
• Masse molaire de l'éthanol: M1 = 46,0 g. mol-1.
• Masse molaire du dichromate de potassium: M2 = 294 g. mol-1..
Le premier appareil permettant d'estimer la quantité d'alcool dans
l'air expiré, de façon suffisamment fiable et hors laboratoire, est mis
au point par Rolla N. Harger de l'Université de l'Indiana en 1931. La
personne souffle dans un ballon. L'air contenu dans ce dernier traverse
ensuite une solution de permanganate de potassium(K+, Mn04-)
acidifiée par de l'acide sulfurique. En cas de test positif, les ions
permanganate sont totalement consommés. L'équation modélisant la
transformation chimique mise en jeu lors de ce test est:
4 Mn04-
(aq) + 12 H+ (aq) +
5 CH3CH2OH(aq) ~ 4 Mn2+ (aq) + 11 H2O(l)
+ 5 CH3COOH(aq)
1. À l'aide de
l'équation écrite ci-dessus, expliquer en quoi il est pertinent
d'utiliser une solution de permanganate de potassium acidifiée par de
l'acide sulfurique.
La solution de permanganate de potassium contient la seule espèce
colorée, l'oxydant Mn04-
(aq)
2. Préciser le changement de teinte
observé lorsque le test réalisé est positif.
Passage du violet à l'incolore.
3. Déterminer le
nombre d'oxydation de l'élément manganèse dans l'ion manganèse, puis
dans l'ion permanganate.
Dans Mn2+ le nombre d'oxydation de l'élément manganèse est
+II.
Dans Mn04-
le nombre d'oxydation de l'élément manganèse est x+4x(-2) = -1 ; x =7
(+VII).
4. En déduire si, pour l'élément
manganèse, on a affaire à une oxydation ou une réduction au cours d'un
test positif.
Réduction de l'oxydant Mn04- (
diminution du nombre d'oxydation de l'élément manganèse).
De nos jours, on peut acheter des alcootests jetables dans les
stations-services, en pharmacie, ou encore en grande surface. Ils sont
constitués d'un sachet gonflable de capacité 1 L et d'un tube de verre
contenant des cristaux jaunes de dichromate de potassium en milieu
acide. Ceux-ci se colorent en vert au contact de l'éthanol.
L'automobiliste souffle dans le ballon et l'air expiré passe à travers
le tube. Si la coloration verte dépasse le trait témoin sur le tube, le
seuil toléré de 0,50 g. L -1 est dépassé.
5. Expliquer le
changement de coloration des cristaux présents dans le tube de verre au
contact de l'éthanol.
Réduction de l'ion dichromate jaune en ion chrome Cr3+ vert.
La transformation chimique se déroulant dans l'alcootest est modélisée
par la réaction
d'équation:
2 Cr2O72- (aq) + 3 CH3CH2OH(aq)
+ 16 H+ (aq) --> 4 Cr3+ (aq) + 3 CH3COOH(aq)
+ 11 H2O(l)
6. Écrire la
demi-équation électronique pour le couple Cr2O72-
(aq)/ Cr3+ (aq)
intervenant dans cette transformation chimique.
Cr2O72-
(aq)+14H+
(aq)+6e- --> 2Cr3+ (aq)+ 7 H2O(l)
7. Déterminer la quantité de
matière d'éthanol n1 expiré par litre d'air dans l'hypothèse d'une
alcoolémie égale au seuil limite de 0,50 g . L -1.
M(éthanol) = 12 x2+6+16=46 g/mol.
0,25 mg d'éthanol par litre
d'air expiré correspond à une alcoolémie de 0,50 g . L -1.
n1 = 0,25 10-3
/46=5,4 10-6 mol.
8. Montrer que la
quantité de matière d'ions dichromate qui doit alors réagir avec
l'éthanol expiré vaut n2 = 3,6 x 10-6 mol.
n2 = 2 n1 /3=5,4 10-6 x2 / 3 =3,6 10-6 mol.
9. En déduire la
masse de dichromate de potassium minimale.
M(K2Cr2O7)=294 g / mol ; 294 x 3,6 10-6
=1,06 10-3 g~1,1 mg.
|
|
|
|