Mathématiques,
bts opticien lunetier 2024
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
. |
..
..
......
...
|
EXERCICE 1 10
points
Pour
fabriquer des montures, on chauffe un matériau à 150 °C puis on le sort
du four et on le laisse refroidir à température ambiante (28 °C).
Partie A - Étude d’une série statistique
Pour étudier le refroidissement du matériau, on a réalisé des relevés de température et réalisé un croquis.
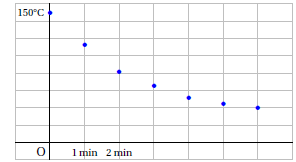
1. Expliquer pourquoi un ajustement affine de y en t n’est pas pertinent.
Les points ne sont pas alignés.
2. On pose z =ln(y −28).
Recopier et compléter le tableau. Les valeurs de z seront arrondies au centième.
t(min)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
température y °C
|
150
|
113
|
82
|
65
|
52
|
44
|
40
|
z = ln(y-28)
|
4,80
|
4,44
|
3,99
|
3,61
|
3,18
|
2,77
|
2,48
|
3. On note r le coefficient de corrélation de la série (t ; z).
On sait que r ≈ −0,999.
Sur la base de cette information, répondre aux deux questions suivantes en justifiant.
a. La corrélation de la série (t ; z) est-elle bonne?
r étant proche de -1, les deux variables sont corrélées négativement.
b. Le nuage de points (t ; z) a-t-il une allure croissante?
Non, l'allure est décroissante.
4. À l’aide de la
calculatrice, donner l’équation de la droite de régression linéaire de
z en t , selon la méthode des moindres carrés, sous la forme z = at +b.
Les coefficients a et b seront arrondis à 10−1.
z = -0,4 t +4,8.
5. En déduire une expression de y en fonction de t sous la forme
y =C exp(−0,4t) +28, où C est une constante que l’on arrondira à l’unité.
-0,4 t +4,8 = ln(y-28) ; exp(-0,4t+4,8) = y-28.
y = 28 +exp-0,4t) * exp(4,8) = 122 exp(-0,4t) +28.
Partie B - Équation différentielle.
On considère l’équation différentielle :
(E) : 5y′ +2y = 56,
où y est une fonction inconnue de la variable t , définie et dérivable sur l’intervalle [0 ; +∞[,
et où y′ est sa fonction dérivée.
1. Déterminer les solutions de l’équation différentielle
(E0) : 5y′ +2y =0.
y = B exp(-0,2t ) avec B une constante réelle.
2. Soit A un nombre réel. On considère la fonction constante g, définie par g(t ) = A.
Déterminer A pour que la fonction g soit solution de l’équation différentielle (E).
g '(t) = 0 ; repport dans (E) :2 A = 56 ; A = 28.
3. En déduire les solutions de l’équation différentielle (E).
y = B exp(-0,2t) +28.
4. Déterminer la fonction f , solution de l’équation différentielle (E), qui vérifie la condition initiale f (0) =150.
150 = B +28 ; B = 122.
Partie C - Étude de fonction
On considère la fonction f , définie sur l’intervalle [0 ; +∞[ par :
f (t )= 122exp(−0,4t) +28.
On admet que la fonction f modélise l’évolution de la température du
matériau au fil du temps : ainsi, f (t ) représente la température, en
degrés Celsius, t minutes après la sortie du four.
1. Donner la limite de f en +∞. Ce résultat est-il cohérent avec le contexte de l’exercice ?
En plu l'infini le terme en exponentielle tend vers zéro et f(t) tend vers 28°C, température ambiante.
2. On cherche à partir de quel instant la température du matériau devient inférieure à 50 °C.
a. Montrer que cela revient à résoudre l’inéquation : exp(−0,4t) < 11/61.
122exp(−0,4t) +28< 50 ; exp(-0,4t) < (50-28) / 122 ; exp(-0,4t) < 22 / 122 ; exp(−0,4t) < 11/61.
b.
Résoudre cette inéquation, puis déterminer à partir de quel instant,
exprimé en minutes et secondes, la température devient inférieure à 50
°C.
-0,4 t < ln(11 / 61) ; t < 4,28 soit t < 4 min 17 s.
3. On considère la fonction F définie sur l’intervalle [0 ; +∞[ par
F(t ) =−305exp(−0,4t) +28t .
Vérifier que la fonction F est une primitive de la fonction f sur l’intervalle [0 ; +∞[.
Calcul de la dérivée F '(t) =305 x0,4 exp(-0,4t) +28 =122 exp(-0,4t) +28 = f(t).
4. Déterminer la du matériau durant les 6 premières minutes qui suivent la sortie du four. Arrondir au dixième.
[F(6) - F(0) ) / 6 =[-305 exp(-2,4)+28 x6 +305] / 6 =74,2°C.
|
...
|
....
|
EXERCICE 2 10
points
.
Partie A. Probabilités conditionnelles.
70 % des paires de lunettes sont des modèles CLASSIQUE.
3 % des paires de lunettes sont des modèles SPORT équipées d’un autre type de verre.
21% des paires de lunettes sont équipées de verres photochromiques.
On prélève au hasard une paire de lunettes. On considère les évènements suivants :
C : « la paire de lunettes est un modèle CLASSIQUE »,
S : « la paire de lunettes est un modèle SPORT »,
L : « la paire de lunettes est équipée de verres polarisés »,
H : « la paire de lunettes est équipée de verres photochromiques »,
A : « la paire de lunettes est équipée d’un autre type de verre ».
Les résultats seront arrondis, le cas échéant, au millième.
|
Verres polarisés L
|
Verres photochromiques H
|
Autre type de verre A
|
Total
|
Modèle classique C
|
17,5 %
|
10,5 %
|
42 %
|
70 %
|
Modèle sport S
|
16,5 %
|
10,5 %
|
3 %
|
30%
|
Total
|
34 %
|
21 %
|
45%
|
100%
|
1. Donner la valeur de la probabilité P (L n S).
P (L n S) = 0,3 x0,165=0,0495~0,049.
2. Déterminer la probabilité P (L u S).
P(L u S) = P(L) + P(S) - P(L n S) =0,34 +0,30-0,0495=0,059.
3. Déterminer valeur de la probabilité de L sachant S, notée PS (L).
P(S n L) / P(S) = 0,0495 / 0,30 =0,165.
4. Les évènements L et S sont-ils indépendants? Justifier.
P(L) x P(S) =0,34 x 0,30 = 0,102 diffère de P(L n S).
L et S ne sont pas indépendants.
5. Recopier et compléter l’arbre suivant qui représente la situation décrite par le tableau.

Partie B - Loi binomiale
Parmi les clients de l’opticien, la proportion de retraités est égale à 62%.
Un jour donné, l’opticien accueille 90 clients. On note X la variable
aléatoire qui donne le nombre de retraités parmi les 90 clients
accueillis ce jour.
1. On admet que la variable aléatoire X suit une loi binomiale.
Donner ses paramètres ainsi que son espérance.
n =90 ; p = 0,62 ; E = np =55,8.
2. Calculer la probabilité P(X = 55). Arrondir au millième.
P(X =55) =0,085.
3. Quelle est la probabilité qu’au moins 50% des clients accueillis ce jour soient des retraités?
Arrondir au millième.
P(X < 50) =0,125.
Partie C - Loi normale
Le chiffre d’affaires d’un opticien en 2023 a été égal à 80 000 euros.
Il espère que son chiffre d’affaires en 2024 sera supérieur.
Son chiffre d’affaires, en euros, estimé pour 2024, est donné par une
variable aléatoire Z qui suit une loi normale dont la courbe de densité
est représentée ci-dessous.
1. On note μ l’espérance de la variable aléatoire Z.
Déterminer graphiquement la valeur de μ.
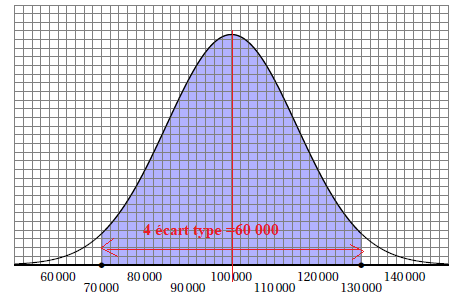
µ =100 000.
2. On note s l’écart-type de la variable aléatoire Z.
On sait que la zone grisée correspond à une probabilité égale à 0,95.
Expliquer pourquoi on a : s≈ 15 000.
4 écart type = 60 000 ; s = 15 000.
3. Quelle est la probabilité que le chiffre d’affaires en 2024 soit supérieur à celui de 2023?
Arrondir au millième.
P(Z >80 000) = 1-P(Z < 79 999) =1- 0,091=0,909.
4. Si entre 2023 et 2024, son chiffre d’affaires augmente de 30%, l’opticien embauchera un nouvel employé.
Quelle est la probabilité que l’opticien embauche un nouvel employé ?
80 000 x1,3=104 000.
P(Z >104 000) = 1-P(Z < 103 999) =0,395.
Partie D - Test d’hypothèse
Afin de développer le commerce, une commune rurale décide de construire
des parkings pour les commerçants dont la proportion de clients venant
en voiture est comprise entre 50% et 60%. Lorsque la proportion est
inférieure, le parking n’est pas nécessaire. Lorsque la
proportion est supérieure, le commerçant devra obligatoirement s’installer en périphérie de la commune.
Un opticien affirme à la mairie de cette commune que 55% de ses clients viennent en voiture.
Afin de contrôler cette affirmation, la mairie met en place un test
bilatéral au seuil de 5% sur un échantillon aléatoire de 130 clients.
On note F la variable aléatoire qui, à chaque échantillon aléatoire de 130 clients, associe la
proportion de ceux qui viennent en voiture. On suppose que F suit une loi normale d’espérance p inconnue et d’écart-type
s =[p(1−p) / 130]½..
L’hypothèse nulle est H0 : « p = 0,55 ».
L’hypothèse alternative est H1 : « p diffère de 0,55 ».
1. Justifier que, sous l’hypothèse nulle, la variable aléatoire F suit une loi normale d’espérance 0,55 et d’écart-type 0,044.
p=0,55 ; s = [0,55 x 0,45 / 130]½ =0,044.
2. Déterminer, sous l’hypothèse nulle, le réel positif h tel que
P(0,55−h < F < 0,55+h) = 0,95.
h = 1,96 x0,044=0,086.
3. Sur un échantillon de 130 clients, la mairie a noté que 88 étaient venus en voiture.
Que peut-on conclure?
Intervalle de confiance :[0,55 -0,086 ; 0,55 +0,086] soit : [0,464 ; 0,636].
88 / 130 = 0,677.
Cette valeur n'appartient pas à l'intervalle de confiance : l'opticien devra s'intaller à la périphérie.
.
|
|
|
|
|