Corrigé
physique,
Concours avenir 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
On compare la résistance thermique d’un
pilier
parallélépipédique en bois et d’un pilier en béton de même épaisseur
e=18 cm et dont la surface d’échange est S=2,5 m2.
On considère que le flux thermique à travers le pilier est égal au flux
thermique à la surface du pilier en contact avec l’air.
1. La résistance
thermique du pilier en béton vaut : l(béton) = 1,8 W m-1
K-1.
R = e /(lS) =0,18
/ (1,8 x 2,5) = 1 /25=0,04 K W-1= 40 mK W-1.
Réponse D.
2. La température de la paroi extérieure du pilier en béton est à -1°C
et celle de la paroi intérieure à 19°C, le flux thermique F au travers du pilier en
béton est alors :
F = DT / R =(19-(-1)) / 0,04 =
500 W. Réponse C.
.
3. Le coefficient d’échange
(appelé également coefficient de Newton) h avec l’air extérieur à - 6°C
(température loin de la paroi) dans ce cas vaut :
F = h S (T-Tf) ;
h=F
/(S (T-Tf) )=500/ (2,5 x(-6+1))=100 / 2,5=40 Wm-2K-1.
Réponse A.
4. Si le pilier
avait été en bois, à épaisseur et surface d’échanges égales, la perte
thermique aurait été environ :
l(bois)
= 0,15 W m-1 K-1~ 0,083 l(béton).
R(bois ) =12 R(béton).
Flux(bois) = Flux(béton) / 12= 500 /12 ~42 W.
(500-42) /500 ~0,9. 90 % plus faible. Réponse
D.
5.
Un des déchets radioactifs principaux de la fission de l’uranium est le
strontium 90 dont la demi-vie est de 29 jours. Pour un échantillon
contenant initialement N0=1030 noyaux de
strontium, au bout de 87 jours il restera :
87 = 3 x 29.
Au bout de trois demi-vie radioactive, N = N0 / 23
=1030/ 8 =1,25 1029 noyaux. Réponse
D.
6.
La loi de décroissance radioactive
décrivant l’évolution du nombre de noyaux au cours du temps en fonction
de la constante radioactive l
est :
N(t) = N0 exp(-l t).
Réponse A.
7. Pour que
l’échantillon soit inoffensif, on considère que le pourcentage de
noyaux désintégrés doit être de 99%. Pour l’échantillon de strontium
cela correspond à :
N(t) = 0,01 N0 =N0 exp(-l t) ; 0,01 = exp(-l t).
l t =ln(100) ;
l =
ln(2) / T½ =ln(2) / 29 jour-1.
t =ln(100) x29 / ln(2) ~193 jours. Réponse
C.
8) On considère
l’élévation de température, sans changement d’état, d’une masse m=100
kg de fluide caloporteur incompressible de capacité thermique massique
C=4 kJ kg-1 K-1 de la température T1 =
10°C à la température T2 =20°C. Son énergie interne a
augmenté de :
m C(T2-T1) =100 x 4 x10 =4000 kJ= 4 MJ. Réponse A.
9) Le fluide
caloporteur va ensuite parcourir des tuyaux et des radiateurs qui
réchaufferont l’air en contact avec eux, permettant ensuite le
chauffage des bâtiments grâce à des courants de convection. Réponse D.
Panneaux photovoltaïques. Lorsque la cellule est en silicium, l’énergie
minimale du photon pour pouvoir arracher un électron, appelée travail
d’extraction, vaut 4,8 eV = 4,8 x1,6 10-19 J.
10) La fréquence
minimale de l’onde pour arracher des électrons à une cellule en
silicium vaut environ :
E = h n ; n = 4,8 x1,6 10-19 /(6,63 10-34)
~1,2 1015 Hz. Réponse B.
11. La longueur
d’onde du photon doit donc être :
l <
c / n =3 108
/(1,2 1015) ~2,6 10-7 m ou 0,26 µm ou inférieure
à 260 nm. Réponse B
12. Pour un rayonnement ultraviolet de longueur d’onde l=0,1 µm=10-7 m,
l’énergie cinétique des électrons arrachés au silicium vaut :
Energie d'un photon : h c / l =6,63 10-34 x3
108 / 10-7~2 10-18 J.
Energie d'un photon - énergie d'extraction =2 10-18-4,8 x1,6 10-19 =1,2 10-18
J ou 1,2 10-18 / (1,6 10-19)=7,7
eV. Réponse D.
Les cellules placées sur les toits des bâtiments du village olympique
recevront un éclairement d’environ 1000 W/m2. Les panneaux
au silicium utilisés, de surface S=1,5 m2 chacun,
possèderont un rendement de 20%.
On considère l’éclairement constant tout au long de la journée.
13) Pour 10h
d’ensoleillement moyen par jour, on pourra donc espérer obtenir une
énergie électrique par panneau de :
Puissance électrique = 1000 x1,5 x0,20 =300 W.
Energie électrique = puissance ( W) x durée (h) =300 x 10 =3000 Wh = 3
kWh. Réponse A.
Un circuit électrique peut alors être assimilé à un circuit en série
comportant un générateur de courant continu de tension E=24 V , un
condensateur de capacité C = 10 000 µF=0,01 F et une résistance R1
= 1,5 kW.
14) La constante de
temps t de ce
circuit vaut :
R1C = 1500 x0,01 =15 s. Réponse
C.
15) La loi des
mailles appliquée à ce circuit est :
E = uR1 +uC. Réponse
D.
16) Sachant que le
condensateur était initialement déchargé, l’intensité du courant i(t)
vérifie alors l’équation :
E = R1 i(t) +uC(t) avec i(t) =q(t) /dt = CduC/dt.
E = R1CduC/dt +uC(t).
Solution générale de R1CduC/dt +uC(t) = 0 : uC(t)
= A exp(-t /(R1C))=A exp(-t /t) avec A une constante.
Solution particulière de l'équation différentielle : uC(t)= E ( condensateur
chargé).
Solution générale : uC(t) = A exp(-t /t)+E.
uC(t=0) = 0 = A+E ; A = -E.
uC(t) = -E exp(-t /t)+E = E(1-exp(-t /t)).
i(t) =CduC/dt
=EC / t exp(-t /t)= E / R1exp(-t /t). Réponse A.
17) Lors d’une
descente, le condensateur initialement déchargé se charge pendant 105
s. L’intensité moyenne du courant de charge sur cette durée vaut
environ :
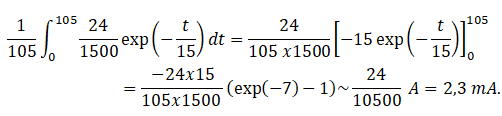 Réponse D. Réponse D.
18)
Au bout de cette durée de 105 s, le condensateur :
105 = 7 x15 ; au bout de 7 t le condensateur est
complètement chargé.
On étudie le mouvement du coureur dans un repère (xOz) dont l’axe (Ox)
est parallèle à la route, dirigé vers la droite, et l’axe (Oz)
orthogonal à la route et dirigé vers le haut.
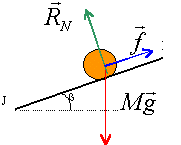
19) Les coordonnées
du poids dans le repère (xOz) sont :
Selon Oz : -Mg cos ß =-100 x10 x cos 40 ~ -0,75 Mg.
Selon Ox : -Mg sin 40 ~ -0,65 Mg. Réponse
B.
20) On peut alors
affirmer que les coordonnées des deux autres forces sont telles que :
RN = 0,75 Mg ; f = 0,65 Mg. Réponse D.
21) Sachant que la
longueur de la montée est AB= 3 km, le travail du poids lors de cette
montée vaut environ :
La composante du poids perpendiculaire au plan ne travaille pas.
W = -Mg sin 40 AB =-100 x 10 x0,65 x3000 ~ -2 106 J = -2 MJ.
Réponse C.
22) En utilisant le
théorème de l’énergie cinétique, on peut alors dire que la somme des
travaux des forces RN et f est égale à l'opoosé du
travail du poids. Réponse D.
Le coureur arrive alors dans la dernière ligne droite et déclenche le
système d’aide (on prendra cet instant pour origine des temps). Le
condensateur est initialement chargé tel que UC(t=0) = E.
Dans cette configuration, le circuit électrique peut-alors être
assimilé à un circuit en série comportant uniquement le condensateur de
capacité C = 0,01 F et le moteur, que l’on assimilera à une résistance R2
= 500 ohms..
23) La tension aux
bornes du condensateur est alors donnée par :
Uc(t) + R2i(t) = 0 avec i(t) = dq(t) /dt = C dUC(t)
/dt.
R2C dUC(t) /dt +Uc(t) =0.
Uc(t) =A exp(-t / (R2C))
avec A une constante.
Uc(t=0) = E ; A = E ; Uc(t) =E exp(-t / (R2C)).
Réponse D.
24) Le moteur n’est
en mesure de fonctionner que si la tension d’alimentation (donc la
tension aux bornes du condensateur) est supérieure à 18 V. Le coureur
va donc bénéficier de l’aide du moteur électrique pendant :
24 exp(-t / (R2C))
> 18 ; R2C= 500 x0,01=5.
exp(-t / 5) > 18 /24 ; exp(-t / 5) >0,75 ;-t / 5 >
ln(0,75) ; t < -5 ln(0,75) ; t < 1,5 s. Réponse A.
|
...
|
....
|
Epreuve de saut en hauteur
Le record du monde est détenu par le Cubain Javier Sotomayor avec le
franchissement d’une barre à 2,45 m le 27 juillet 1993.
Lors de sa course d’élan rectiligne à vitesse constante v=6,8 m / s, il
pousse un cri pour s’encourager. Ce cri est assimilable à une onde
sonore (vitesse du son dans l’air c=340 m / s) de fréquence f=440 Hz)
25) Les spectateurs
percevront alors le cri avec une fréquence :
Le sauteur s'éloigne des spectateurs :
f
' = f c / (c+v) où f ′ est la fréquence sonore perçue par
l’observateur.
f ' = 440 x340 /(340+6,8) ~431 Hz. Réponse
B.
On considère un sauteur en hauteur, assimilé à son centre de gravité G,
de masse m=80 animé d’une vitesse initiale v0=8 m/s et
faisant un angle a=40°
avec la verticale. A l’instant t= 0 𝑠 le sauteur se trouve au niveau
du sol, à une distance d=3,0 m de l’origine du repère. Il essaye alors
de franchir la barre située à une altitude h=2,20 m.
26) Les coordonnées
de l’accélération du sauteur en hauteur sont :
Le sauteur n'étant soumis qu'à son poids, la seconde loi de Newton
conduit à :
ax = 0 ; az = -g. Réponse B.
27) Les
coordonnées de la vitesse du sauteur en hauteur sont alors :
La vitesse est une primitive de l'accélération :
vx = Cste = v0 sin a ;
vz
= -gt +Cste = -gt +v0 cos a ; Réponse D.
28) Les coordonnées
de la position du sauteur en hauteur sont alors :
La position est une primitive de la vitesse.
x =v0
sin a t + cste = v0
sin a t -d.
z = -½gt2 +v0
cos a t ; Réponse A.
29) Lors de ce saut
le sauteur passe :
t =(x+d)
/ (v0
sin a)
avec x = 0 ( origine du repère).
Repport dans z : z = -½gd2
/ (v0
sin a))2
+d / tan a.
z = -5 x9 /(8 sin40)2 +3 / tan(40) = -1,7 +3,6 =1,9 m ( en
dessous de la barre). Réponse B.
Lancer de marteau.
La technique de lancer comporte toujours trois phases :
- La mise en rotation du boulet, pendant laquelle le mouvement du
boulet est circulaire accéléré dans le référentiel terrestre
- Une phase de stabilisation pendant laquelle le mouvement est
circulaire uniforme dans le référentiel terrestre
- La phase d’expulsion pendant laquelle le mouvement est curviligne
accéléré dans le référentiel terrestre
Le référentiel terrestre est supposé galiléen.
Au cours de la phase de stabilisation, le poids du boulet ainsi que
toute autre force est négligeable devant la force appliquée par le
filin. On peut donc considérer que le boulet n’est soumis qu’à la seule
force du filin F=14 000 N, représentée et supposée constante lors de ce
mouvement.
30) On considère le
lancer d’un boulet de masse m au cours duquel la vitesse du boulet lors
de la phase de stabilisation a pour valeur
constante v=45 m /s. Lors de cette phase, dans le repère de Frenet,
l’accélération :
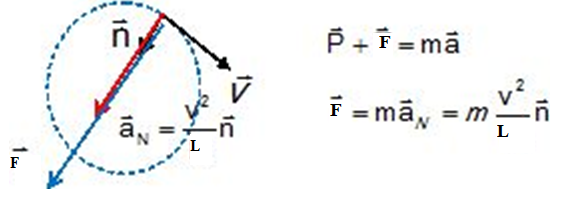
Réponse B.
31) L’expression de
la période de rotation T du boulet lors de la phase de stabilisation
est alors :
Le boulet décrit la circonférence 2pR à la vitesse V en T
seconde.
2p L = V T ; T = 2p L / V.
T2 = 4 p2
L2 / V2 = 4 p2 L2
m / (LF) =4 p2 L / F ; T
= 2 p (mL / F)½.
Réponse A.
32) Les 3 tours
effectués par le boulet de masse m=7 kg lors de cette phase dureront
environ
T = 2p L / V=6,28 x 1,2 /
45=0,167 s.
0,167 x3
=0,5 s.
Réponse B.
On étudie le lancer du boulet après la phase d’expulsion. À la fin de
la phase d’expulsion, le boulet est éjecté à l’instant t=0 𝑠 d’une
hauteur H=1,8 𝑚 et avec une vitesse initiale vi = 27m /s
et
faisant un angle ß=45° avec l’horizontale. On étudie le vol du boulet
soumis à l’unique force exercée par la Terre dans le référentiel
terrestre supposé galiléen et muni d’un repère orthonormé (xOz).
33) L’équation de
la trajectoire du boulet est :
Ox axe horizontal orienté vers la droite ; Oz axe vertical orienté vers
le haut. Origine au sol.
ax = 0 ; az = -g.
Vitesse, primitive de l'accélération : vx = vi
cos ß ; vz = -gt +vi
sin ß.
Position, primitive de la vitesse : x = vi
cos ß t ; z = -½gt2 +vi
sin ß +H.
t = x / ( vi cos ß), repport
dans z :
z = -½gx2 / ( vi
cos ß)2+ tan ß x + H. Réponse B.
34)
La portée du lancer, c’est-à-dire la distance pour laquelle le boulet
atteint le sol, est donnée par :
Au sol z = 0 : -½gx2
/ ( vi cos ß)2+
tan ß x + H = 0.
Discriminant D = tan2ß +2Hg/ ( vi
cos ß)2= [sin2ß
+2Hg / vi
2] / cos2ß.
On retient la racine positive :
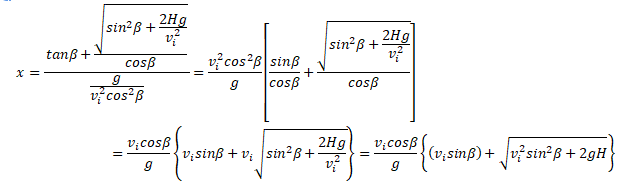
Réponse D.
35. La portée
réelle sera différente de la portée précédente.
Elle sera plus grande si on tient compte du poids et de la possée
d'Archimède et plus faible si on prend en compte le poids et les
frottements.
Réponse C.
36. Valeur de la
poussée d'Archimède exercée sur e boulet :
Volume du boulet V = 9 10-4 m3.
Masse volumique de l'air : rair=1,3
kg m-3.
g rair g = 10 x1,3
x 9 10-4=~1,2 10-2 N. Réponse A.
Epreuve
de voile.
37. La houle est
une onde mécanique transversale. Réponse
C.
38. La fréquence de
la houle est :
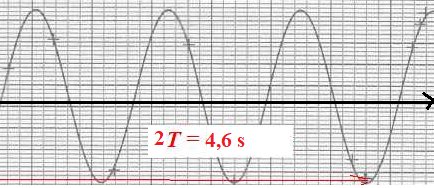
T = 23 s ; fréquence f = 1 / T = 1 / 2,3 ~0,44 Hz. Réponse B.
39. La vitesse de
la houle étant de 36 km /h soit 36 / 3,6 = 10 m/s, sa longueur d'onde
vaut :
l = v
T= 10 x2,3 ~ 23 m. Réponse A.
40. Cette houle
provoque un phénomène de diffraction à l'ouverture d'un port de largeur
a = 46 m.
tan q = l / a = 23 / 46 ~ 0,5.
q ~27
° Réponse
A.
,
|
|
=
|
|