La
plongée sous-marine.
Concours Caplp maths sciences 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Partie A- un exercice de plongée.
La plongée sans bouteille.
On considère un repère dont l'axe Oz est vertical descendant et dont l'origine O est à la surface de la mer.
1. Montrer que la pression à la profondeur z est P(z) = P0 + r gz.
Equation de la statique des fluides : P(z) - P(z=0) = r gz.
P(z) =P(z=0)+ r g z.
2. On entend dire que la pression augmente de 1 bar lorsque la profondeur augmente de 10 m. Vérifier cette affirmation.
P(z=10) - P(z=0) = 1,02 103 x9,8 x10 =9,99 104 ~ 105 Pa ~ 1 bar.
A
la surface le plongeur gonfle ses poumons, bloque sa respiration et
plonge sans relâcher d'air. On suppose que la température de l'air dans
ses poumons est indépendante de z et du temps et que la pression de
l'air dans ses poumons est identique à celle de l'eau qui l'entoure.
3. Exprimer le volume V(z) de la cage thoracique du plongeur à la profondeur z. On donne V(z=0) = 6,0 L.
P(z) V(z) = n R T(z) = constante = P(z=0) V(z=0).
V(z) = P(z=0) V(z=0) / (P(z=0)+ r g z ).
Le plongeur reste immobile à la profondeur z. Pour cela il doit porter un lest de masse mL.
4. 5 Effectuer un schéma des forces sur le plongeur lesté à l'équilibre à la profondeur z. Exprimer chacune de ces forces.
On note m = 80 kg la masse du plongeur non lesté ; volume total du plongeur VT(z) = V0 + V(z) = 77,0 + V(z).
Le plongeur est soumis à son poids P = (m + mL) g, vertical vers le bas et à la poussée d'Archimède, verticale vers le haut, opposée au poids : F = r g VT(z) .
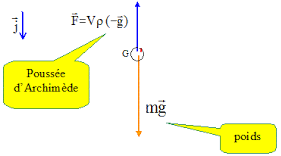
6. Exprimer puis calculer mL si z = 6 m.
(m + mL) g = r g VT(z) ; m + mL = r VT(z) ; mL = r VT(z) - m.
VT(z)= 105 x 6 10-3 /(105 +1,02 103 x9,8 x6) + 77 10-3=8,075 10-2 m3.
mL =1,02 103 x8,075 10-2 -80~2,4 kg.
7. Proposer une explication de l'écart entre la valeur calculée et celle de la masse de lest conseillée ( 8 kg ).
Il
faut emporter suffisament de lest pour ne passe faire tirer vers la
surface lors des paliers de sécurité pour la décompression du plongeur.
Plongée avec bouteille.
8. Indiquer
la valeur de la profondeur limite pouvant être atteinte lors d'une
plongée avec une bouteille d'air comprimé sans risque pour la
santé.
Si le plongeur respire un mélange gazeux dont la pression partielle en
dioxygène dépasse 1,6 bar, son système nerveux est perturbé. Pression
correspondante de l'air : 1,6 x 5= 8,0 bar = 8,0 105 Pa..
P(z) = P0 +r g z < 8,0 105.
r g z < 7,0 105.
z < 7,0 105 / (9,81 x1,02 103) ; z < 70 m.
La narcose apparaît lorsque la pression partielle en diazote dans l’air inhalé dépasse 4 bar.
Pression de l'air : 4 / 0,8 = 5 bar.
z < 4,0 105 / (9,81 x1,02 103) ; z < 40 m.
Depuis
les années 1990, certains plongeurs utilisent un mélange enrichi en
dioxygène, appelé Nitrox. Sur une bouteille, on lit par exemple «
Nitrox 36/64 », ce qui signifie que le mélange est composé de 36 % de
dioxygène et de 64 % de diazote.
9. Donner les avantages et les inconvénients de l’utilisation d’un tel mélange. Une discussion chiffrée sera appréciée.
Si
le plongeur respire un mélange gazeux dont la pression partielle en
dioxygène dépasse 1,6 bar, son système nerveux est perturbé. Pression
correspondante de l'air : 1,6 / 0,36= 4,40 bar = 4,4 105 Pa.
P(z) = P0 +r g z < 4,4 105.
r g z < 3,4 105.
z < 3,4 105 / (9,81 x1,02 103) ; z < 34 m.
La narcose apparaît lorsque la pression partielle en diazote dans l’air inhalé dépasse 4 bar.
Pression de l'air : 4 / 0,64 =6,25 bar.
z < 5,25,0 105 / (9,81 x1,02 103) ; z < 53 m
On pourra plonger plus profond.
Efficacité de la décompression
Pour
vérifier la bonne décompression après la remontée, il est possible
d’évaluer la quantité et la taille des bulles de diazote restantes dans
l’organisme du plongeur à l’aide d’un dispositif utilisant l’effet
Doppler. Le principe de la mesure est donné.
On étudie une situation correspondant aux données suivantes :
– fréquence des ultrasons émis : f0 = 5,0 MHz ;
– célérité des ultrasons : c = 1500 m ⋅ s−1 ;
– angle Doppler : q = 12° ;
– diamètre des bulles : d = 40 μm ;
– vitesse des bulles : v = 35 cm ⋅ s−1.
10. Montrer que les bulles sont bien de petite taille devant la longueur d’onde de l’onde utilisée.
l = c / f =1500 / (5 106)=3 10-4 m= 300 µm >> 40 µm.
11. Déterminer la valeur de la variation de fréquence
Df pour les bulles de la situation étudiée.
Conclure sur la possibilité d’écoute, par une personne formée, d’un signal à cette fréquence.
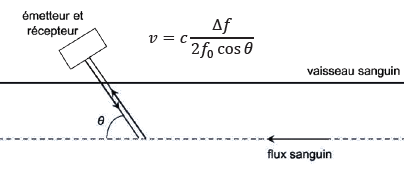
Df = 2 f0 v cos q / c =2 x 5,0 106 x 0,35 x cos12 / 1500 ~2,3 103 Hz, valeur du domaine audible pour l'homme..
12. Citer des utilisations pratiques s’appuyant sur l’effet Doppler.
Mesures de vitesse d'un véhicule, des étoiles, du flux sanguin dans les artères.
|
...
|
....
| L’équipement du plongeur.
Dans cette partie sont évoqués quelques aspects de l’équipement du plongeur.
La matière usuelle des combinaisons de plongée : le néoprène
La température de l’eau en profondeur est telle que le risque
d’hypothermie n’est pas négligeable. Pour se protéger, les plongeurs
portent des combinaisons, le plus souvent en néoprène.
13. Donner le nom du monomère en nomenclature IUPAC.
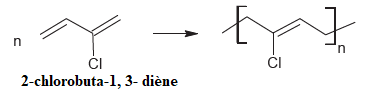
14. Le monomère est
obtenu par déshydrochloration en milieu basique de la molécule de
1,2-dichlorobutan-3-ène. Donner la représentation de CRAM des
stéréoisomères de cette molécule.
15. Indiquer, en
justifiant, la configuration absolue du carbone asymétrique pour chacun
des stéréoisomères précédents. Préciser la relation de stéréoisomérie
entre ces molécules.
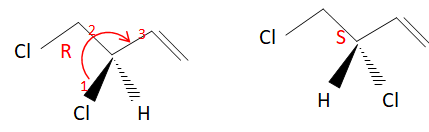
Enantiomères.
16. Donner, en justifiant, la stéréochimie de la double liaison dans le motif du polymère.
Les groupes portés par chaque carbone doublement liés sont classés par priorité décroissante ( règles de Cahn, Ingold, Prelog).
Les groupes prioritaires sont situés du même côté du plan passant par les carbones doublement liés : configuration Z.
17. Déterminer la valeur de la masse molaire d’un échantillon de néoprène de degré de polymérisation moyen 150.
Masse molaire du monomère : 88,5 g / mol.
88,5 x 150 =13 275 g /mol.
Les bouteilles de plongée.
Les bouteilles de plongée sont fabriquées majoritairement en
acier (alliage fer-carbone) ou en aluminium. En milieu marin, elles
sont soumises à un environnement humide et salé qui favorise la
corrosion due au dioxygène dissous. L’oxydation du métal par le
dioxygène dissous entraîne la formation d’oxydes de fer (rouille) et de
cations fer II ou fer III. Pour expliquer le phénomène, on réalise une
expérience avec un clou décrite ci-dessous :
– Déposer dans une boîte de Pétri un clou bien décapé.
– Verser dans la boîte de Pétri un mélange encore tiède de gel
agar-agar, d’eau salée, de phénolphtaléine et d’hexacyanoferrate de
potassium, pour recouvrir entièrement le clou.
– Attendre une quinzaine de minutes que le gel refroidisse et se fige, puis observer.
On rappelle que l’hexacyanoferrate de potassium donne une coloration bleue à la solution en présence d’ions Fe2+(aq)
et que la phénolphtaléine se colore en rose en milieu basique
1. Les couples redox utiles pour les explications sont les suivants :
Fe(aq)2+ / Fe(s) et O2(g) / HO(aq)−.
18. Dire quels sont les ions mis
en évidence aux extrémités et dans la partie centrale du clou. En
déduire les demi-équations redox traduisant les transformations ayant
lieu dans chaque zone, ainsi que l’équation de la réaction
d’oxydoréduction globale se produisant à la surface du clou.
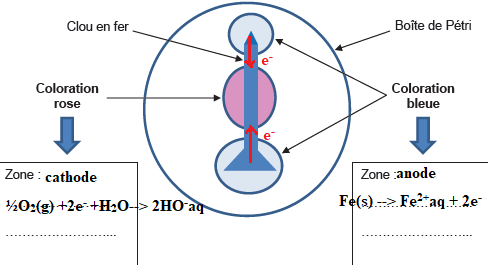
½O2(g) + H2O(l) +Fe(s) --> Fe2+aq +2HO-aq.
Pour
interpréter le phénomène, on considère que le clou se comporte comme
une micropile.
19. Indiquer, dans les encadrés prévus à cet effet les zones anodique(s) et
cathodique(s) ainsi que les zones où se déroulent une oxydation ou une
réduction. Préciser le sens de déplacement des
électrons dans le métal.
Pour protéger une bouteille de plongée de la
corrosion, une entreprise envisage d’utiliser une technique largement
employée dans l’industrie pour protéger les pièces en acier :
l’électrozincage, c’est-à-dire le dépôt électrolytique de zinc à la
surface de l’acier. Une fois déposé sur la pièce, le zinc, plus
réducteur que le fer, s’oxydera à sa place.
Un technicien teste au préalable l’électrozincage
d’une plaque carrée d’acier de côté a = 10 cm et d’épaisseur
négligeable. Il plonge cette première électrode et une plaque de zinc
(seconde électrode) dans une solution de sulfate de zinc (Zn(aq)2+ + SO4(aq)2− ). Ensuite, il réalise l’électrolyse de la solution en imposant un courant d’intensité I = 2,0 A à l’aide d’un générateur.
20. Schématiser le
dispositif d’électrozincage complet en plaçant l’appareil de mesure
permettant de lire l’intensité dans le circuit.
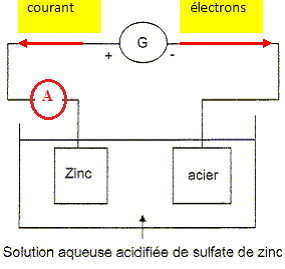
21. Expliquer le principe d’une électrolyse en précisant les conversions d’énergie mises en jeu.
Un
électrolyseur est un récepteur : il reçoit de l'énergie électrique
qu'il convertit en énergie chimique et en énergie thermique.
Le technicien souhaite protéger l’ensemble de la pièce en acier en réalisant un dépôt d’épaisseur d = 20 μm = 2,0 10-3 cm.
Données :
– constante de Faraday : F = 9,6 × 104 C ⋅ mol−1 ;
– masse volumique du zinc : rZn = 7,14 g ⋅ cm−3 ;
– masse molaire du zinc : M(Zn) = 65,4 g ⋅ mol−1.
22. Montrer que la durée Dt de l’électrolyse pour effectuer l’électrozincage vérifie la relation suivante :
Volume du zinc déposé : 2d a2= 2 x 2 10-3x 102 =0,4 cm3.
Masse de zinc : 2d a2 rZn=0,4 x 7,14=2,856 g.
Quantité de matière de zinc : 2d a2 rZn / M(Zn) =2,856 / 65,4=0,0437 mol.
Quantité de matière d'électrons : 4 d a2 rZn / M(Zn) = 2 x0,0437=0,0873 mol.
Q = 4 d a2 rZn / M(Zn) F = I Dt = 0,0873 x9,6 104=8,38 103 C.
Dt =4 d a2 rZn F/ ( IM(Zn))= 8,38 103 / 2~4,2 103 s ou environ 1,2 heures.
23.
Proposer, à la lumière de ce qui précède, une analyse critique de la
technique d’électrozincage envisagée par l’entreprise pour protéger une
bouteille de plongée de la corrosion. Tout élément de discussion
concret et chiffré sera apprécié.
Faible épaisseur de la couche de zinc, la taille de la pièce augmente peu.
Procesus réalisé à température ambiante, en évitant toute déformation des métaux.
Processus plus économique qu'une couche de peinture.
Belle finition esthétique.
Une crème solaire de rigueur.
Lors d’une plongée peu profonde, le plongeur doit utiliser de la crème
solaire s’il ne porte pas de combinaison car une exposition prolongée
aux rayonnements UV peut entraîner des dommages au niveau de la peau
pouvant aller jusqu’au développement de cancers.
Les crèmes solaires fonctionnent grâce à des filtres UV organiques ou
minéraux. On s’intéresse dans cette partie à une crème dont le filtre
organique est l’avobenzone.
L'avobenzone existe à l’état fondamental sous la forme d'un mélange des formes énol et cétone, favorisant généralement l'énol.
24. À l’aide d’un
schéma, proposer une explication du fait que la forme énol de
l’avobenzone est généralement favorisée par rapport à la forme cétone.
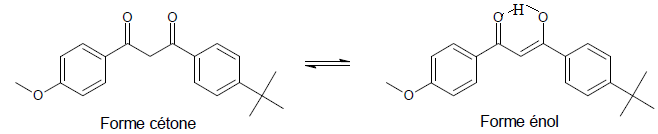
Plus grande délocalisation des électrons dans la forme énol.
En première approximation, un filtre UV est considéré efficace à une
longueur d’onde donnée lorsque son coefficient d’absorption molaire e est supérieur à 104 L⋅cm−1⋅mol−1.
Pour calculer ce coefficient dans le cas de l’avobenzone, on prépare
dans un premier temps une solution mère de concentration C0=1,00×10−4 mol⋅L−1
en avobenzone dans le propan-2-ol. Ensuite, on prépare plusieurs
solutions filles de concentrations C connues en avobenzone dans le
propan-2-ol. On mesure enfin leur absorbance A dans une cuve de 1 cm de
côté à une longueur d’onde de 357 nm (maximum d’absorption de
l’avobenzone). Les résultats sont présentés dans le tableau suivant :
Solution fille
|
S1
|
S2
|
S3
|
S4
|
S5
|
Concentration C (µmol / L)
|
5,0
|
10
|
15
|
20
|
25
|
Absorbance A
|
0,14
|
0,27
|
0,41
|
0,55
|
0,68
|
e (L mol-1 cm-1)=A / C
|
2,8 104
|
2,7 104 |
2,7 104 |
2,75 104 |
2,7 104 |
25.
Donner le protocole expérimental pour préparer 100 mL de la solution
fille S4 à l’aide de la solution mère et du matériel usuel d’un
laboratoire de chimie.
Facteur de dilution : 100 / 20 = 5.
Prélever 20 mL de solution mère à l'aide d'une pipette jaugée et verser
dans une fiole jaugée de 100 mL contenant 1 /3 d'eau distillée. Agiter.
Compléter jusqu'au trait de jauge à l'aide d'eau distilée. Agiter pour
rendre homogène.
26. Rappeler la loi de la
spectrophotométrie utile pour exploiter ces résultats en précisant son
nom usuel et en explicitant la signification physique de chaque terme.
Loi de Beer-Lambert.
A= log (I0/I) = elc ( A est l'absorbance ou densité optique)
Cette loi est vérifiée lorsque la solution est de concentration inférieure à : c < 0,1 mol.L-1.
e (L mol-1 cm-1) est une caractéristique de la molécule. Plus e sera grand, plus la solution absorbe.
l est l'épaisseur de la cuve (cm) et c la concentration de la solution (mol/L).
27. Proposer une raison plausible du choix de concentrations relativement faibles en avobenzone pour les solutions filles.
28. Déterminer
précisément la valeur du coefficient d’absorption molaire de
l’avobenzone en détaillant la méthode utilisée. Conclure sur
l’efficacité du filtre.
2,7 104 > 104 : le filtre est efficace.
La modification de la vision.
Lorsque le plongeur ouvre les yeux sous l’eau, il ne voit pas
nettement. La présence d’eau, dont l’indice de réfraction est proche de
celui du système « cornée – cristallin », entraîne la formation de
l’image de l’objet à l’arrière de la rétine. Le signal véhiculé par le
nerf optique au cerveau correspond à une image floue.
29. Dire à quel défaut de la vue, la vision sous l’eau s’apparente.
Hypermétropie.
On lit souvent qu’avec le masque, les objets paraissent plus près, aux
trois quarts de leur distance réelle au plongeur. On souhaite vérifier
cette affirmation. On suppose que le plongeur observe un poisson situé
au point A..
On néglige l’épaisseur de la vitre.
30. Exprimer puis
calculer l’angle de réfraction r par la vitre du rayon issu du point A
qui parvient, à terme, à l’oeil du plongeur.
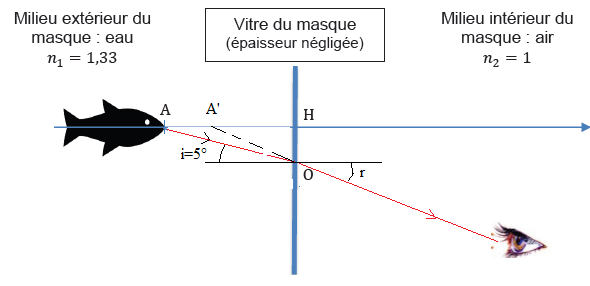
n1 sin 5 = n2 sin r ; sin r = 1,33 sin 5 =0,116 ; r =6,6°
31. Sans souci
d’échelle, tracer l’image A′ du point A à travers le système { eau +
vitre + air }. Indiquer, avec justification, la nature de cette
image.
Cette image est virtuelle.
32. En se plaçant dans l’approximation des petits angles :
tan i ~ i = OH / AH ; tan r ~ r =OH / HA' ; i / r ~HA' / AH.
n1 sin i = n2 sin r s'écrit : n1 i ~ n2 r soit i / r ~ n2 / n1.
HA' / AH ~n2 / n1 ; HA' ~n2 / n1 AH =AH / 1,33 ~ 0,75 AH.
"les objets paraissent plus près, aux trois quarts de leur distance réelle au plongeur " affirmation vérifiée.
La modification de l’ouïe.
Afin de localiser une source sonore, le cerveau analyse notamment
l’écart temporel entre les sons perçus par chaque oreille (différence
interaurale en temps). On se place dans le modèle simplifié du dipôle :
chaque oreille reçoit directement une onde sonore sinusoïdale de
fréquence f émise à l’instant t = 0 par une source, le reste de la tête
et du corps étant absent. La source est suffisamment éloignée pour que
les rayons sonores arrivent aux deux oreilles en étant parallèles sous
un angle q (voir figure).
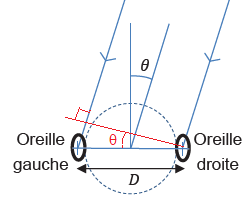
Données :
– célérités du son dans l’air et dans l’eau : cair = 340 m ⋅ s−1 et ceau = 1500 m ⋅ s−1 ;
– distance entre les oreilles : D = 20 cm.
33. Exprimer la différence interaurale en temps Dt en fonction de l’angle d’incidence q, de la distance D entre les oreilles et de la célérité c du son dans le milieu considéré.
Différence des distances parcourues par les deux ondes : D sin q.
Dt =D sin q / c.
34. Montrer qu’une source située à q
= 90° d’un plongeur dans l’eau est interprétée par son cerveau comme
une source à environ 13° dans l’air et que la perception sonore est
donc faussée.
Dans l'eau Dt =0,20 / 1500 =1,33 10-4 s.
Dans l'air : D sin q / c = 1,33 10-4 ; sin q =1,33 10-4 x 340 / 0,2 =0,227 ; q ~13°.
La différence interaurale en temps Dt n’est exploitable par le cerveau que si elle est inférieure à la période du signal reçu.
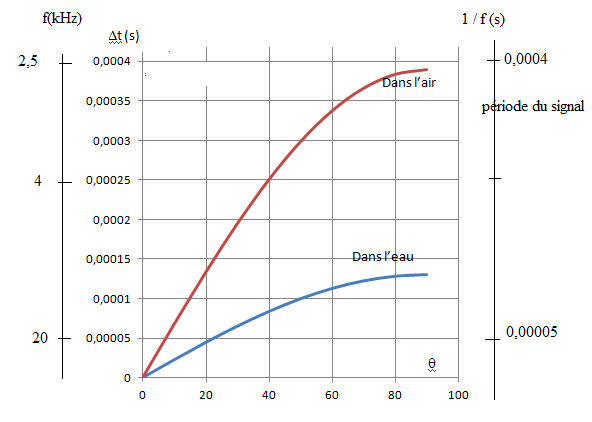
35. Pour chaque
type de milieu de propagation du son, l’air ou l’eau, représenter sur
le graphique le domaine des fréquences f exploitables par le cerveau
selon l’angle d’incidence q. Commenter.
Dans l'eau : Dt =D sin q / c = 0,2 / 1500 sin q =1,3 10-4 sin q.
Dans l'air : Dt =D sin q / c = 0,2 / 340 sin q =3,9 10-4 sin q.
La modification de la température corporelle.
L’hypothermie se manifeste quand la température corporelle
devient inférieure à 35 °C. Au cours d’une plongée, le corps humain se
refroidit car il y a des pertes d’énergie sous forme thermique par
conduction, convection et rayonnement.
36. Rappeler brièvement ce que sont chacun de ces trois modes de transferts thermiques en précisant ce qui les distingue.
Conduction : échange d'énergie avec contact.
Convection : mouvement de molécules dans un liquide ou un gaz..
Rayonnement du soleil dans l'espace.
On considère tout d’abord un plongeur sans combinaison. Son corps, sous
sa peau, est à une température T supposée uniforme et sa capacité
thermique est C=3,0×105 J⋅K−1. Les conditions d’étude sont telles que l’on peut utiliser le concept de résistance thermique : on note Rp=3,0×10−2 K⋅W−1 la résistance thermique de conduction à travers la peau du plongeur et Rc=5,0×10−2 K⋅W−1
la résistance thermique liée aux transferts thermiques générés dans
l’eau par le plongeur (essentiellement par convection et rayonnement).
La plongée est effectuée dans une eau à la température Te=16 °C
(température à distance du plongeur).
37. Expliquer pourquoi la puissance thermique totale Pth dissipée par le plongeur à un instant t s’écrit : Pth=(T-Te) / Req avec Req=Rp+Rc .
Puissance thermique totale = différence de température / résistance thermique totale du plongeur.
38. Le métabolisme fournit au plongeur une puissance thermique Pm=110
W. À l’aide de la question précédente et d’un bilan thermique entre les
instants t et t+dt, montrer que la température T du corps du plongeur
suit l’équation différentielle :
dT / dt + T / t = Tl /t avec t= Req C et Tl= Te+ReqPm.
Variation de l'énergie interne du plongeur durant dT : C dT ; puissance correspondante C dT / dt.
Bilan de puissance : C dT / dt = Pm -Pth=Pm -(T-Te) / Req .
dT / dt = Pm / C -(T-Te) / ( CReq ).
dT / dt +T /(CReq ) =Pm / C+Te / ( CReq )= Pm Req/ (CReq)+Te / ( CReq )=(Te+ReqPm) / ( CReq ).
dT / dt + T / t = Tl /t .
39. Déterminer la solution de l’équation différentielle précédente qui respecte la condition initiale T(0)=T0.
Solution générale de dT / dt + T / t =0 : T = A exp(-t / t) avec A une constante.
Solution particulière T = Tl .
Solution générale : T = A exp(-t / t) + Tl .
A l'instant initial : T0 = A + Tl ; A = T0 - Tl .
T = (T0 - Tl) exp(-t / t) + Tl .
40. La température initiale du corps du plongeur est T0=37 °C. Calculer la valeur de la température du corps au bout de deux heures de plongée. Commenter.
Tl= Te+ReqPm =16+273+8 10-2 x110=297,8 K. t = 8 10-2 x3,0 105=2,4 104 s.
T = (310-297,8) exp(-7200/ 24 000)+297,8 ~307 K ou ~34 °C.
On considère à présent le même plongeur, mais revêtu d’une combinaison en néoprène de résistance thermique Rn=3,0×10−2 K⋅W−1.
41. En utilisant une
modification simple du modèle précédent, à expliciter, calculer la
nouvelle température du corps au bout de deux heures de plongée.
Commenter.
Req=Rp+Rc+ Rn = 0,11 K⋅W−1.
Tl= Te+ReqPm =16+273+0,11 x110=301,1 K.
T = (310-301,1) exp(-7200/ 24 000)+301,1 ~308 K ou ~35 °C.
Le corps se refroidit moins vite.
L’observation des coraux au cours d’une plongée.
Les plongeurs ont remarqué depuis plusieurs années une disparition
progressive des coraux, essentiellement constitués de carbonate de
calcium CaCO3(s). L’une des causes de ce phénomène est
l’augmentation de l’acidité des océans en raison des gaz à effet de
serre présents dans
l’atmosphère, en particulier du dioxyde de carbone CO2(g) : celui-ci se dissout dans l’eau de mer pour donner de l’acide carbonique H2CO3(aq) qui est un diacide.
Au cours des 300 dernières années, le pH des océans a diminué de 0,1 unité pour être maintenant aux alentours de 8,1.
Données :
– Concentration standard :c° = 1 mol ⋅ L−1.
– Couples de l’acide carbonique et valeurs de pKA à 25 °C :
H2CO3(aq) / HCO3-(aq) : pKA1 = 6,3 ;
HCO3-(aq) / CO32-(aq) : pKA2 = 10,3.
– Produit de solubilité du carbonate de calcium à 25 °C : pKS = 8,3.
42. Placer sur un
diagramme les domaines de prédominance des différentes espèces et
en déduire l’espèce majoritaire dans les océans. Donner la
particularité des ions hydrogénocarbonates.
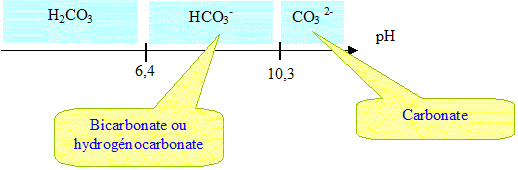
HCO3-(aq) prédomine à pH = 8,1. HCO3-(aq) est amphotère.
43. Expliquer
pourquoi une plus grande quantité de dioxyde de carbone atmosphérique
entraîne l’acidification des océans en explicitant l’équation
pertinente de réaction de l’acide carbonique H2CO3(aq) avec l’eau.
H2CO3(aq) + H2O(l) = HCO3-(aq) +H3O+aq.
H3O+aq est libéré et le pH diminue.
44. Déterminer la valeur du pourcentage d’augmentation de la quantité d’ions H3O+aq correspondant un abaissement du pH de 0,1 unité.
H3O+aq augmente de 10-0,1 ~0,8 mol/ L.
45. Donner l’équation de la réaction de dissolution du carbonate de calcium CaCO3(s) dans l’eau, ainsi que l’expression du produit de solubilité KS associé à celle-ci.
Dans l’eau de mer, la solubilité du carbonate de calcium est s = [Ca2+(aq) ] ~ [HCO3-(aq) ].
46. Montrer que :
pS =½(pH+pKs-pKa2).
CaCO3 (s) = Ca2+ (aq) + CO32- (aq).
Expression du produit de solubilité du carbonate de calcium.
Ks = [Ca2+aq][CO32-aq].
A pH compris entre 7,3 et 9,3, HCO3- ] prédomine ;
CO2(aq) et CO32- sont négligeables.
Ka2 = [CO32-aq] [ H3O+aq ] / [HCO3- ]
Ks = [Ca2+aq][HCO3- ] = [Ca2+aq] KA2 [HCO3- ] / [ H3O+aq ]= s2KA2 / [ H3O+aq ].
s2 = Ks [H3O+] / Ka2.
2 log(pS) = log(Ks) +log( [H3O+])-log (Ka2).
-2 log(pS) = -log(Ks) -log( [H3O+])+log (Ka2).
2pS =pH-pKa2+pKs.
47. En déduire la
valeur de la quantité de matière supplémentaire de carbonate de calcium
dissous par litre d’eau lorsque le pH passe de 8,2 à 8,1. Identifier le
problème pour les coraux.
pS initial =½(8,2+8,3-10,3)=3,1. [S]=7,9 10-4 mol / L.
pS final =½(8,1+8,3-10,3)=3,05. [S]=8,9 10-4 mol / L.
La solubilité du carbonate de calcium augmente et le squelette du corail devient plus fragile.
En toute rigueur, s = [Ca2+(aq) ] = [H2CO3(aq)] + [HCO3-(aq)] + [CO32-(aq) ].
48. Tracer sur ce
document réponse la courbe obtenue avec le résultat démontré à la
question 46. et comparer les deux graphiques par zones.
Question 46 : pS = ½(pH+8,3-10,3) =0,5 pH-1.
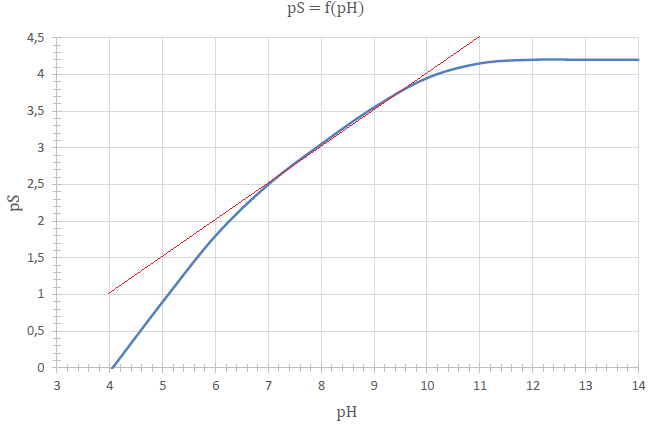
pH compris entre 7 et 10 : courbes identiques.
|
ir
|
|
|