Oscillation
d'une tige rigide,
Concours ENAC 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Une tige homogène T, de masse m et de longueur MN = 3b, est initialement à l’équilibre avec une position horizontale dans le
champ de pesanteur. On l’astreint à tourner autour d’un axe horizontal (KD)
fixe dans le référentiel du laboratoire (supposé galiléen) et
orthogonal à T et donc au plan de la figure. L’axe de rotation, orienté
positivement vers le lecteur, sépare la tige en deux parties de
longueurs MK = 2b et KN = b. Les frottements sont négligés. Le moment
d’inertie de T par rapport à D vaut mb2. L’extrémité
M (gauche) de la tige est fixée à un ressort vertical, de raideur K et de longueur à vide l0. L’autre extrémité du ressort est
solidaire d’un bâti, fixe dans le référentiel du laboratoire. La coordonnée x de M est repérée par l’axe Ox. Initialement, M
coïncide avec l’origine O du repère, et donc x(t = 0) = 0.
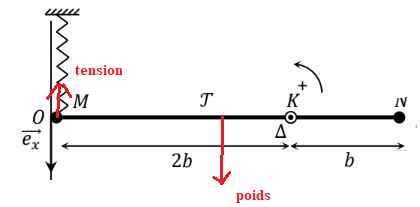
1. Exprimer le moment MD(P) (scalaire) du poids de la tige par rapport à l’axe orienté KD, à l’instant initial :
Le poids a tendance à faire tourner la tige dans le sens positif. Il s'applique à la distance ½b de l'axe de rotation.
Le poids est perpendiculaire à la tige.
MD(P) =½mg b.
2. Exprimer la force F qu’exerce le ressort en M à l’instant initial.
Le moment de la force F, orientée vers le haut, doit compenser le moment du poids.
F 2 b = ½mgb ; F = mg / 4.
3. Quelle est la longueur l du ressort à l’instant initial ?
Tension du ressort : F = k(l-l0).
k(l-l0) = m g / 4 ; l-l0 = mg /(4k) ; l = mg /(4k) +l0.
4. On étudie désormais le régime dynamique au voisinage de la position horizontale de T (x << l0). Exprimer le moment
scalaire MD(F) de F par rapport à l’axe orienté KD :
x << l0) : la tension du ressort est quasiment othogonale à la tige.
F = k (l+x-l0).
F a tendance à faire tourner la tige dans le sens négaitif.
MD(F) = - F 2 b= - k (l+x-l0) 2 b = - k (l+x-l0) 2 b = - k( mg /(4k) +x) 2b = -½mg b-2kbx.
|
...
|
....
|
5. L’équation différentielle d’évolution de l’abscisse x(t) de M se met sous la forme suivante :
x" +w02x=0.
où w0 est une constante temporelle. Exprimer w0.
Théorème du moment cinétique :
JD q" =MD(P) +MD(F).
mb2q" =½mgb -½mg b-2kbx = -2Kbx.
mbq" =-2Kx ; q" =-2K / (mb) x.
tan q = x / (2b) ~q.
x" / (2b) ~q".
x" / (2b) +2K / (mb) x=0.
x" +4K/m x=0.
w02= 4 K / m.
6. Exprimer l’énergie cinétique Ek de T, au voisinage de sa position horizontale.
Energie cinétique d'un solide en rotation : Ek = ½JD q'2.
JD = mb2 ; x / (2b) ~q ; q' = x' / (2b).
Ek =½mb2x'2 / (4b2).
Ek = m x'2/ 8.
|
ane.
|
|
|