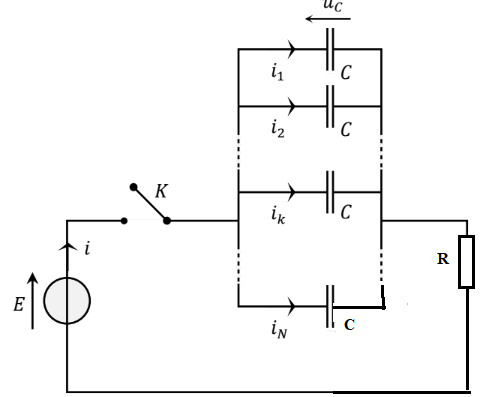
Régime transitoire d'un ensemble de condensateurs, Concours ENAC 2024. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... On associe, en dérivation, un ensemble de N condensateurs identiques de capacités C. Le dipôle obtenu est alors monté en série avec un résistor de résistance R, un générateur de tension continue de force électromotrice (tension) E, et un interrupteur K que l’on ferme à un instant pris comme origine temporelle (t = 0). On note i l’intensité du courant électrique débité par le générateur et ik, k allant de 1 à N, l’intensité du courant électrique dans le k-ième condensateur. On désigne uC la tension aux bornes des condensateurs. Avant la fermeture de K (t < 0) ∶ uC(t) = U0 où U0 est la tension de charge des condensateurs. . 1. Que vaut l’énergie totale e0 emmagasinée par les condensateurs, avant la fermeture de K ? Les condensateurs en dérivation sont équivalents à un condensateur unique de capacité Céqui=N C. e0 = ½NC U02. 2. Que peut-on affirmer lorsque t > 0 ? La loi des mailles s'écrit : E = Ri + uC. i = dq/dt = Céqui duC/dt ; E = RCéqui duC/dt + uC. Constante de temps t = 1/(RCéqui)=1 /( NRC). Les condensateurs étant identiques, ik = i / N. On dérive E = Ri + uC. 0 = Rdi/dt +dUc/dt. i =Céqui dUc/dt ; 0 = Rdi/dt +i /Céqui  ; di/dt +i / (NRC) =0. i= Nik ; Ndik/dt +ik/(RC) = 0.  3. Comment évolue uC(t) après la fermeture de K ? Solution générale de RCéqui duC/dt + uC=0 : uC(t) = A exp(-t /(NRC)) avec A une constante réelle. Solution particulière de l'équation différentielle uC = E. Solution généraale de cette équation : uC(t) =E + A exp(-t /(NRC)). uC(t=0) = E+A = U0 ; A = U0-E. uC(t) =E + (U0-E) exp(-t /(NRC)). ... .... 5. Quel est le courant i(0+) débité par le générateur en t = 0+ ? Loi des mailles : E = U0+R i(0+)  ; i(0+)  =(E-U0) / R. 6. Comment évolue ik(t) après fermeture de K ? Solution de l'équation différentielle : Ndik/dt +ik/(RC) = 0. ik(t) = B exp(-t/(NRC))=B exp(-t / t) avec B une constante. ik(t=0+) = i(0+) / N = (E-U0) / (RN) ; ik(t) = (E-U0) / (RN)exp(-t / t).

menu