Physique
chimie.
Concours Ecole de Santé des Armées 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Saut en parachute.
Un
moniteur s'associe avec la personne qui saute pour la première fois
pour former un tandem. On étudie la nature du mouvement du tandem.
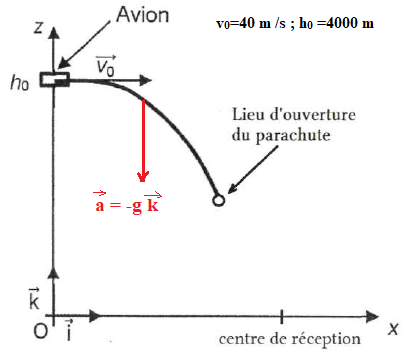
1. Donner l'expression du vecteur accélération du tandem durant la chute libre.
Coordonnées du vecteur accélération ( 0 ; -g).
2. Donner l'expression du vecteur vitesse du tandem durant la chute libre.
Coordonnées du vecteur vitesse, primitive du vecteur accélération : (v0 ; -gt).
3. Donner l'expression du vecteur position du tandem durant la chute libre.
Coordonnées du vecteur position, primitive du vecteur vityesse :
x =v0 t ; z = -½gt2 +h0.
L'ouverture du parachute est prévue à l'altitude zouverture = ½h0.
4. Montrer que xouverture =(h0 / g)½ v0 et faire le calcul. Quelle est la durée de la chute libre ?
½h0=-½gt2 +h0 ; h0=gt2 ; t = (h0 / g)½ ;
xouverture =v0 t =(h0 / g)½ v0 = (4000 / 10)½ x40=20 x40=800 m.
Durée de la chute libre : (h0 / g)½ =(4000 / 10)½ = 20 s.
5.
Après l'ouverture le tandem ne descend pas à la verticale, mais subit
une dérive linéaire selon l'axe Ox dans le sens du vecteur vitesse
initiale.
Dx : variation de l'abscisse ; Dz : variation de l'altitude ; Dx / Dz = -0,10.
Calculer l'abscisse du centre de réception à terre..
Si Dz = -1 m, Dx =0,1 m.
Quand l'altitude diminue de 1 m, l'abscisse augmente de 0,1 m.
Quand l'altitude diminue de 2 000 m, l'abscisse augmente de 200 m.
Ajouter xouverture : 800 +200 = 1 000 m.
Exercice 2
Le
diamètre normal d'une hématie est de 7 à 8 µm. Certaines hématies
subissent un grossissement anormal et atteignent une taille de 12 µm.
Pour les étudier, on utilise un tamis calibré pour les retenir.
On utilise un laser de longueur d'onde l = 500 ±1 nm et on cherche à le tester. On utilise le montage suivant :
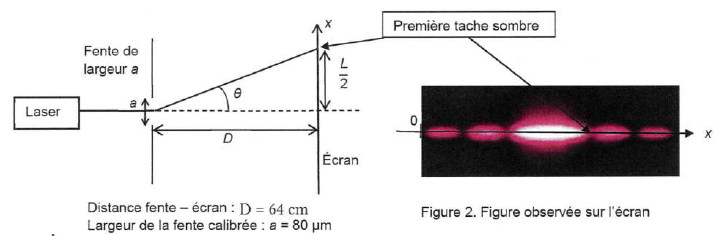
a. Nommer le phénomène physique à l'oeuvre.
La diffraction.
b. Exprimer q en fonction de L, largeur de la tache centrale et D.
tan q = L / (2D) ~ q si cet angle est petit.
c. Exprimer la longueur d'onde en fonction de L, a et D.
q = l / a = L / (2D) ; l = a L /(2D).
On remplace l'écran par une caméra qui permet d'obtenir l'intensité lumineuse relative en fonction de la positin x.
L'origine x = 0 est prise sur le bord du capteur de la caméra. Calculer la longueur d'onde du laser.
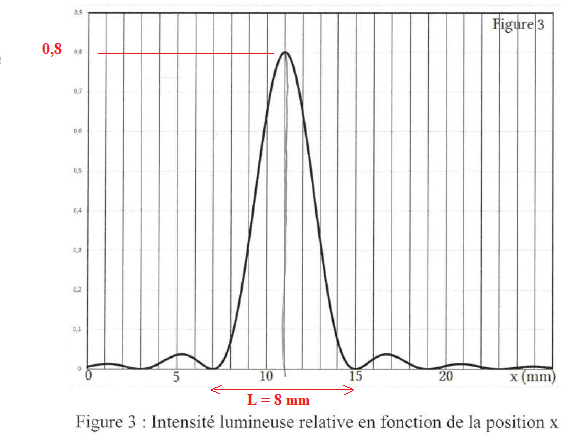
l = a L /(2D)=80 10-6 *8 10-3 / (2 x0,64)=5 10-7 m.
2. On réalise une exprérience d'interférences pour vérifier les dimensions du tamis en utilisant la diode laser précédente.
La largeur du fil plastique constituant le tamis est égale à 100 µm et l'ouverture de la maille carrée est notée a.
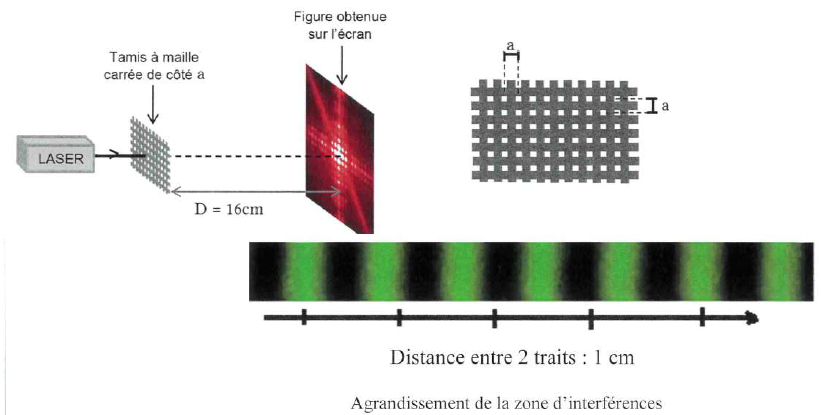
a. Déterminer la valeur de l'interfrange i et en déduire a.
5 interfranges = 5 i = 4 cm = 0,04 m.
i = 0,04 / 5 = 8 10-3 m.
i = l D / a ; a = l D / i = 500 10-9 x0,16 / (8 10-3) =1,0 10-5 m = 10 µm.
Ce tamis est efficace pour filtrer les hématies anormales.
|
...
|
....
|
Exercice 3 QCM.
1. Soit une lunette astronomique dont l'objectif a pour vergence +0,25 dioptrie et l'oculaire pour distance focale image + 10 mm.
A. Une lunette astronomique est un système afocal. Vrai.
B. Une lunette astronomique est composée de deux lentilles convergentes. Vrai.
C. La distance focale objet de l'objectif vaut 4 m. Faux.
Distance focale image de l'objectif = 1 / 0,25 = 4 m.
.D. La distance focale objet de l'objectif vaut -4 m. Vrai.
E. La vergence de l'oculaire vaut 100 dioptries. Vrai.
1 / (10 10-3) = 100 dioptries.
2. Lois de Kepler.
Pour un même astre attracteur de masse M, la troisième loi de Kepler indique T2/a3 = Cste avec T période de révolution et a le demi-grand axe de l'ellipse.
A. La constante dépend de la masse du satellite. Faux.
B. La vitesse v d'un satellite autour de cet astre attracteur a pour expression v = (GM / a)½. Vrai.
D. La troisième loi de Kepler s'écrit : T2/a3 = 4p2 / (GM) Vrai.
C et E écritures fausses de la troisième loi de Kepler.
Loi des gaz parfaits.
La température de l'air d'un pneu qui a roulé est de 47°C. Le volume
d'air contenu dans le pneu est de 40 L et la pression vaut 3,2 bar.
L'air est considéré comme un gaz parfait.R = 8 J K-1 et 47 / 15 ~ 3.
3. La quantité de matière d'air contenu dans le pneu vaut 2 moles.
n = PV / RT = 3,2 105 x 0,040 / [8 x (273+47)] = 3,2 103 / (2 x320)=10 /2 = 5 moles. Réponse D.
4. A une température ambiante de 15 °C, pour le même volume d'air, la pression du pneu est :
P = nRT / V = 5 x 8 x(273+15) / 0,04 =40 x288 / 0,04 = 1000 x288 =2,88 105 Pa = 2,88 bar. Réponse D.
5. Dipôle RC série.
L'équation différentielle de la tension uc(t) aux bornes du condensateur initialement déchargé, chargé par un générateur de tension idéal est :
10-3 duc/dt +uc =5.
A. L'unité du second membre est l'ampère. Faux.
Le second membre est homogène à une tension ( volt).
B. la constante de temps t vaut 1 ms. Vrai.
duc/dt +1 / t uc =5 / t.
t = 103 s = 1 ms.
C. la constante de temps t vaut 103 s. Faux.
D La forme de la réponse de la tension uc(t) est donnée par la figure b. Vrai.
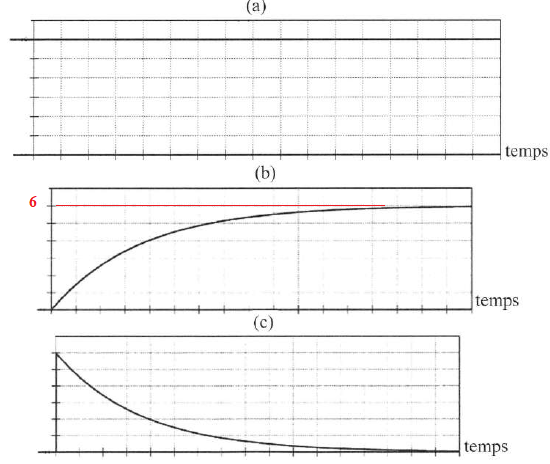
E. uc(t) = 5 (1-exp(-1000 t). Faux.
uc(t) = 6(1- exp(-1000 t)).
6. Thermodynamique.
La peau d'un avant bras d'un brûlé est modélisée par un parallélépipède de longueur 30 cm, de largeur 5 cm, d'épaisseur 2 cm.
Masse volumique de la peau r = 1000 kg m-3 ; capacité thermique massique C = 4 kJ kg-1 K-1.
La peau est considérée comme un système incompressible.
La capacité thermique de la peau brûlée vaut environ :
Volume : 0,30 x 0,05 x0,02 = 3 10-4 m3.
Masse : 3 10-4 x1000 = 0,3 kg.
Capacité thermique : 4 x0,3 = 1,2 kJ K-1. Réponse C.
La température de la peau brûlée atteint la température Tf = 326 K et que la température de surface de la peau valait 306 K, montrer que la chaleur emmgasinée par la peau vaut 24 kJ.
Capacité thermique fois différence de température = 1,2 x 20=24 kJ.
|
|