Suites
récurrentes, polynômes sympathiques, concours général maths 2023.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice
1 : soyons rationnels.
Pour tout entier
n > 1, on note
v(n) le plus grand entier k tel que n /2k soit un entier.
On définit la suite (un)n>1 par récurrence,
en posant u1 = 1 puis, pour tout entier n >2,
un=0 si un-1=0 ;
un=1+2v(n)-1/(un-1) si un-1
diffère de zéro.
1) Donner la valeur
des entiers v(1), v(2), v(3) et v(4).
1/ 20=1 ; v(1)=0.
2 /21=1
; v(2)=1.
3 / 20=3 ; v(3)=0.
La valeur de v( nombre impair) est toujours nulle : v(5) =0.
4 / 22=1
; v(4)=2.
2) Démontrer, pour
tout entier n >1,
que v(n) = 0 si n est impair et que v(n) = v(0,5n)+1 si n est pair.
n / 20= n entier naturel
Si k entier naturel non nul : 2k est pair ; si n est impair
alors n / 2k n'est pas un entier naturel et v(n) = 0.
Soit n pair et notons v(n) = k0.
n / 2k0 entier naturel et n / 2k0+k n'est pas un
entier naturel.

Par conséquent v(n / 2) = k0-1 soit v(n) = v(n / 2) +1.
3) Calculer les
huit premiers termes de la suite (un)n>1 et vérifier que
u8 = 4.
u1 = 1.
u2 =1+2v(2)-1/1=1+2-1=2.
u3 = 1+2v(3)-1/ 2=1+0-0,5=0,5.
u4=1+2v(4)-1/0,5=1+4-2=3.
u5=1+2v(5)-1/3=1-1/3 = 2 /3.
v(6) = v(3)+1=1 ; u6 = 1+2v(6)-2 /3 =1+2-3 /2=3-1,5=1,5.
v(7)=0 ; u7=1+2v(7)-2/3=1 /3.
v(8) = v(4)+1=2+1=3 ; u8=1+2v(8)-3=1+6-3=4.
4) Démontrer, pour
tout entier n >1,
que un est un nombre rationnel strictement positif, que u2n
= un +1
et que u2n+1 =un / (un +1).
.Démonstration par récurrence.
Initialisation : u1 =1
appartient à Q*+.
u2 = 2=u1+1 est vrai.
u3=0,5 = 1/ 2 = u1/u2 est vrai.
Hérédité :
un appartient à Q*+
; u2n = un +1 et que u2n+1 =un / (un +1).sontt supposés vrais.
Cas 1 :
n+1 est pair, alors il existe un entier naturel p >0 tel que 2p =
n+1.
un+1=u2p=up+1.
up appartient à Q*+ donc un+1
appartient à Q*+.
Cas 2 :
n+1 est impair, il existe un entier p non nul tel que : n+1=2p+1 ; p= n
/ 2 appartient à [1 ; n].
un+1=u2p+1 =up / up+1 ;
up et up+1
appartiennent à Q*+, donc up / up+1
appartient à Q*+.
un+1 appartient à Q*+.
u2n+2=1+2v2n+2-1/u2n+1=
1+2(vn+1+1)-1/u2n+1=3+2vn+1-1/u2n+1= 3+2vn+1-(un+1)/un.
1+2vn+1+1-1/un=[1+2vn+1-1/un]+1=un+1+1.
L'hérédité
est démontrée.
Conclusion
: la propriété est vraie au rang 1 et
héréditaire, elle est donc vraie
pour tout n >1
5) Démontrer que
tout nombre rationnel strictement positif est égal à un terme un.
6)
Démontrer que tout nombre rationnel strictement positif est égal à un
unique terme un.
Soient a et b deux
entiers naturels non nuls.
Si un = a / b alors u2n =un+1 =a / b
+1.
u2n+1 =(a / b) / (a / b+1)= (a / b) / [(a+b) / b] = a /
(a+b).
Démonstration par récurrence que " pour tout k appartenant à N*, un
terme de un est égal à k / n".
Initialisation
: u1 = 1 est vrai.
Hérédité :
un = k /n est supposé vrai.
On note c = k /(n+1) avec k entier naturel non nul.
- Si k appartient à
[1 ; n+1[ : n+1-k appartient à [1 ; n].. La propriété est vraie.
- si k > n+1, la
division enclidienne conduit à : k = (n+1) q +r avec k entier naturel
et 0 < r < n+1.
Si r = 0 : k / (n+1)=q, donc k / (n+1) entier naturel non nul.
Si r diffère de zéro : k /(n+1) = q +r /(n+1).
Il existe n0 tel que un0 =r / (n+1).
Pour q-1 appartenant à [2 ; n0]: uq-1 =q+r /
(n+1) =k /(n+1). La propriété est vraie.
Conclusion : la propriété est vraie au rang 1 et
héréditaire, elle est donc vraie
pour tout n >1
|
...
|
....
|
Exercice 2 : Limite
sympathique !
Partie A :
Quelques exemples
1)
On considère dans cette question, pour tout entier n > 1, l’équation
x2 +x / n -1 =0 d’inconnue x.
a)
Soit n un entier naturel non nul. Démontrer que cette équation admet
une unique solution réelle positive
; on la note xn. Exprimer xn en fonction de n.
Discriminant : D
= 1 /n2 +4.
Solutions :
b) Démontrer que la suite (xn)n>1 converge ; on
note xoo sa limite.
Quand n tend vers +oo : 1 /n et 1 /n2 tendent vers zéro.
.xn tend donc vers xoo=1.
c) Démontrer que xoo est
solution de l’équation x2
−1 = 0.
Solution de cette équation x2 =1 ; x = ±1.
2) On considère dans cette
question, pour tout entier n >
1, l’équation
y2/n-y-1=0 d’inconnue y.
a)
Soit n un entier naturel non nul. Démontrer que
cette équation admet une unique solution réelle positive ; on la note yn.
Discriminant : D
=1+4/n.
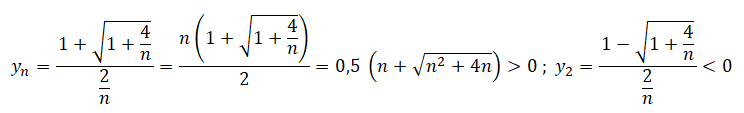
b) Démontrer que la suite (yn)n>1 diverge.
Quand n tend vers +oo, yn tend vers +oo : la suite (yn)n>1 diverge.
3) On considère dans cette question,
pour tout entier n >
1, l’équation
z3 +z2/n −1 = 0, d'inconnue z.
a) Soit n un entier
naturel non nul.
i) Étudier les
variations de la fonction z3 +z2/n −1 sur l’intervalle [0,+∞[.
Dériver : f '(z) = 3z2 +2z /n = z ( 3z +2/n).
La dérivée s'annule pour z = 0 et z = z = -2 / (3n). Cette solution est
rejetée car elle n'appartient pas à [0,+∞[.
z' >0 sur [0,+∞[ ; la fonction f(z) croît de -1 à +oo.
ii) En déduire que
cette équation admet une unique solution réelle positive ; on la note zn.
Démontrer que zn appartient à l’intervalle ] 0,1[.
Théorème de la bijection : sur [0 ; +oo[, f(z) est continue et
croissante de -1 à +oo.
0 appartient à [0 ; +oo[ ; cette
équation admet une unique solution réelle positive.
f(0) = -1 ; f(1) =1+1 /
n-1=1 / n.
-1 < 0 <1/ n.
Donc zn appartient à ]0 ; 1[
b)
Démontrer que la suite (zn)n>1 est convergente.
On pourra s’intéresser au signe du réel z3n+1
+1/n z2n+1 -1.
Quelque soit n > 1
:
z3n+1
+1/n z2n+1
-1= z3n+1 +[1 /(n+1) + 1 /(n(n+1)) ]z2n+1 -1.
Or z3n+1
+1/(n+1)z2n+1 -1 =0.
z3n+1 +1/n z2n+1 -1=1 /(n(n+1)) z2n+1 =0.
1 /(n(n+1)) =1 /n -1 /(n+1) >0.
fn(zn+1)
= z3n+1 +1/n z2n+1 -1 > 0.
Donc quelque soit n >
1 : fn(zn+1)
> fn(zn).
zn est croissante et majorée par 1, donc elle converge.
c) On note zoo la limite
de la suite (zn)n>1. Démontrer que zoo
est solution de l’équation.
z3 −1 = 0.
z3-1 =(z-1) ( z2+az+b).
Développer : z3+(a-1)z2+(b-a)z-b=0.
On identifie a =1 ; b =a = 1.
z3-1 =(z-1) (
z2+z+1).
Solution réelle z =1 =zoo.
4) On considère
dans cette question, pour tout entier n> 1, l’équation
t 3 / n−t 2 −1 = 0, d’inconnue t .
a) Soit n un entier
naturel non nul. Démontrer que cette équation admet une unique solution
réelle ; on la note tn.
g(t)=t 3-nt2
−n ; g'(t) = 3t2-2nt=t(3t-2n).
g'(t) = 0 si t =0 et si t = 2n/3.
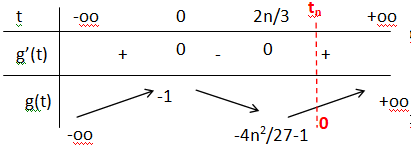
Sur [2n/3 ; +oo[, g(n) continue et croissante.Théorème de la bijection
: g(t) admet une unique solution sur [2n/3 ; +oo[.
b) La suite (tn)n>1 est-elle
convergente ? Si oui, quelle est sa limite ?
On note l la limite
réelle si elle existe.
l
appartient à [2n/3 ; +oo[.
En plus l'infini : tn
3 / n−tn 2 −1 = 0
tn 3
/ n tend vers zéro ; −tn
2 −1 tend vers −l 2 −1 =0 soit l2=-1,
impossible.
Donc l n'existe
pas, la suite ne converge pas.
Partie B : Polynômes
sympathiques
Dans les deux prochaines parties, on considère un entier d>1. La fonction P est un
polynôme de degré au plus d s’il existe des réels a0,a1,
. . . ,ad tels que :
P(x) = ad xd +ad−1xd−1 +·
· ·+a2x2 +a1x +a0 pour tout
réel x.
On dit que :
- P est initialement sympathique si a0 = −1 et si ak
> 0
pour tout entier k tel que 1 <
k < d ;
- P est faussement sympathique si a0 = −1 et si ak
< 0
pour tout entier k tel que 1 < k < d ;
- P est vraiment sympathique si a0 = −1 et s’il existe un
entier k tel que 1 <
k < d −1 et pour
lequel
a1 < 0,
a2 < 0, . . . ,ak
< 0 et ak+1 > 0, ak+2 > 0, . . . ,ad
> 0.
Enfin, on dit que P est sympathique s’il est initialement, faussement
ou vraiment sympathique.
5) Quels sont les
polynômes qui sont à la fois faussement sympathiques et initialement
sympathiques ?
Exemples : initialement sympatique : 5x2+3x-1.
Faussement sympatique : -6x3-4x-1.
Vraiment sympatique : 3x4 +4x3+2x2-x-1.
Faussement sympatique et
vraiment sympatique :
pour tout entier k tel
que 1 < k < d :
a0 = -1 ; ak > 0 et ak < 0 pour tout entier k tel que 1 < k < d : donc ak
= 0.
P(x) = -1.
6) Démontrer que tout polynôme
faussement sympathique est
a) strictement
négatif sur l’intervalle [ 0,+∞[ ;
Sur cet intervalle, xk sont positifs ou nuls et tous les coefficients ak sont négatifs.
akxk sont tous négatifs.
b) décroissant sur
l’intervalle [0,+∞[.
Dériver :
P'(x) = dad xd-1 +(d-1)ad−1xd−2 +·
· ·+2a2x +a1.
d, d-1,... sont positifs ; ad, ad-1... sont négatifs ; xd-1, xd-2... sont positifs.
P'(x) est négatif : P(x) est décroissant sur
l’intervalle [0,+∞[.
7) Soit P un
polynôme vraiment sympathique et initialement sympathique.
a) Démontrer que P
est strictement croissant sur l’intervalle [ 0,+∞[ .
a0 = −1 ;
a1 =0 ; a2=0 ; ... ak =0 ; ak+1 >0 ; ak+2 >0 ...ad >0.
P(x) = ak+1 xk+1 +ak+2xk+2 +...+adxd-1.
Dériver : P'(x) =ak+1 (k+1)xk +ak+2 (k+2)xk+1 +....+addxd-1.
ak+1 > 0 et , ak+2 ...ad >0.
xk ; xk+1 ...xd-1>0 sur [ 0,+∞[ .
P'(x) >0 : P
est strictement croissant sur l’intervalle [ 0,+∞[ .
b) Démontrer que
l’équation P(x) = 0 admet une unique solution strictement positive.
P(0) = -1 ; quand x tend vers +oo, P(x) tend vers +oo.
P(x) est strictement croissant de -1 à +oo.
P(x) est continue sur [0 ; +oo[.
Théorème de la bijection : P(x) = 0 admet une unique solution positive.
8) Soit P un
polynôme vraiment sympathique mais pas initialement sympathique.
a) Démontrer qu’il
existe un réel b > 0, un entier l > 0 et un polynôme Q
vraiment sympathique tels que
P′(x) = b xl Q(x)
pour tout réel x.
P(x) = adxd +...+ak+1xk+1 +akxk +...+a1x -1.
termes positifs. termes négatifs
Soit l+1 le plus petit entier tel que al+1 < 0.
Dériver : P'(x) = ad d xd-1 +...+(k+1)ak+1 xk + k akxk-1+...+(l+2)al+2xl+1+(l+1)al+1xl+a1.
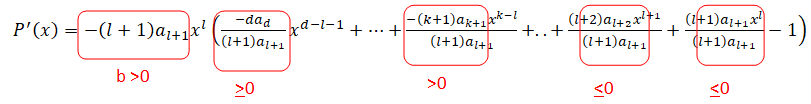
b) Démontrer qu’il
existe un réel r > 0 tel que le polynôme P vérifie les quatre
propriétés suivantes :
- P est décroissant sur l’intervalle [0, r ] ;
- P est strictement croissant sur l’intervalle [ r,+∞[ ;
- P est strictement négatif sur l’intervalle [0, r ] ;
- l’équation P(x) = 0 admet une unique solution dans l’intervalle [
r,+∞[.
P(x) = adxd +...+ar+1xr+1 +arxr +...+a1x -1.
termes positifs. termes négatifs
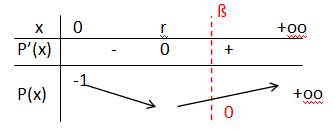
Sur (r ; +oo[, P(x) est strictement croissant d'une valeur négative à +oo.
P(x) est continue sur [0 ; +oo[.
Théorème de la bijection : P(x) = 0 admet une unique solution positive dans l’intervalle [
r,+∞[..
9) Quels sont les
polynômes sympathiques P pour lesquels l’équation P(x) = 0 admet au
moins une solution strictement positive ? Donner, dans ce cas, le
tableau de signes de P sur l’intervalle [ 0,+∞[.
|
ane.
|
|
|