Suites
récurrentes, concours général maths 2024.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Problème
1 : étude d'une suite.
Pour tout réel a > 0, on appelle suite
associée à α la
suite (un) définie par u0 = a et
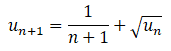
pour tout entier n >
0.
. Partie 1 : Généralités
1. Soit a
un réel positif. Démontrer que la suite (un) associée à a vérifie un > 0, pour tout entier
n > 0.
Par récurrence :
Initialisation
: u1 =1+ u0½ =1+a½
>0. La propriété est vraie au rang 1.
Hérédité :
un > 0 est supposé vrai.
1 / (n+1) > 0
et un½ >
0 ; donc par addition un+1 > 0. L'hérédité est vérifiée.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est donc vraie
pour tout n >0.
2. Soit a et ß deux réels tels que 0< a < ß. On note (un)
la suite associée à a
et (vn) la suite
associée à ß.
Démontrer que un <
vn, pour tout entier n > 0.
Par récurrence :
Initialisation
: u0 = a et v0 = ß ; 0< a
< ß donc u0 < v0. La
propriété est vraie au rang zéro.
Hérédité :
un < vn, est supposée vraie.
un+1 =
1 / (
n +1)
+ un½ ; vn+1 =
1 / (
n +1)
+ vn½ ; un+1
- vn+1 = un½ - vn½ < 0.
un+1 < vn+1 . L'hérédité est vérifiée.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est donc vraie
pour tout n >0.
3.
On note (wn) la suite associée à 0. Démontrer que wn
> 1,
pour tout entier n >
1.
Initialisation : w0=0 ; w1 = 1+0½
=1. La propriété est vraie au rang 1
Hérédité
: wn > 1,
est supposée vraie.
wn+1 = 1 / (n+1)+wn½
.
Or wn½ > 1 et 1 / (n+1) > 0, donc wn+1 > 1. L'hérédité est vérifiée.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est donc vraie
pour tout n >1
.
4. Soit a un réel positif ou nul. On
suppose que la suite (un) associée à a converge vers un réel l.
Déterminer la valeur de l.
En plus l'infini
: un= l.
un+1 =
1 / (
n +1)
+ l½
. Or 1/(n+1) tend vers zéro si n tend vers plus l'infini : un+1 = l½ .
Il faut résoudre : l
= l½
.
Solutions : l = 0 ou
bien l = 1.
Or wn >
1, donc l = 1.
5. Soit a un réel tel que a >
(3+ 5½) /
2
.
Justifier que la suite associée à a est strictement
décroissante.
Que peut-on en déduire en terme de convergence ?
Par
récurrence :
Initialisation : u0 = a et u1 =1+ u0½ =1+a½ ; u1 -u0 =1+a½
-a.
On pose x =a½ . Etude du
signe de f(x) = -x2+x+1 sur R+.
-x2+x+1=
0 ; discriminant : 12+4=5.
Racines : x1 =(-1+5½) / (-2)=(1-5½)/ 2
et x2 = (-1-5½) / (-2)=(1+5½)/ 2.
f(x) < 0 si x appartient à ](1+5½)/
2. ; +oo[.
Donc u1 < u0. La propriété est vraie au rang 1.
Hérédité :
un+1 < un est supposé vrai.
un+2=1 / (
n +2)
+ un+1½ .
0 < un+1
< un
donc un+1½
< un
½.
1 / (
n +2)
+ un+1½ < 1 / (
n +2)
+ un½ .
1/(n+2) < 1 /(n+1) et un+1½ < un ½.
Par suite un+2 < un+1.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est donc vraie
pour tout n >1
Pour tout n entier
naturel un >
0.
Pour tout a >
(3+5½) / 2 la suite (un) est décroissante. Donc (un)
converge si a
> (3+5½) / 2.
|
...
|
....
|
Partie 2 :
Dans toute cette partie,
on note (tn) la suite associée à 4 et on définit la suite (sn)
par
sn = n(tn −1), pour tout entier n > 0.
6. Démontrer, pour
tout entier n > 1
, l’encadrement :
1+
2
/ n < tn
< 1+
3
/ n
.
Initialisation
: t0 = 4 ; t1 =1+4½ = 3 ; 1+
2
/ 1 < t1
< 1+
3
/ 1 soit 3 < t1 < 4.
La propriété est vraie au rang 1.
Hérédité : 1+
2
/ n < tn < 1+
3
/ n
est supposé vrai.
Quelque soit n entier tel que n > 1: tn½
<
(1+3/n)½.
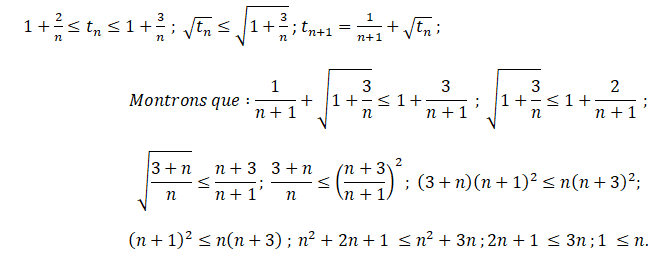
L'hérédité est vérifiée.
Conclusion
: la propriété est vraie au rang 1 et héréditaire, elle est donc vraie
pour tout n >1
7. Démontrer, pour tout entier n > 1, l’encadrement :
2 < sn < 2+
6
/ n
.
tn+1=1/(n+1)+tn½.
sn= n(tn-1).
Or 1+
2
/ n < tn
< 1+
3
/ n
.
Soit : 2 / n < tn -1 <
3
/ n
.
2 <
sn <
3 .
Par récurrence on montre que sn < 2+
6
/ n
.
Initialisation : t0 =4 ; s0 =0(4-1)=0.
t1=1+4½ = 3 ; s1=1(3-1)=2 < 2+
6
/ 1
.
La propriété est vraie au rang 1.
Hérédité : sn < 2+
6
/ n est supposée vraie.
sn+1 = (n+1)(tn+1 −1)
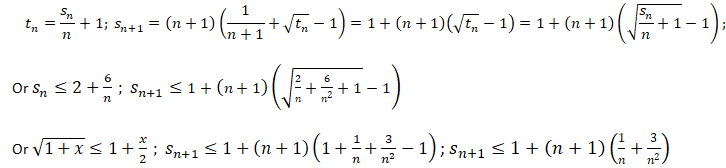
Pour n = 1 : s2 =9 ; 2+6 /n = 8.
Pour n = 2 : s3 =19 / 4 ; 2+6 /n = 5.
Si n > 2 : sn < 2+
6
/ n
.
8. Déterminer la
limite suivante
quand n tend vers +oo.
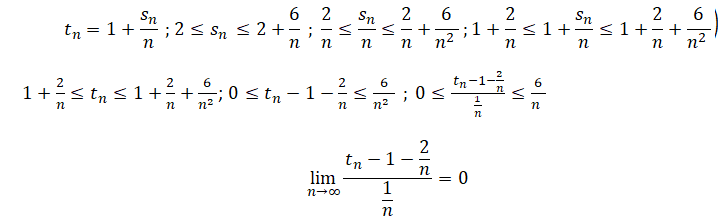
|
ane.
|
|
|