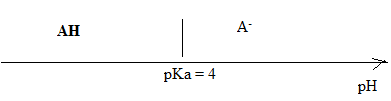Mathématiques,
Chimie, biologie.
Concours technicien police technique et scientifique 2024
(Paris).
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Biologie
1. La drépanocytose:
a) est une maladie infectieuse causée par un parasite.
b) confère un avantage sélectif dans les zones impaludées. Vrai.
c) est plus fréquente dans les régions où le paludisme est rare.
d) augmente la probabilité de développer une forme grave de paludisme. Faux.
2. L'hémoglobine:
a) est une enzyme impliquée dans la digestion des protéines
b) est un acide aminé composé de quatre sous-unités identiques codées par un seul gène
c) est une molécule constituée d'un noyau d'hème et de quatre chaînes polypeptidiques. Vrai.
d) est une protéine présente dans les globules rouges et responsable de la fixation du fer.
3. Dans l'arbre généalogique de la famille décrite, le mode de transmission de la drépanocytose semble être :
a) Autosomique récessif. Vrai.
b) Autosomique dominant
c) Lié au chromosome X.
d) Lié au chromosome Y.
:
4. Les individus atteints de drépanocytose :
a) ont un génotype homozygote pour la forme normale du gène de l'hémoglobine.
b) ont un génotype hétérozygote pour la forme mutante du gène de I'hémoglobine
c) ont un génotype homozygote pour la forme mutante du gène de I'hémoglobine. Vrai.
d) ont un génotype hétérozygote pour la forme normale et la forme mutante du gène de I'hémoglobine.
5. Le risque qu'un enfant issu du couple ll-3 et ll-4 soit atteint de drépanocytose est de:
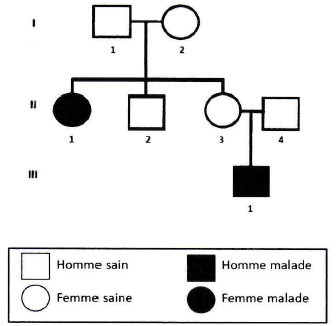
a) 0 % ; b) 25% vrai ; c) 50% ; d) 75%.
6. Le risque qu'un enfant issu du couple ll-3 et ll-4 soit porteur sain de la drépanocytose est de:
a) 0 % ; b) 25% ; c) 50% vrai ; d) 75%.
L' EPO (érythroporétine) est une principalement synthétisée au
niveau des reins, mais qui peut aussi être synthétisée par voie
chimique. Elle stimule la production de globules rouges ,et donc la capacité à transporter l'oxygène jusqu'aux muscles.
Chimie:
1. Donnez la
définition d'un acide selon Brônsted.
Un acide est une espèce susceptible de céder un proton H+.
2. Quelle est la caractéristique
d'une solulion tampon ?
a) C'est une
solution dont le pH augmente fortement par l'ajout d'une base forte.
Faux.
b) C'est une
solution dont le pH diminue fortement par l'ajout d'ul acide fort. Faux.
c) C'est une
solution dont le pH varie légèrement lors de l'addition modérée d'un
acide fort ou d'une base forte. Vrai.
3.Tracez le diagramme de prédominance d'un couple acide/base
tAHl/tA-l dont le pKa est 4.
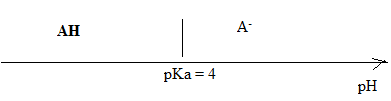
2. ApH = 3, quelle
est la relation entre la concentration de la forme acide et la
concentration de la forme basique.
a) [AH] est 10 fois inférieure à [A- ]
b) [AH] est 10 fois supérieure à [A- ]. Vrai.
c) [AH] = [A-]
d) [AH] est 100 fois inférieure à [A-].
pH = pKa + log ([A- / [AH]).
3 = 4 + log ([A- / [AH]) ; -1 = log ([A- / [AH]) ; [A- ] / [AH] = 10-1 =
0,1 ; [AH] = 10 [A- ] .
4. On effectue le
titrage d'une solution d'acide chlor§drique qui contient l'acide H3O+
par une solution de soude qui contient la base HO-.
La courbe du titrage obtenue est la suivante :
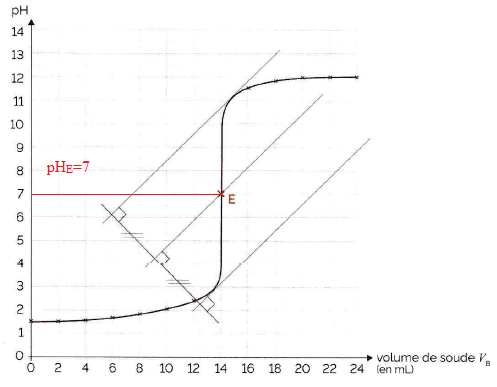
On souhaite trouver un indicateur coloré qui permettra de détecter
visuellement l'équivalence.
La zone de virage de l'indicateur coloré doit contenir le pH du point
équivalent : bleu de bromothymol.
5. Du jus de pomme
au vinaigre
Le vinaigre de cidre est obtenu par double fermentation de jus de
pomme, la fermentation alcoolique et acétique.
La fermentation alcoolique est due à I'oxydation du glucose contenu
dans le jus de pomme en présence de levures. Il se forme de l'éthanol
et du dioxyde de carbone. On obtient du cidre. La principale
transformation du cidre en vinaigre est due à des microorganismes,
Mycoderma acetii, qui fixent les molécules de dioxygène sur l'éthanol,
ce qui conduit à Ia formation d'acide acétique. Cette
transformation est appelée fermentation acétique.
Fermentation alcoolique
Le glucose linéaire se trouve sous deux formes énantiomères, le
D-Glucose et le L-Glucose. Lors de la fermentation alcoolique, seul le
D-glucose majoritairement présent dans la nature se transforme sous
l'effet de Ia zymase, une enzyme produite par des levures. La
représentation de Cram de la molécule de D-glucose est donnée
ci-dessous :
1. Établissez
l'équation de la réaction de fermentation alcoolique du D-glucose.
Pourquoi cette fermentation est elle qualifiée de fermentation
alcoolique ?
C6H12O6 --->
2C2H6O
+ 2CO2(g)
La fermentation
est qualifiée d'alcoolique car l'un des produits est un alcool.
Réponse a.
2. Quel est le rôle
de la zymase dans la fermentation alcoolique ?
a) Accélérer la réaction. Vrai.
Un catalyseur accélère la réaction.
b) Augmenter le rendement
c) C'est un réactif
d) C'est un produit.
Fermentatîon acétique.
3. Quel est le nom
en nomenclature systématique de l'acide acétique :
a) acide éthanoïque. Vrai.
b) acide méthanoïque
c) acide carboxylique
d) acide chlorhydrique
4. Quelle est
l'écriture correcte de la réaction de fermentation acétique due aux
Mycoderma acetii ?
a) 2C2H6O+ O2 -->2C2H4O2+H2.
b) C2H6O+
O2 -->C2H4O2+H2O.
Vrai.
5. Par
déduction, quels sont les couples oxydant/réducteur mis en jeu dans la
réaction. Indiquez la bonne réponse.
C2H4O2 / C2H6O et O2 / H2O.
Oxydation du réducteur C2H6O
par l'oxydant O2. Réponse c.
Analyse d'un cidre en
cours de fermentation.
La teneur acétique d'un vinaigre, exprimé en degré acétimétrique est
égale à son acidité totale mesurée à 20°C et exprimée en grammes
d'acide acétique pour 100 mL de vinaigre. La teneur acétique minimale
des vinaigres est de 5,0 g d'acide acétique pour 100 mL de vinaigre.
Un échantillon de cidre mis à fermenter est prélevé pour vérifier sa
teneur en acide acétique. Un volume prélevé V = 25 mL de
I'échantillon dilué 10 fois est titré par une solution d'hydroxyde de
sodium de concentration molaire c = 0,2 mol.L-1.
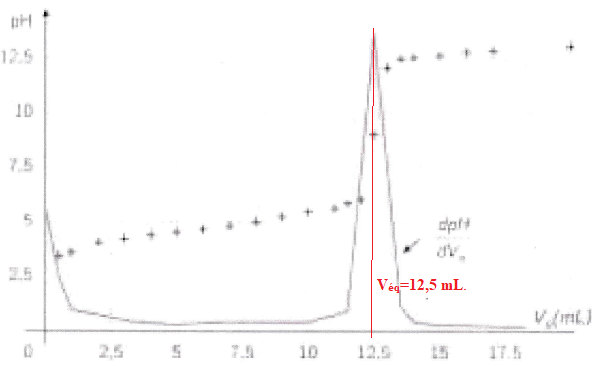
Le suivi pH-métrique du titrage du cidre au cours de sa fermentation
conduit au graphe représenté ci-dessous et donnant l'évolution du pH du
milieu réactionnel et de sa dérivée en fonction du volume Vb
de solution d'hydroxyde de sodium versé.
On définit deux quantités de matière :
ncidre = quantité de matière d'acide acétique dans le cidre avant le titrage .
nsoude : quantité de matière d'ions OH-
versée à l'équivalence .
6. Quelle relation
peut s'écrire entre ces deux grandeurs :
ncidre
dilué =nsoude.
7. Quelle est
l'expression de la quantité de matière de soude versée à l'équivalence
en fonction des données de l'énoncé
nsoude= c Véq ; réponse
d.
8. Quelle est
I'expression du degré d'acidité d du cidre sachant que la masse m
d'acide acétique dans l'échantillon de solution dix fois diluée de
volume V ?
ncidre dilué =nsoude : cdilué V = c Véq
;
cvinaigre = 10 c Véq / V
mol dans un litre de cidre.
Soit c Véq
/ V mol d'acide acétique dans 0,1L = 100 mL de vinaigre.
Masse d'acide acétique : m = M acide acétique c Véq / V.
d = M acide acétique c Véq / V.
9. D'après la
courbe de pH-métrie, quelle est la valeur du volume de soude versé à
I'équivalence ?
12,5 mL. Réponse b.
10. Quel est alors
le degré d'acidité de ce cidre ?
d = 60 x 0,2 x 12,5 / 25= 6. Réponse c.
d
> 5, ce cidre peut être commercialisé sous le nom de vinaigre.
Exercice 6 :1point
Une solution de GBL (gamma-butyrolactone) est dosée à c =1,017 mg / mL.
La densité du GBL est de 1,130 g /cm 3.
1. En fonction de
la concentration mesurée et de la densité, exprimez la formule du
calcul du pourcentage de pureté.
1,017 mg de GBL dans 1 mL de solution.
1,017 mg de GBL
( 1,017 10-3 g ) dans 1,13 g de solution.
Pourcentage de pureté = 1,017 10-3 / 1,13 x100 = 0,9 % (
environ 1 %). Réponse d.
Exercice 7: 2points
En France, il est interdit de conduire avec une alcoolémie supérieure à
0,5 g d'alcool par litre de sang (ou 0,25 mg d'alcool par litre d'air
expiré). L'alcoolémie est le taux d'alcool présent dans le sang. Elle
se mesure en grammes par litre de sang (analyse de sang) ou en
milligrammes par litres d'air expiré (éthylotest, éthylomètre).
1. Quelle est la
réaction d'oxydoréduction que I'on peut observer entre l'éthanol et les
ions Cr2O72- (ions bichromates)?
3 fois{ C2 H6
O +H2O=
C2H4 O2 + 4
électrons + 4H+}.
2 fois{Cr2O72- + 6
electrons +14 H+
= 2 Cr3+ + 7 H2O}.
3 C2 H6 O + 2Cr2O72-
+28 H+ +3H2O---> 3 C2H4 O2 + 4 Cr3+
+ 12 H+ + 14 H2O.
3 C2 H6 O + 2Cr2O72-
+16 H+ ---> 3 C2H4 O2 + 4 Cr3+ + 11 H2O.
2. Un
éthylotest est composé de cristaux de gel de silice (blancs au départ)
imprégnés de bichromate de potassium (jaune orangée) à la fin de
détecter la présence d'alcool dans I'air expiré par un conducteur. Le
conducteur doit remplir avec son souffle un ballon de 1 L et le vider
dans le tube qui contient ces cristaux.
Quel indicateur permet à l'agent de police de savoir que Ie test est
positif à la présence d'éthanol ?
Les cristaux deviennent vert, couleur due aux ions Cr3+. Réponse c.
On souhaite préparer un mélange de plusieurs composés cannabinoïdes
dans du méthanol dans une fiole de 10 mL, et dont la
concentration finale sera de 50 µg/mL.
Composé 1 :THC (delta-9-tétrahydrocannabinol) ; 10 mL à 1 mg / mL.
Composé 2 : l1-OH-THC (11-hydroxy-delta-9-tHC) : 10 mL à 1 mg / mL.
Composé 3 :THC-COOH (11-Nor-9-carboxy-THC) : 10 mL à 10 mg / mL.
1. Quel volume de
chaque composé faudra t-il introduire dans la fiole ?
500 µg dans 10 mL ou 0,5 mg dans 10 mL.
Par exemple : 2 mL du composé 1 +2 mL du composé 2 +0,1 mL du composé 3.
2. La fiole est
ensuite complétée par du méthanol. Quelle situation correspond à la
bonne utilisation de la fiole jaugée ?
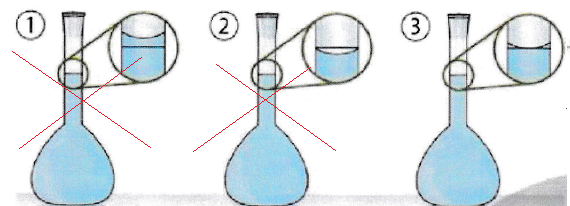
Exercice 9: 1point
Énoncez la loi de Beer-Lambert et définissez chaque terme avec leurs
unités.
A= log (I0/I) = elc ( A est l' absorbance ou densité optique)
où e est un coefficient caractéristique de la
substance appelé coefficient d'absorbance (L
mol-1 cm-1), l est l'épaisseur de la cuve (cm) et c la
concentration de la solution (mol/L).
|
...
|
....
|
Mathématiques
1. 2,5 points
Simplifiez les expressions suivantes :
A = e3 x e4 = e3+4 = e7.
B = e-5 / e2 = e-5 x e-2 = e-7.
C = e5x+7 * e-x-3 / e2x+3
=exp(5x+7-x-3-2x-3) = exp(2x+1).
D= 1 / e-1 = e.
E=e2*e-4 = e2-4 = e-2.
2. 1,5 points.
Pour chaque fonction donnez le domaine sur lequel elle est dérivable et
sa dérivée :
a. f(x) = (2x2+3x-3)4.
Dérivable sur R.
On pose u = 2x2+3x-4 ; u'= 4x+3 ; f(u ) = u4 ; f
'(u) = 4u' u3.
f(x) = 4 (4x+3) (2x2+3x-3)3.
b. f(x) = xn
avec n entier relatif différent de 0 et de 1.
f '(x) = n xn-1.
c. g(x) = (x+1) ex.
On pose u = x+1 et v = ex ; u' = 1 ; v' = ex.
u' v + v' u = ex +(x+1)ex = (x+2)ex.
3. lndiquez la
bonne réponse :
1.La dérivée de la
fonction / définie par f (x) = 3* x½+ x +1 est :
f '(x) = 3 *½ x-½+1. Réponse c.
2. La dérivée de la
fonction f définie par / (x) = 3x2 - 5 x+ 1 est :
f '(x) = 6 x-5. Réponse b.
3. La dérivée de la
fonction / définie par / (x) = 3x5-5x3+2x+1 est :
f '(x) = 15 x4 -15x2 +2. Réponse a.
4. La dérivée de la
fonction f définie par / (x) = 3 /(2x+1) est :
f(x) = 3 (2x+1)-1 ; f '(x) = 3 *(-1)* 2*(2x+1)-2
= -6 (2x+1)-2 . Réponse c.
4. 3 points..
On considère deux variables statistiques x el y observées sur une même
population de n individus.
on note x1, x2, ..., xn les valeurs
relevées pour la variable x et y1,ÿ2, ..., yn
les valeurs relevées pour la variable y.
1. Exprimez la
série statistique à deux variables associées à ces valeurs.
(x1 , y1) ; (x2 , y2) ...(xn,
yn).
2. Donnez la
définition du nuage de point correspondant.
L'ensemble des points Mi de coordonnées (xi, yi)
avec 1 < i < n est appelé nuage de
points associé à cette série.
3. Donnez la
définition du point moyen correspondant
Le point moyen a pour coordonnées les moyennes respectives des xi
et des yi.
5: 7 points
Adrien va participer à une compétition culinaire organisée par sa
ville, sur le thème des macarons. ll souhaite donc s'entraîner tous les
jours pour maîtriser sa recette.
Quand il essaie le premier jour, la probabilité qu'il réussisse ses
macarons est de 0,3. Par la suite, il a remarqué que :
- si un jour donné, il réussit ses macarons, la probabilité qu'il les
réussisse le jour suivant est de 0,9
- si un jour donné il ne réussit pas ses macarons, la probabilité qu'il
ne les réussisse pas le jour suivant est de 0,7
On note Ei l'événement « Adrien a réussi ses macarons le i
ème jour ».
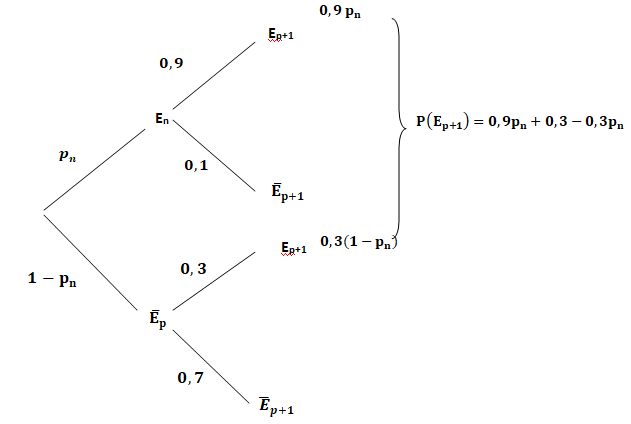
1. On donne l'arbre
pondéré correspondant à cette situation.
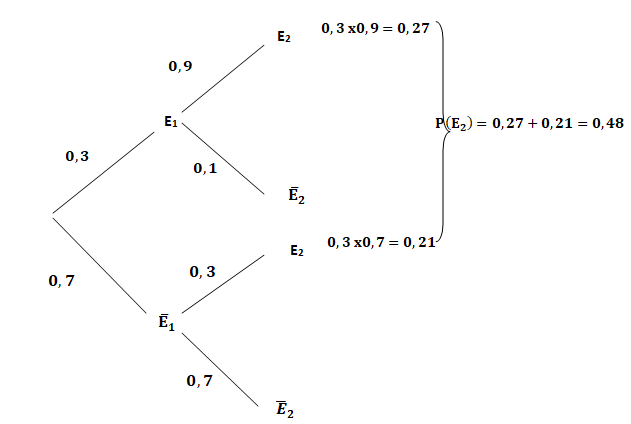
2. On généralise
en notant, pour tout entier naturel non nul n, En
l'événement " Adrien a réussi ses macarons le
n-ième jour " et pn la probabilité associée à E.
a) Montrez que pour
tout entier naturel non nul n, pn+1=0,6pn+0,3.
b) Pour tout entier
naturel nonnul n,onconsidère la suite (un) définie par un=pn-0,75:
Montrez que (un) est une suite géométrique, dont vous
donnerez la raison et le premier terme u1
un+1=pn+1-0,75 =0,6 pn+0,3-0,75=
0,6 pn-0,45 = 0,6(pn-0,75)= 0,6 un.
Raison q = 0,6 ; u1 = p1-0,75 =0,3-0,75 = -0,45.
c) Pour tout entier
naturel non nul n, donnez l'expression de un en fonction de
n. En déduire pn en fonction de n.
un = -0,45 x0,6n.
pn = un+0,75=0,75 --0,45 x0,6n.
Dans chaque cas suivant, indiquez sur votre copie si l'affirmation est
vraie ou fausse en justifiant par un calcul le cas échéant :
1) g est la
fonction définie sur l par g(x)= exp(x) *exp[(-x+1)2 ]/
(exp(-x+4).
Affirmation
: la fonction g est constante sur R. Faux.
g(x) = exp[(x +(-x+1)2 -(-x+4)] =exp[2x-4+x2+1-2x]=exp(x2-3).
2) un
est la suite définie pour tout entier naturel par un= 5
exp(0,1 n-1).
Affirmation
: la suite un est géométrique de raison e0,1 et
de premier terme u0 =5 /e. Vrai.
u0=5 / e ; u1 =5 exp(-0,9)=5 / e exp(-0,9 +1)= 5
/e exp(0,1) = u0 exp(0,1).
u2 =5 exp(-0,8)=5 / e exp(-0,8 +1)= 5 /e exp(0,2) = u0
[exp(0,1)]2.
3) Affirmation : e-1000
est égal à 0. Faux.
5,076 x10-435.
4) Dans ce repère,
la courbe peut représenter la fonction définie sur R par :

a) . Quand x tend vers -oo, f(x) tend vers + oo.
c)et d) f(0) =2 alors que sur le graphe on lit f(0) = 1.
|
|