Mouvement
d'une cabine de téléphérique, statique des fluides, lentille
convergente, concours TSEEAC 2024 .
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
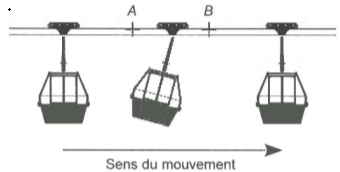
Premiere phase : déplacement lent à vitesse constante. La cabine
parcourt d1=1,0 m en t1=5,0 s.
Seconde phase entre A et B : la vitesse augmente progressivement ; la
tige reste immobile inclinée d'un angle a compris entre 0 et 10° par
rapport à la verticale. La distance AB =dAB= 2,0 m est
parcourue en tAB=2,0 s.
Troisième phase à partir de B : la vitesse redevient constante. La
cabine parcourt d2=4,0 m en t2=2,0 s.
Masse de la cabine m = 3 tonnes.
Question 16.
Lors de la
seconde phase, la force totale qui s'applique à la cabine a la
direction et le sens suivant :
La cabine est soumise à son poids, verticale, vers le bas, valeur mg et
à la tension du câble. La vitesse croît, l'accélération a le sens du
mouvement.
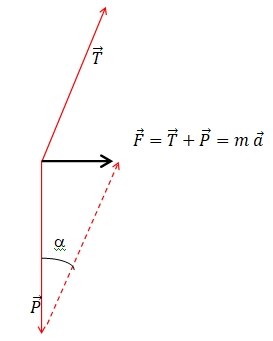 Réponse A Réponse A
Question 17.
Dans une série d'expérience avec un dynamomètre pour m = 100 g, L =
30,0 cm et a = 10°, quelle est la résultante des forces F ?
F = P tan a =0,1
x 9,8 x tan 10 ~0,17 N. Réponse B
Question 18. Dans le
cas de la cabine la résultante des forces vaut :
P = mg = 3 103 x 9,8 =2,94 104 N.
F = 2,94 104 x tan 10 ~5,2 103 N.
Question 19.
Après le
point B, quelle est la vitesse de la cabine ?
La cabine parcourt 4,0 m en 2,0 s.
v = 4,0 / 2,0 = 2,0 m/s. Réponse A
.
Question 20. Quelle alors son énergie
cinétique ?
½mv2 =0,5 x3 103 x22 =6,0 103
J = 6,0 kJ. Réponse B
Question 21 . Entre A et B, l'expression de la force F supposée constante
est :
La variation de l'énergie cinétique entre A et b est égale au travail
de la résulante des forces F.
½mvB2 -½mvA2 = F dAB
;
vB = d2
/ t2 ; vA = d1 /t1 ;
F =½m ( d22
/ t22 -d21
/ t21) / dAB.
F =½m ( d22
t21 -d21
t22) / ( t21t22dAB). Réponse B
Question 22. Entre A
et B, la valeur de F est :
F =1500 (42 x 52-12 x 22) /(52 x22
x2 )~ 3 103 N ou 3 kN. Réponse D
Question 23. Lors de la seconde
phase, quelle est la valeur de l'angle a ?
F = P tan a ; tan a = F / P =3 103 / (3 103
x9,8) ~0,10 ; a
~5,8 °. Réponse C
Question 24..Lors de la seconde phase, quelle est l'expression de tAB
?
F = m a = ½m ( d22
t21 -d21
t22) / ( t21t22dAB).
a = ½ ( d22
t21 -d21
t22) / ( t21t22dAB).
Vitesse entre A et B, primitive de l'accélération : v = a t + Cste = a
t + vA.
vB = a tAB +vA.
tAB = (vB-vA) / a = (d2 / t2
-d1 / t1
) / a =(d2 t1 -d1 t2 ) / (a t1 t2)
a= F / m .
tAB =m(d2 t1 - d1 t2 ) / (F t1 t2). Réponse A
|
...
|
....
|
Air
sous faible pression.
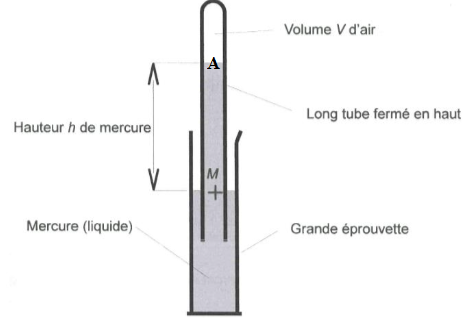
Surface au niveau de la séparation entre le mercure et l'air dans le
tube : S =2,0 10-5 m2.
Pression en M = pression atmosphérique = Patm = 1,01 105
Pa.
Masse volumique du mercure : µ = 13,6 kg / L = 13 600 kg m-3.
Pour h = 0, le volume d'air est V0 = 1,00 mL.
Question 25.
Pour h = 10,0 cm la pression P du volume d'air vaut :
PM-PA = µg h.
PA = PM-µg h= 1,01 105 - 13 600 x9,81
x0,10=8,76 104 Pa. Réponse B
Question 26.
Dans ces conditions, quelle est l'expression de V ?
La température étant constante et l'air se comportant comme un gaz
parfait :
P0V0 = PA V.
PM-PA = µg h.
V = P0V0 / PA = P0V0
/ (PM - µg h) = P0V0 / (Patm
- µg h). Réponse C
Question 27.
Quelle est l'intensité de la force exercée par l'air sur le mercure si
h = 10 cm ?
F S= PA.
PA=8,76 104 Pa ; F = 8,76 104 x
2,0 10-5 ~1,8 N. Réponse A
Lentille convergente.
Question 28.
On place un objet AB à 30 cm d'une lentille convergente. L'image réelle
A'B' se trouve à 90,0 cm de AB. Quelle est la distance focale f de la
lentille ?
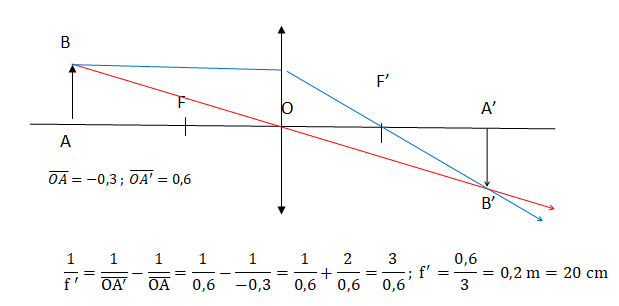 Réponse B. Réponse B.
Question 29.
Pour former à l'aide de cette lentille une image réelle inversée par rapport à l'objet
Cette lentille donne une image trois fois plus petite d'un objet réel. Quelle doit être la distance objet-lentille ?
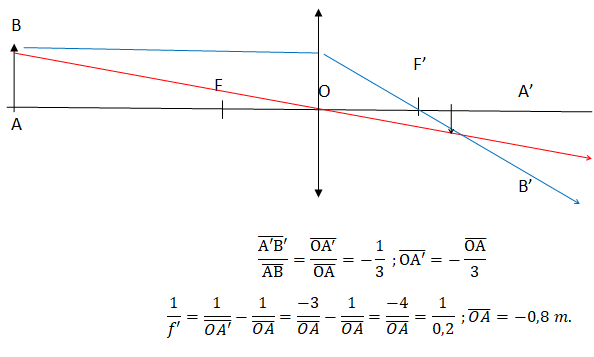 Réponse D. Réponse D.
Question 30.
Cette lentille donne une image virtuelle d'un objet réel. La distance
entre l'objet et la lentille doit être choisie parmi les valeurs
suivantes.
7 cm ; 13 cm ; 27 cm ; 33 cm.
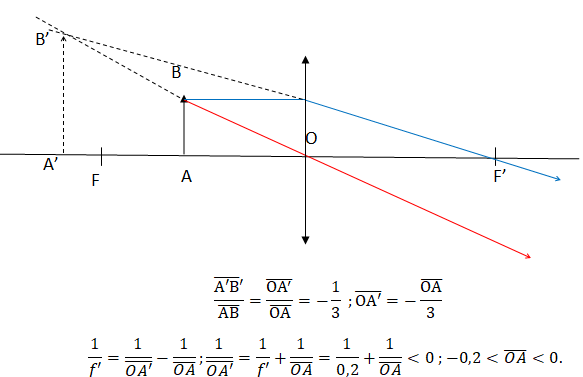
|
ane.
|
|
|

 Réponse
Réponse 
 Réponse
Réponse  Réponse
Réponse 