Aurélie septembre 04

Iceberg ; interactions de gravitation et électrique

le voilier peut-il se retourner ? pendule électrique ; plan incliné avec frottement

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


Iceberg

Les icebergs sont constitués de glace, dont la masse volumique est égale à rglace=900 kg.m-3. Soit V le volume d un iceberg et Vi son volume immergé dans l'eau. La masse volumique de l'eau est égale à r eau= 1000 kg.m-3. Calculer le rapport Vi/V. On néglige la poussée d'Archimède qui s'exerce sur la partie émergée de l'iceberg .

corrigé
L'iceberg est un solide en équilibre soumis à 2 forces, son poids et la pousée d'Archiméde.

Ces deux forces sont donc opposées, de même droite d'action, sont de sens contraire et ont même valeur.

Exprimons le poids de l'iceberg : P=mg avec m= masse volumique de la glace * Volume total de l'iceberg

P=rglace V g.

La poussée d'archiméde est égale au poids d'eau déplacé soit P= r eauVi g

Comme l'iceberg est en équilibre puisqu'il flotte, P= P soit rglace V g = r eauVi g

on simplifie g : rglace V = r eauVi

Vi/V=rglace/r eau = 900/1000 = 0,9.


Interactions

 

  1. Deux objets ponctuels, de masses égales m= 1 mg , portent des charges identiques q. La résultante des forces électrostatique et gravitationnelle agissant sur chaque objet est nulle.
    - Représenter sur un schéma les deux objets et les forces d'intéractions.
    - Donner l'expression des forces agissant sur un objet,. En déduire la valeur de la charge q.
  2. Quelles charges électriques positives et égales faudrait-il disposer sur la Terre et la Lune pour que les forces électriques aient même valeur que les forces de gravitation ?
    - A quelle quantité de charges élémentaires cela correspondrait-il ?
    Données : masse de la Terre, Mt = 6,0 1024 kg ; masse de la Lune, Ml = 7,4 1022 kg ;
    distance Terre-Lune D = 3,84 108 m
  3. La distance entre les centre de deux objets sphériques identiques est égale à D=0,20 m. Ils portent une charge q et ont une masse m, répartie de façon sphérique. En prenant q=10 C, calculer la valeur de m pour que les interactions entre les deux objets se compensent. Commenter le résultat.
corrigé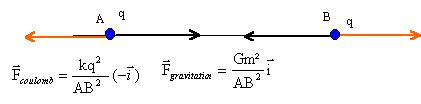

i est un vecteur unitaire de l'axe AB.

Les forces de gravitation et de coulomb sont opposées et ont même valeur.

k q²/AB² = G m²/AB² soit k q² =G m² ; q² = Gm²/k

q= m ( G/k)½.

m = 10-6 kg ; k= 9 109 ; G= 6,67 10-11 S.I.

q= 10-6 ( 6,67 10-11 / 9 109 )½ = 8,6 10-17 C.

valeur de la force de gravitation : F1 = G.Mt.Ml/D² avec G= 6,67 10-11 S.I., la constante de gravitation.

valeur de la force électrostatique : F2= 9.109.Q²/D²

F1=F2 donne : G.Mt.Ml/D² = 9.109.Q²/D²

G.Mt.Ml = 9.109.Q²

Q² = G.Mt.Ml / 9.109.

Q= racine carrée (6,67 10-11*6 1024*7,4 1022/ 9.109)

Q = 5,737.1013 C

Une charge élémentaire = 1,602 10-19 C

5,737.1013 C correspond à 5,737.1013/1,602 10-19 = 3,58.1032 charges élémentaires.

valeur de la force de gravitation : F1 = G.m²/D² avec G= 6,67 10-11 S.I., la constante de gravitation.

valeur de la force électrostatique : F2= 9.109.q²/D²

F1=F2 donne : G.m²/D² = 9.109.q²/D²

G.m² = 9.109.q²

q² = G.m² / 9.109.

m = q *racine carrée (9.109/6,67 10-11 )

m= 10*1,16 1010 = 1,16 1011 kg , valeur très grande.

 

Le voilier peut-il se retourner ?

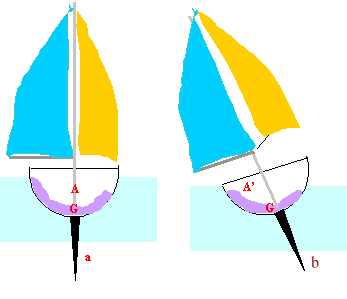
Afin de renforcer la sécurité des voiliers et faciliter leur retournement après un chavirage, le règlement des courses exige la présence sur chaque voilier de deux des dispositifs suivants : quille mobile; ballon d'air, ballast d'eau.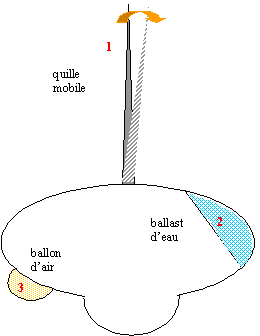

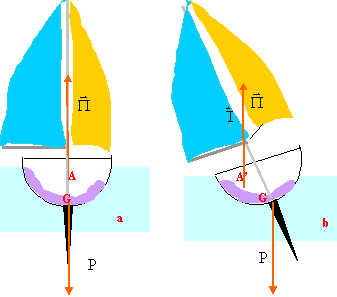
  1. Le bateau est à flot, immobile sur une mer calme, en absence de vent ( a) . Quelles sont les deux principales forces qui agissent sur le bateau ?
    - Les représenter en précisant l'échelle . Masse du bateau m = 5,8 t ; g= 10 N/kg
    - Calculer le volume de la partie immergée du bateau si la masse volumique de l'eau de mer vaut r= 1030 kgm-3.
  2. Le bateau gîte. La position du centre de gravité G n'est pas modifiée tandis que le point d'application de l'autre force est A'. Justifier le déplacement de A en A'.
    - Représenter les forces agissant sur le bateau ( schéma b).
    - Quel est l'effet de l'ensemble de ces deux forces ?
    - Que se passeraît-il si le point G était trop haut ?
  3. Le bateau est retourné. Représenter les deux forces définies question 1.
    - Quel force supplémentaire le ballon d'air permet-il d'exercer sur le bateau ? Quel est son intérêt ?
  4. Quel intérêt présente la possibilité d'incliner la quille lorsque le bateau est retourné ?
corrigé
Le bateau est à flot, immobile sur une mer calme, en absence de vent : le bateau est soumis à son poids appliqué au centre de gravité G et à la poussée d'Archimède appliquée au centre de poussée A ( centre géométrique du volume d'eau déplacé).

Ces deux forces ont même valeur, ont même ligne d'action, la verticale, et sont de sens contraire.

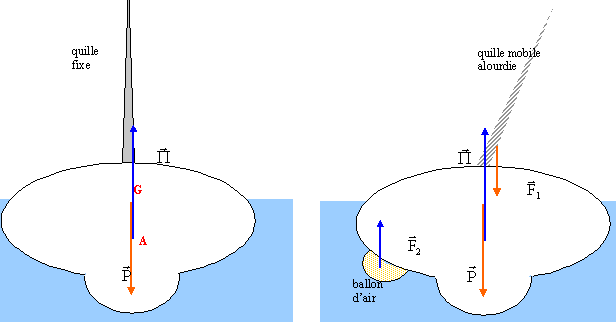
poids : mg = 5800*10 = 58 000 N ( échelle : 1 cm pour 10 000 N par exemple )

poussée = poids du volume V (m3) d'eau de mer déplacé)

P= Vr g = 58 000 soit V= 58000/(r g)= 58000/(1030*10)= 5,6 m3.

Le bateau gîte. La position du centre de gravité G n'est pas modifiée tandis que le point d'application de l'autre force est A'.

Le point d'application de la poussée est le centre géomètrique du volume d'eau déplacé : si le bateau gite, le point A, centre de poussée est déplacé du côté où le bateau gite.

Si A' est au dessus de G, les deux forces constituent un couple dont l'effet est la rotation : cette rotation tend à ramener le bateau dans la position du schéma a.

Par contre si G est trop élevé, situé au dessus de A', l'effet du couple est de faire chavirer, retourner, le bateau. Pour abaisser G on diminue la masse du mat et on alourdit la quille de plusieurs centaines de kg.

Les deux forces F1 et F2 constituent un couple dont l'effet est la rotation : cette rotation tend à ramener le bateau dans la position du schéma a.

Un solide S de poids P=10 N est posé sur une table inclinée d'un angle de 30° sur l'horizontale. Le contact entre le solide et le table est supposé sans frottements. Le solide est maintenu en équilibre sur la table grace à un ressort dont l'axe est parrallèlle a la table et de raideur k= 200N/m. Calculer l'allongement de ce ressort et determiner la valeur de la réaction de la table sur le solide S.

corrigé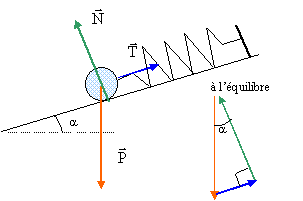

La bille est en équilibre sous l'action du poids, de l'action du support et de la tension du ressort.

Dans le triangle dessiné : cos a = N/P soit N= P cos a = 10 cos 30 =8,7 N.

sin a = T/P soit T= P sin a = 10 sin 30 = 5 N

Or la tension du ressort est proportionnelle à son allongement (l-l0) : T= k(l-l0)

soit (l-l0)= T/k = 5 / 200 =0,025 m = 2,5 cm.


Une bille en acier de masse m est suspendue au bout d'un fil de masse négligeable. On approche d'elle un aimant placé horizontalement. Le fil s'incline d'un angle a par rapport à la verticale. Déterminer les caractéristiques (direction sens et intensité) des forces exercées sur la bille. On prendra m=50 g et l'angle a =25°.
- La direc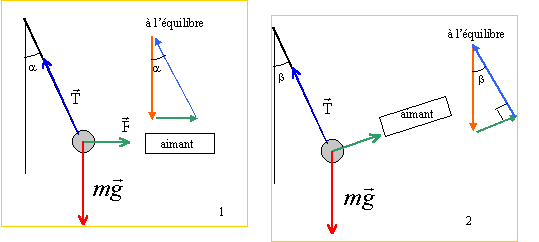tion de l'aimant est placée maintenant perpendiculairement au fil sans que la distance aimant-bille ne varie.Calculer la nouvelle inclinaison du fil.

corrigé

La bille est soumis à trois forces : son poids P = mg = 0,05*9,8 =0,49 N , la tension du fil T et l'action de l'aimant F. A l'équilibre la somme vectorielle des forces est nulle.

figure 1 : cos a =P/T soit T= P/cos a = 0,49 / cos 25 = 1,22 N.

tan a = F/P soit F= P tan a = 0,49 * tan 25 = 0,23 N.

figure 2 : l' action de l'aimant F ne change pas car la distance bille-aimant reste constante

sin b =F/ P = 0,23 / 0,49=0,47 ; b = sin-1(0,47) = 28°.

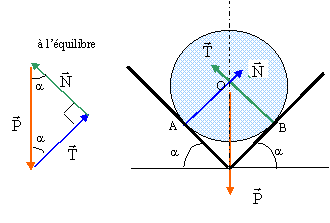
Une sphère de rayon R= 5 cm, de masse m= 0,5 kg est immobile dans une cannelure ( a =45°) On suppose qu'il n'y a aucun frottement. Déterminer les caractéristiques des forces exercées par la cannelure sur la sphère.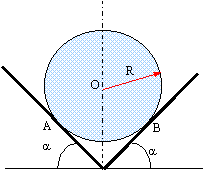

corrigé

La bille est soumis à trois forces : son poids P = mg = 0,5*9,8 =4,9 N , aux actions des supports.. A l'équilibre la somme vectorielle des forces est nulle.

N = T = P cos a = 4,9 cos 45 = 3,46 N.


On pèse un objet métallique au moyen d'un dynamomètre de précison; on trouve F1=10,2N. On immerge cet objet dans l'eau : le dynamomètre indique alors 8,1 N.
- Calculer le poids et la masse de cet objet. (g=9,8 N/kg)

- Calculer le volume V de cet objet.

- En déuire la masse volumique r de cet objet.

corrigé
Le dynamomètre mesure la force qu'exerce la gravité terrestre sur l'objet, c'est à dire son poids (exprimé en Newtons).

Le poids de l'objet est donc de 10,2 N.

Or P= m g soit m = P/g = 10,2 / 9,8 = 1,041 kg. 

Pour connaitre son volume, on fait appel à ce bon vieil Archimède qui nous dit : l'objet reçoit une poussée de bas en haut égale au poids du volume d'eau déplacée. F= reau V g

avec reau masse volumique de l'eau en kg m-3 ; V : volume de liquide déplacé en m3.

On connait la valeur de la poussée (10,2 - 8,1= 2,1 N).

 V= F/ (reau g) = 2,1 / (1000*9,8)=2,14 10-4 m3 = 0,214 L = 214 mL.

masse volumique de l'objet r (kg m-3 ) = masse de l'objet (kg) / volume de l'objet (m3)

r = 1,041/ 2,14 10-4 = 4858 kg m-3.

Un ballon en caoutchouc a pour volume 15 dm3 et pour masse m= 700 g. Il flotte à la surface de l'eau. Déterminer la valeur du volume immergé.
- On le maintient immobile sous l'eau. Quelles sont les caractéristiques de la force exercée ?

Donnée : masse volumique de l'eau reau =1 000kg.m-3.

corrigé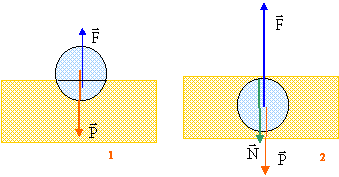

figure 1 : Le ballon est en équilibre, soumis à son poids P et à la poussée d'Archimède F. A l'équilibre ces deux forces sont opposées et ont la même valeur.

P= mg ; poussée F= poids du volume immergé =reau Vg

mg = reau Vimg soit m= reau Vim et Vim= m/ reau = 0,7/1000 = 7 10-4 m3 = 0,7 dm3.

figure 2: Le ballon est en équilibre, soumis à son poids P,à la force musculaire N et à la poussée d'Archimède F. A l'équilibre la somme vectorielle des forces est nulle.

N= F-P

nouvelle valeur de la poussée = reau V ballong = 1000 * 15 10-3*9,8 =147 N

poids : P=mg = 0,7*9,8 = 6,86 N d'où N= 147-6,86 = 140,1 N.


Deux petites sphères, de masse m=0,30 g, sont accrochées chacune à l'extrémité inférieur d'un fil de longueur L=20cm dont l'extrémité supérieur est accrochée à un point fixe O. Elles portent la même charge et, à l'équilibre, les fils font entre eux un angle a=8,0°.

  1. Faire le bilan des forces qui s'exercent sur une sphère.
  2. Ecrire la condition d'équilibre pour une sphère supposée ponctuelle.
  3. En déduire la valeur de la force de Coulomb qui s'exerce sur une sphère.
  4. Calculer la valeur de la charge portée par une sphère.
  5. L'angle a varie-t-il linéairement avec la charge électrostatique portée par les sphères ?
    Donnée: k=9*109S.I.
corrigé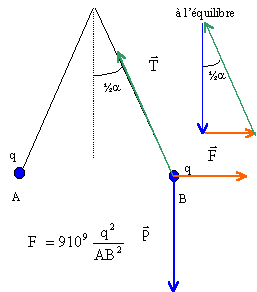

 

à l'équilibre la somme vectorielle des forces est nulle ( voir schéma ci-dessus)

tan (½a)= tan 4 = F/P soit F= P tan(½a) = mg tan(½a) avec la masse n en kg et g = 9,8 N/kg

force de Coulomb F=3 10-4*9,8*tan 4 =2 10-4 N.

calcul de AB : sin(½a)= ½AB/ L soit AB =2L sin(½a) = 2*0,2 sin 4 =0,028 m ; AB²= 0,028² =7,78 10-4 m².

F= 9 109 q²/AB² donne q²= F AB²/(9 109 ) = 2 10-4*7,78 10-4 /(9 109 ) =1,73 10-17

|q| = racine carrée(1,73 10-15)= 4,16 10-9 C.

L'angle a ne varie pas linéairement avec la charge électrostatique portée par les sphères car :

q²= F AB²/(9 109 ) et AB²=4L² sin²(½a) et mg tan(½a) : q²= mg tan(½a) 4L² sin²(½a) /(9 109 ).


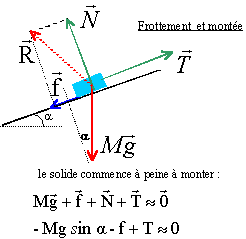
Un bloc parallélépipédique de masse m=200 kg est immobile sur un plan incliné d'un angle a=20° par rapport à l'horizontale.

On veut le mettre en mouvement en tirant sur une corde parallèle à la ligne de plus grande pente du plan incliné. Le coefficient de frottement entre le bloc et le plan incliné est noté µ et a pour valeur 0,5.

  1. La corde n'est pas tendue. On suppose que le bloc est au repos. Déterminer la valeur des composantes normale et tangentielle de la réaction du plan incliné. Le bloc peut-il être immobile ?
  2. On tire sur la corde. Quelle est la valeur de la tension de la corde lorsque le bloc se met en mouvement ?

 

corrigé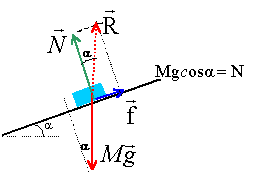

A l'équilibre le poids P = Mg et l'action R du plan sont opposées.

N= Mg cos a =200*9,8 cos 20 =1842 N ;

m= tan a = f/N ; f = m N = 0,5*1842 = 921 N.

comparon cette valeur à Mg sina = 200*9,8*sin 20 = 670 N

le poids tend à faire descendre le solide avec une force de valeur 670 N ; le plan rugueux retient le solide avec une force de valeur 921 N : Donc le solide ne bouge pas.

tension de la corde : T= Mg sin a + f avec f = 921 N et Mg sin a =670 N

T= 670 + 921 = 1591 N.

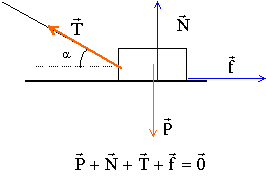
Un voyageur tire une valise de masse = 8,5 kg sur un sol horizontale, à l'aide d'une lainière. La direstion de la lanière fait un angle a = 30° avec l'horizontale. La valise glisse d'un mouvement de translation rectiligne uniforme. La tension de la lanière a pour valeur T=8,0 N.

  1. Faire l'inventaire des forces exercées sur la valise. Donner les carctéristiques connues de ces forces.
  2. Quelle égalité vectorielle doivent vérifier ces forces ? En déduire l'éxistence d'une force de frottement.
  3. Calculer la valeur de cette force de frottement.
corrigé
La valise est soumise à :

son poids, vertical vers le bas, valeur P= mg = 8,5*9,8 = 83,3 N

la tension exercée par la lanière , dirigée suivant la lanière, oblique vers le haut, valeur T= 8 N

l'action du support représentée par les vecteur N et f :

N perpendiculaire au plan, vers le haut, valeur N inconnue.

f : colinéaire à la vitesse mais de sens contraire, valeur inconnue.

Le mouvement étant rectiligne uniforme, alors, d'après le principe d'inertie la somme vectorielle des forces est égale au vecteur nul.

Suivant un axe horizontal orienté dans le sens du mouvement : T cos a -f = 0

suivant un axe vertical orienté vers le haut -P+N+T sin a =0

d'où f =T cos a = 8 * cos30 =6,93 N

et N= P-Tsin a = 83,3-8*sin 30 = 79,3 N.


retour -menu