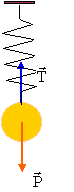|
Balle de tennis – bille accrochée à un ressort En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
|
|
Un parachutiste saute d'un hélicoptère momentanément immobile dans le ciel. Dans tout le problème on supposera sa chute verticale. Avec son équipement, sa masse est de 100 kg (on prendra g=10 N.kg -1). Le graphe ci-dessous donne sa vitesse au cours de la chute en fonction du temps. 
corrigé Avant l'ouverture du parachute, la vitesse augmente ( t<10 s) Après l'ouverture la vitesse diminue 10<t<20 s) puis sa valeur reste constante ( t>20 s) De t=0 à t= 5 s, la courbe est une droite de coeficient directeur 50 / 5 = 10. Entre 0 et 5 s la vitesse et la durée de la chute sont proportionnelles. La seule force qui agit sur le parachutiste est son poids, vertical, vers le bas, appliqué au centre d'inertie du parachutiste, de valeur P=mg = 100*10 = 1000 N. La chute
est libre entre t=0 et t=5 s.
A t >20 s la valeur de la vitesse est constante : le mouvement devient rectiligne uniforme. D'après le principe d'inertie, le parachutiste est pseudo-isolé : la somme vectorielle des forces qui agissent sur lui est nulle. Le poids et la force de frottement sont opposées ( même direction , sens contraire et même valeur 1000 N). vitesse limite de chute : 10 m/s d'après le graphe soit 36 km /h.
|
|||||||||||||||||||||||||
|
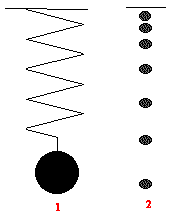
Données : g = 9,8 N/kg ; masse de la balle m = 60 g. On étudie le mouvement d'une balle de tennis lâchée par un cycliste roulant à vitesse constante en ligne droite. On obtient la chronophotographie ci-dessous ; les photos ont été prises toutes les 40 ms. La largeur intérieure du but de handball est de 3,12 m. On numérote les positions de la balle de 1 à 15 (on ne prend pas en compte la position 16, intervenant après un rebond de la balle). 
corrigé Le référentiel d'étude est un référentiel terrestre galiléen. Le mouvement de la balle de tennis est un mouvement parabolique ( la trajectoire est une portion de parabole) La durée de la chute de la balle entre les positions 1 à 15 en seconde vaut 14 intervalle de temps soit 14 * 0,04 =0,56 s. Echelle de la chronophotographie : 10 cm pour la largeur du but soit pour 3,12 m 1 cm correspond donc à 0,312 m. Distance réelle parcourue par la balle au cours de sa chute : 0,312*6,8 = 2,12 m Vitesse moyenne de la balle (m/s) = distance (m) / durée (s) = 2,12 / 0,56 = 3,8 m/s. Principe d'inertie : dans un référentiel galiléen, si un solide est pseudo-isolé : le solide est immobile ou bien son centre d'inertie est animé d'un mouvement rectiligne uniforme et réciproquement. Les distances parcourues par la balle et les durées correspondantes ne sont pas proportionnelles ( voir document) ; la valeur de la vitesse n'est pas constante ( donc mouvement non uniforme). D'après le principe d'inertie, la balle n'est pas pseudo-isolée. Elle est soumise à son poids, vertical, vers le bas, appliqué au centre d'inertie de la balle, de valeur P=mg = 0,06*9,8 = 0,59 N. Le système {cycliste+vélo) se déplace en ligne droite, à vitesse constante. Le centre d'inertie de ce système est animé d'un mouvement rectiligne uniforme. Ce système est pseudo-isolé, d'après le principe d'inertie.
|
||||||||||||||||||||||||||
|
Une bille de masse m = 100 g est suspendue à un ressort vertical à l'aide d'un support. Données : Intensité de la pesanteur : g=9,8 N.kg-1 ; Masse de la Terre M= 5,98 1024 kg ; Rayon de la Terre R = 6,38103 km ; Loi de gravitationnelle universelle : F= G M m/d²avec G = 6,67.10-11 S.I (constante universelle) ; masse en kg et d distance en mètre
corrigé Relation existant entre la valeur du poids P et la masse m de la bille : P(N) = m(kg)*9,8 ( N/kg) P= 0,1*9,8 = 0,98 N. Principe d'inertie : dans un référentiel galiléen, si un solide est pseudo-isolé : le solide est immobile ou bien son centre d'inertie est animé d'un mouvement rectiligne uniforme et réciproquement. La bille étant en équilibre, elle est pseudo-isolée. La bille est donc soumise à une autre force, opposée au poids de la bille, la tension du ressort.
Force gravitationnelle exercée par la Terre sur la bille FTerre/bille = GMm/R² FTerre/bille =6,67.10-11 *5,98 1024 *0,1 / (6,38 106)2 = 0,98 N La force de gravitation a même valeur que le poids de la bille.
T2=8,8 m. période des oscillations d'une bille de masse m2 =
20 g : T2= 8,8 * 0,02 =0,176 ; T=
0,42 s. m= T2/8,8 = 1/8,8 =0,114 kg. mouvement de la bille : le mouvement est rectiligne D'après le chronophotogramme, les distances parcourues pendant des intervalles de temps égaux ne restent pas constantes: Donc le mouvement n'est pas uniforme. Le principe d'inertie indique alors que la bille n'est pas pseudo-isolée. |
||||||||||||||||||||||||||
|
Un elève monte dans un ascenseur avec un pèse-personne et un balai. Le ressort du pèse personne se comprime si on monte le plateau de la balance.
corrigé Le ressort est au repos ( pas de déformation) si le plateau est vide. La déformation du ressort ( dynamomètre étalonné ) est proportionnelle au poids de l'élève : la balance indique le poids de la personne L'élève appuie le balaie au plafond de l'ascenseur immobile, le pèse-personne indique une valeur supérieure au poids de l'élève. L'élève appuie le balai sur le sol de l'ascenceur immobile, le pèse-personne indique une valeur inférieure au poids de l'élève. L'ascenseur démarre en montant, le pèse-personne indique une valeur supérieure au poids de l'élève. L'ascenseur démarre en descendant, le pèse-personne indique une valeur inférieure au poids de l'élève. Le reférentiel de l'ascenseur est non galiléen au démarrage.
|
||||||||||||||||||||||||||
|
|