|
cinétique d'une réaction de complexation - dosage électroargentimétrique d'après bac STL CLPI juin, septembre, Antilles 2003 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Dans un volume Va = 50,0 mL d'une solution aqueuse A d'acide propanoïque de concentration molaire Ca = 0,20 mol.L-1, on ajoute progressivement une solution aqueuse B d'hydroxyde de sodium de concentration Cb = 0,10 mol.L-1.
Constante d'acidité du couple C2H5COOH/ C2H5COO- : pKa = 4,9 corrigé C2H5COOH + H2O = C2H5COO- + H3O+. conservation de l'élément carbone : [C2H5COO-] + [C2H5COOH] = Ca = 0,2 constante d'acidité : Ka = [C2H5COO-] [H3O+] / [C2H5COOH]=10-4,9 = 1,26 10-5. d'après l'équation ci-dessus : [C2H5COO-] = [H3O+] l'acide est peu dissocié dans l'eau : [C2H5COO-] négligeable devant [C2H5COOH] et [C2H5COOH] = 0,2 mol/L [C2H5COO-] [H3O+] / [C2H5COOH] proche de [H3O+]2 / Ca = 1,26 10-5 [H3O+]2 = 1,26 10-5 * 0,2 = 2,51 10-6. [H3O+] =1,58 10-3 mol/L et pH= -log 1,58 10-3 = 2,8. l'approximation [C2H5COO-]
négligeable devant [C2H5COOH] était justifiée.
à l'équivalence : solution de propanoate de sodium ; la solution contient une base, l'ion C2H5COO- , le pH est donc basique la quantité de matière d'acide et la quantité de matière de
soude ajoutée à l'équivalence sont en proportions stoechiométriques CaVa=CbVe
soit Ve = 0,2*50 10-3 / 0,1 = 0,1 L.
la solution contient un couple acide base C2H5COOH/ C2H5COO- tel que [C2H5COOH]=[ C2H5COO-] ; le pH est alors égal au pKa du couple acide base soit pH=4,9. On a une solution tampon : le pH de cette solution ne varie pas par dilution ; le pH de cette solution varie peu lors de l'ajout modéré d'une base ou d'un acide forts. mélanger les solutions 1 et 4 : la solution 1 apporte initialement 50 mmol d'ion propanoate et la solution 4 apporte initialement 25 mmol d'ion oxonium H3O+ Une réaction acide base se produit : C2H5COO- + H3O+ = C2H5COOH + H2O. après réaction il reste 25 mmol d'ion propanoate et il s'est formé 25 mmol d'acide propanoïque.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On s'intéresse à la solubilité du chromate d'argent, Ag2CrO4, dans divers milieux. Données (à 25 °C) Masse molaire du chromate d'argent : 331,8 g.mol-1 Produit de solubilité du chromate d'argent : KS = 1,6 10-12 Constante de dissociation du complexe [Ag(NH3)2]+ : KD = 6,3 10-8
corrigé Ag2CrO4 solide = 2Ag+ + CrO42-. Ks = [Ag+]2[CrO42-] ; on pose s= [CrO42-] ; solution électriquement neutre : [Ag+] = 2 [CrO42-] d'où [Ag+] = 2 s Ks = (2s)² s = 4 s3 = 1,6 10-12 soit s3 = 0,4 10-12 prendre la racine cubique : s = 7,35 10-5 mol/L multiplier par la masse molaire du chromate d'argent : s= 7,35
10-5 *331,8 =2,44 10-2
g/L.
s'= [CrO42-] ; [Ag+] = 2s'+0,1 voisin 0,1 Ks= [Ag+]2[CrO42-] = 0,1² s' = 1,6 10-12 s'= 1,6 10-10 mol/L ou bien s'= 1,6 10-10*331,8
= 5,3 10-8 g/L.
Ag2CrO4 solide + 4 NH3 = 2[Ag(NH3)2]+ + CrO42- (1) constante de dissociation KD associée à l'équilibre : [Ag(NH3)2]+= Ag+ +2NH3. KD= [Ag+][NH3]2 / [[Ag(NH3)2]+] Qté de matière de chromate d'argent : 10 / 331,8 = 3 10-2 mol Qté de matière d'ammoniac d'après (1) : 4*3 10-2 = 0,12 mol 0,12 mol dans 0,2 L d'où [NH3]=0,12 / 0,2 = 0,6 mol/L.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On se propose d'étudier la réaction de complexation des ions chrome (III) par l'EDTA, en solution aqueuse maintenue à pH = 5,1. Données (à 25 °C) : L'EDTA est introduit sous forme de sel disodique Na2H2Y qui se dissocie totalement en ions Na+ et H2Y2- en solution. · pKa de l'EDTA, H4Y, en solution aqueuse : pKa1 (H4Y/H3Y-) = 2,0 ; pKa2 (H3Y-/H2Y2-) = 2,7 ; pKa3 (H2Y2-/HY3-) = 6,2 ; pKa4 (HY3-/Y4-) = 10,3 · Constante de dissociation de l'ion complexe [CrY]- : KD = 1,0 10-23.
corrigé 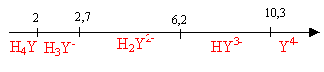
à pH=5,1 , H2Y2- prédomine. Ka3 associé à l'équilibre acide base H2Y2-+ H2O=HY3-+ H3O+ : Ka3 = [HY3-][H3O+] / [H2Y2-] (1) Ka4 associé à l'équilibre acide base HY3- + H2O=Y4-+ H3O+ : Ka4 = [Y4-][H3O+] / [HY3-] (2) (1) donne : [HY3-] =Ka3[H2Y2-] / [H3O+] (2) donne : [Y4-] =Ka4[HY3-]/ [H3O+] = Ka4Ka3[H2Y2-] /([H3O+])² [H2Y2-] = 0,1 ; [H3O+] = 10-5,1 = 7,94 10-6 mol/L ; Ka4= 10-10,3 =5 10-11 ; Ka3= 10-6,2 =6,3 10-7 ; [Y4-] = 6,3 10-7 *5 10-11 *0,1 / (7,94 10-6)²= 5 10-8 mol/L. [CrY]- = Y4- + Cr3+ constante associée KD =[Cr3+][Y4-] / [[CrY]-] = 10-23 [Y4-] =5,0 10-8 mol/L ; [Cr3+]*5,0 10-8 / [[CrY]-] = 10-23 ; [Cr3+] / [[CrY]-] =10-23 / (5 10-8 )= 2 10-16. [[CrY]-] =[Cr3+] /2 10-16 = 5 1015 [Cr3+] conservation de l'élément chrome : [Cr3+] + [[CrY]-] = 3 10-3 =[Cr3+] + 5 1015 [Cr3+] = 3 10-3; [Cr3+] = 6 10-19 mol/L donc la réaction de complexation est totale ( pratiquement tous les ions chrome (III) ont disparu de la solution) vitesse de formation du complexe v= k [H2Y2-] [Cr3+]. H2Y2-est en large excès devant Cr3+ ; [H2Y2-] peut être considérée comme une constante égale à [H2Y2-]0 par suite v = k [H2Y2-]0 [Cr3+] = k'[Cr3+]
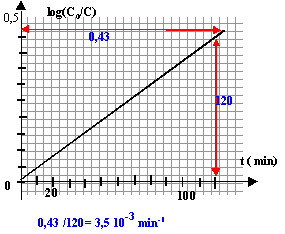
la courbe est une droite, donc la loi log(C0/C) = k't est bien vérifiée
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
On se propose d'étudier le dosage électroargentimétrique d'une solution (S) contenant des ions chlorure et des ions iodure : - une prise d'essai de 100,0 mL de solution (S) contenant 5,0 10-3 mol.L-1 de chlorure de potassium KCl et 5,0 10-3 mol.L-1 d'iodure de potassium KI est placée dans un bécher ; - une électrode d'argent est plongée dans cette solution ; un dispositif permet d'en mesurer le potentiel par rapport à l'électrode standard à hydrogène ; - on verse une solution de nitrate d'argent AgNO3 suffisamment concentrée pour considérer que le volume total est constant, et on mesure le potentiel de l'électrode d'argent. Données (à 25 °C) : Produits de solubilité : KS1 (AgI) = 1,5 10-16 ; KS2 (AgCl) = 1,5 10-10. Potentiel standard : E°(Ag+/Ag(s)) = 0,80 V (RT/F).ln(x) = 0,06 log(x), en V
corrigé potentiel de l'électrode d'argent E = E°(Ag+/Ag(s)) + 0,06 log [Ag+] tant qu'il y a des ion iodure en solution : [Ag+] = KSI/[I-] E = E°(Ag+/Ag(s)) + 0,06 log (KSI/[I-]) or [I-] diminue au cours du dosage ; KSI est constant à température donnée ; KSI/[I-] va augmenter ; log (KSI/[I-]) va augmenter : donc le potentiel E augmente. tant qu'il y a des ion chlorure en solution : [Ag+] = KS2/[Cl-] E = E°(Ag+/Ag(s)) + 0,06 log (KS2/[Cl-]) même remarque que pour les ions iodures. lorsque Ag+
est en excès : [Ag+] augmente ; log [Ag+] aumente ainsi que le potentiel
E.
Ag+ + I- = AgI solide , constante associée : K1 = 1/ ( [Ag+]/[I-] )= 1/Ks1 = 1,5 10-16 = 6,67 1015. Ag+ + Cl- = AgCl solide , constante associée : K2 = 1/ ( [Ag+]/[Cl-] )= 1/Ks2 = 1,5 10-10 = 6,67 109. K1 est très supérieur à K2 : donc AgI
précipite le premier et ensuite quand il n'y aplus d'ion iodure en
solution AgCl commence à précipiter.
E = E°(Ag+/Ag(s)) + 0,06 log (KSI/[I-]fin) E1= 0,8 + 0,06 log(1,5 10-16 / 5 10-6) = 0,8 + 0,06 log(3 10-11 )= 0,8-0,63 = 0,17 V. Lorsque le chlorure d'argent commence à précipiter : [Cl-] voisin de 5 10-3 mol/L E = E°(Ag+/Ag(s)) + 0,06 log (KS2/[Cl-]) E2= 0,8 + 0,06 log(1,5 10-10/ 5 10-3) = 0,8 + 0,06 log(3 10-8 )= 0,8-0,45 = 0,35 V. cette valeur est assez différente de la précédente : on peut donc doser séparément les ions chlorure et iodure par précipitation. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Données à 25 °C · Masses atomiques (g.mol-1) : Na = 23,0 F = 19,0 · Constante d'acidité : HF/F- : pKa = 3,2 · Produit ionique de l'eau : pKe = 14,0 · Le fluor (Z=9) possède un seul isotope naturel de nombre de masse 19
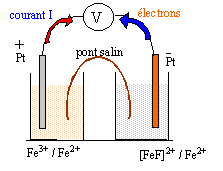
OXYDO-REDUCTION ET COMPLEXATION Données à 25 °C · Produit ionique de l'eau : pKe = 14,0 · Sel de Mohr : FeSO4,(NH4)2SO4, 6 H2O Alun ferrique : Fe2(SO4)3,K2SO4, 4 H2O · Potentiel standard : E°(Fe3+/Fe2+) = 0,77 V · RT/F ln x = 0,06 lg x, en V On se propose de déterminer la constante de dissociation (Kd) du complexe [FeF]2+. Pour cela on réalise les deux demi-piles suivantes : Demi-pile n°1 : une lame de platine plongeant dans une solution aqueuse contenant des ions Fe3+ et Fe2+ à la même concentration, 1,0 10-2 mol.L-1 pour chacune de ces espèces. Demi-pile n°2 : une lame de platine plongeant dans 100 mL de solution aqueuse contenant 1,0 10-3 mol de sel de Mohr et 5 10-4 mol d'alun ferrique à laquelle on ajoute 1,0 10-2 mol d'ions fluorure, sans variation de volume. On suppose que seul l'ion complexe [FeF] 2+ est formé.
corrigé La structure du noyau de fluor : Z=9 donc 9 protons positifs A= 19 donc 19-9=10 neutrons. structure électronique de l'atome : 2 électrons sur le niveau n=1 et 7 électrons sur le niveau n=2 (K2L7) donc seconde période et 17 ème colonne : le fluor appartient à la famille des halogènes. HF+H2O = F-+H3O+. Ka = 10-3,2 = 6,3 10-4 = [F-][H3O+] /[HF] solution électriquement neutre ( HO- négligeable en milieu acide) : [F-]=[H3O+] conservation de l'élément fluor : [HF]+[F-] = 0,1 mol/L acide fluorhydrique peu dissocié donc [F-] négligeable devant [HF] : [HF] voisin 0,1 mol/L 6,3 10-4 =[H3O+]2 /0,1 ; [H3O+]2 = 6,3 10-5 ; [H3O+] = 7,93 10-3 mol/L l'approximation "[F-] négligeable devant [HF] " est justifiée. pH= - log(7,93 10-3
)=2,1.
Qté de matière NaF : 2,1 / (23+19)= 0,05 mol [Na+]=[F-]=Qté matière (mol) / volume solution (L) =0,05/0,25 = 0,2 mol/L. solution C : Qté de matière : HF : 0,15*0,1 = 0,015 mol dans 0,25 L ; [HF]=0,015/0,25=0,06 mol/L F- : 0,1*0,2 = 0,02 mol dans 0,25 L ; [F-] = 0,02/0,25 = 0,08 mol/L la solution C contient le couple acide base HF / F- tel que [HF] voisine de [F-]. C est une solution tampon dont le pH varie peu lors de l'ajout modéré d'acide ou de base ; dont le pH ne varie pas par dilution. calcul du pH de la solution C : pH=pKa (HF/F-) + log ([F-] /[HF]) pH=3,2 + log(0,08
/ 0,06)=3,32.
E1 = E°(Fe3+/Fe2+) + 0,06 log ([Fe3+]/[Fe2+]) or [Fe3+]=[Fe2+] donc E1 = E°(Fe3+/Fe2+) =0,77 V. [Fe2+] = Qté de matière (mol) / volume solution (L) =10-3 / 0,1 = 0,01 mol/L l'alun ferrique conduit à : Fe2(SO4)3= 2 Fe3++ 3 SO42-. [Fe3+] =2* 5 10-4 /0,1 = 0,01 mol/L [FeF]2+ :anion fluoroferrate (III) E= E1-E2 = 0,25 V soit E2 =0,77-0.25 = 0,52 V. E2 = E°(Fe3+/Fe2+) + 0,06 log ([Fe3+]/[Fe2+]) avec [Fe2+] =0,01 mol/L 0,52=0,77+0,06 log ([Fe3+]/0,01) ; log ([Fe3+]/0,01) = -0,25/0,06 = -4,16 ([Fe3+]/0,01 = 10-4,16 =6,9 10-5 ; [Fe3+] = 6,9 10-7 mol/L. [FeF]2+ = Fe3+ + F- constante associée Kd= [Fe3+] [F-]/ [[FeF]2+] conservation de l'élément fer (III) : [Fe3+] + [[FeF]2+] = 0,01 mol/L donne :[FeF]2+] = 0,01 -6,9 10-7 = 0,01 mol/L conservation de l'élément fluor : [F-]+[[FeF]2+] = 0,01/0,1 = 0,1 mol/L donne [F-] = 0,1 -[[FeF]2+] = 0,1 -0,01 = 0,09 mol/L Kd= [Fe3+] [F-]/ [[FeF]2+]= 6,9 10-7 *0,09 /0,01 = 6,21 10-6.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|