|
d'après bac Sti mécanique 2005 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
|||
|
|||
|
|
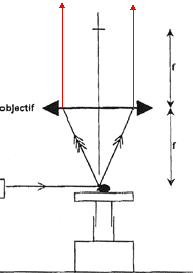
II est possible de réaliser des photos très nettes d'objets de très petite taille à l'aide de la technique schématisée ci-dessous : 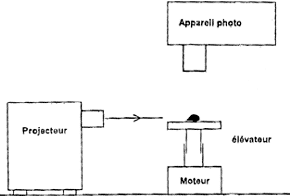 Le projecteur émet un fin pinceau lumineux. Un élévateur déplace verticalement un objet, à vitesse constante, durant la durée d'ouverture du diaphragme de l'appareil photo. Le cahier des charges impose une élévation à vitesse réglable mais constante, sans à coups. La solution choisie est un guidage rectiligne poussé par une vis, en rotation grâce à un petit moteur à courant continu alimenté par un convertisseur. |
||
|
Partie A : étude du moteur à courant continu (12 points) Le moteur à courant continu utilisé est à aimants permanents avec les caractéristiques suivantes : tension d'alimentation nominale : UN = 24 V ; résistance d'induit : r = 5,0 W. I. Relation fondamentale :
II Essai à vide du moteur : On réalise un essai du moteur à vide, c'est-à-dire désaccouplé de l'élévateur ; on relève : UV = 24 V ; IV = 100 mA ; nV = 2350 tr / min.
III. Essai en charge du moteur couplé à l'élévateur seul L'arbre du moteur entraîne maintenant le mécanisme de l'élévateur. On relève : UN = 24 V ; IN = 2,0 A ; nN = 1500 tr / min.
IV Essai en charge du moteur couplé à l'élévateur portant un objet
corrigé 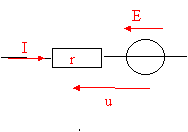
U=E+rI f.é.m EV pour cet essai à vide : EV = UV -rIV= 24-5*0,1=23,5 V. puissance totale absorbée PV = UV IV = 24 * 0,1 = 2,4 W. pertes par effet Joule PJV = r IV2 = 5 * 0,12 = 0,05 W = 50 mW. PV = PUV + PjV + Pf + Pm avec PUV = 0 et Pf + Pm = PCV d'où pertes
collectives PCV = PV - PjV = 2,4 -
0,05 = 2,35 W.
puissance totale absorbée PN = UN IN = 24 * 2 = 48 W. pertes par effet Joule PJN = R IN2 = 5 * 22 = 20 W. les pertes collectives PC sont proportionnelles à la fréquence de rotation de l'arbre : 2,35/2350*1500 = 1,5 W. puissance utile PUN du moteur : PN - PjN - PCN = 48 - 20 -1,5 = 26,5 W. rendement du
moteur 26,5/48 proche de 0,5 ( 50%)
couple utile Ti = couple résistant Tr = couple électromécanique T - couple du aux pertes constante TP. En plaçant un objet sur l'élévateur, Tr augmente, T augmente donc I augmente. Or E = k W = U - r.I donc pour augmenter W , il faut augmenter U, la tension aux bornes de l'induit, sachant que I est constant.
|
|||
|
Partie B : alimentation du moteur (5 points) Le moteur est alimenté par un convertisseur, lui-même en aval d'un transformateur supposé parfait. 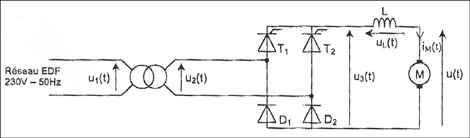
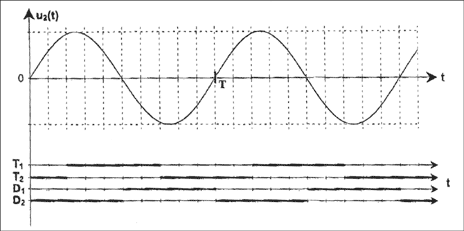
corrigé Le transformateur ne modifie pas la fréquence. La fréquence de u2(t) est 50 Hz Valeur efficasse de la tension u2(t) : rapport de transformation * valeur efficasse de u1(t) soit 0,1*230 = 23 V. fonction et nom du convertisseur qui a pour tension d'entrée u2(t) et tension de sortie u3(t) : pont mixte conversion "alternatif-continu").
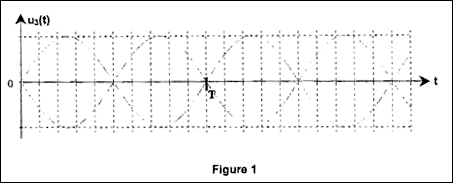
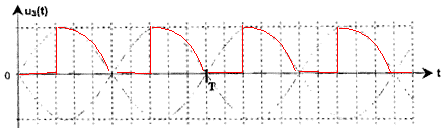
Quand T1 et D2 conduisent, u3 = u2 ; quand T2 et D1 conduisent, u3 = - u2 Quand T1 et D1 conduisent, u3 = 0 ; quand T2 et D2 conduisent, u3 = 0 la période de la tension u3(t) est égale à la moitié de la période T avec T= 1/50 = 0,02 s = 20 ms période de u3(t) = 10 ms. angle q de retard à l'amorçage des thyristors : q correspond à deux carreaux alors qu'une période T correspond à 10 carreaux q correspond donc à T/5 ; or une période correspond à 2p radians q correspond donc à 2p/5 radians. uL(t) = L diM(t) / dt avec cans ce cas iM(t) = constante donc uL(t) =0 valeur moyenne de u3(t) est égale à celle de u(t) : u3(t) = uL(t) + u(t) soit < u3(t) > = < uL(t) > + < u(t) > or < uL(t) > = 0 donc < u3(t) > = < u(t) >
|
|||
|
Partie C : objectif de l'appareil photographique (3 points) L'objectif de l'appareil photographique est assimilé à une lentille convergente de distance focale f = 20 cm.
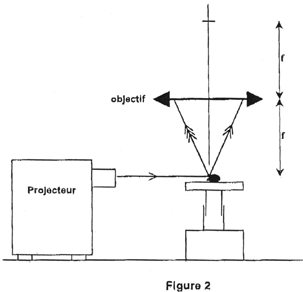
corrigé la vergence s'exprime en dioptrie ( symbol d) la vergence est l'inverse de la distance focale image exprimée en mètre v= 1/ 0,2 = 5 d des rayons incidents passant par le foyer principal image, émergent parallèlement à l'axe optique principal.
|
|||
| |
|||
|
|