|
physique : 1 h 20 points; chimie ½h 10 points ;d'après concours kiné Assas 2005 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||
| .
. |
||
|
||
|
|
Il est demandé l'expression des valeurs littérales avant tout calcul numérique. La médaille d'or du lancer du poids fut remporté avec un jet d'une distance d= 21,16 m. Le poids sphérique, homogène, a une masse m = 7,26 kg. L'aire de lancement au sol est matérialisée par un cercle métallique de centre C et de diamètre D= 2,14 m, à la phériphérique duquel est placé un butoir B. La portée du lancer est mesurée à partir du centre C du cercle. On assimilera le poids à son centre d'inertie G, affecté de la masse m. A l'issue de la phase d'élan, le poids est abandonné en A, à la hauteur OA= h= 2,00 m au dessus du sol horizontal, à la distance BO= 0,350 m, en avant du butoir B. Le bras qui lance fait alors un angle a= 45 ° avec l'horizontale. Le point d'impact est noté M. 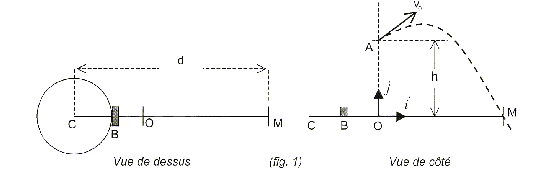 On assimile la résistance des forces de frottements dues à l'air à une force R= ½rCxSv² où r est la masse volumique de l'air 1,9 10-3 kg m-3, S l'aire de la section équatoriale de la sphère de valeur 1,13 10-2 m², Cx un coefficient caractéristique de la forme de l'objet de valeur 0,500 SI et v la valeur de la vitesse.
corrigé Cx = 2R/ (rSv²) R force en N soit masse * accélération ( kg m s-2) masse volumique : kg m-3 ; S en m² ; v² longueur ² / temps ² soit m² s-2 : (rSv²) s'exprime en : kg m s-2 . en conséquence Cx est sans dimension. poids P= mg = 7,26*9,81 = 71,15 N R= 0,5*0,5*1,9 10-3 * 1,13 10-2 * 102= 5,3 10-4 N P/R = 71,15/ 5,3 10-4 = 1,3 105. La résistance de l'air est négligeable devant le poids.
le vecteur vitesse est une primitive du vecteur accélération ( v0cos a ; -gt +v0 sin a ) le vecteur position est une primitive du vecteur vitesse : x(t) = v0cos a t ; y(t) = -½gt² + v0 sin a t + h. mouvement rectiligne uniforme suivant Ox et mouvement uniformément accéléré suivanr Oy. t = x / v0cos a, repport dans y(t) : trajectoire : y = -½g x²/( v0cos a)² + x tan a + h. y= -9,8 x² / v0² + x +2 au point M : xM= 21,16 - 0,35-1,07 = 19,74 m ; yM=0 0= -9,8 xM² / v0² + xM +2 v0² = 9,8 xM² /(xM +2)= 9,8 * 19,74² / 21,74 = 175,65 ; v0 =13,25 m/s. durée du trajet t = xM / v0cos a = 19,74 /( 13,25*0,7) =2,1 s. vitesse en M : vx= v0cos a = 13,25*0,7 = 9,27 m/s vy = -gt +v0 sin a = -9,8 *2,1+ 13,25*0,7 = -11,3 m/s v²M=
9,27²+11,3² = 213,84 et vM= 14,62 m/s.
énergie mécanique initiale : ½mv0² + mgh énergie mécanique finale ½mvM² seul le poids travaille, l'énergie mécanique se conserve : ½mv0² + mgh = ½mvM² vM² = v0² + 2gh = 175,6 + 2*9,8*2 = 214,8 ; vM= 14,65 m/s (accord des résultats)
|
|
|
corrigé fission de gros noyaux instables,( uranium 235) conduisant à des noyaux plus petits et plus stables. fusion des petits noyaux instables ( hydrogène et ces isotopes) pour conduire à des noyaux plus gros et plus stables. fission nucléaire conservation du nombre de neutrons : 235 + 1 = 139 + 94 + y soit y = 3 conservation de la charge : 92 = x+ 38 soit x= 54 variation de masse Dm= m(23592U )-[m(139xXe) + m(9438Sr) + 2 m(10n)] Dm= (3,902 - 2,306-1,559-2*0,01675) 10-25 = 3,5 10-28 kg. E= Dm c² = 3,5 10-28 * 9 1016 = 3,15 10-11 J = 3,15 10-11 / 1,602 10-19 eV = 1,966 108 eV = 196,6 MeV. cette énergie est emportée par les trois neutrons émis sous forme d'énergie cinétique ½mv² v² = 2E/(3m)= 2*3,15 10-11 / (3*
1,675 10-27)= 1,25 1016 ;
v = 1,12 108
m/s.
énergie électrique produite par jour : 900 106 * 24*3600 = 7,776 1013 J énergie thermique libérée : 7,776 1013 / 0,33 = 2,356 1014 J soit 2,356 1014 / 1,602 10-19 = 1,472 1033 eV = 1,472 1027 MeV. nombre de réactions : 1,472 1027 / 200 = 7,36 1024. à chaque réaction est mis en jeu un noyau d'uranium de masse : 3,9 10-25 kg : masse d'uranium 235 : 3,9 10-25 * 7,36 1024 = 2,87 kg / jour. |
||
|
L'oeil est équivalent à une lentille L convergente, de centre optique O, associé à un écran E ( la rétine). On observe un objet AB parallèle à cette lentille, A étant sur l'axe optique de L. Un oeil normal peut "accommoder", c'est à dire donner une image A'B' nette, lorsque l'objet est situé à une distance du centre optique comprise entre 25 cm et l'infini.
corrigé 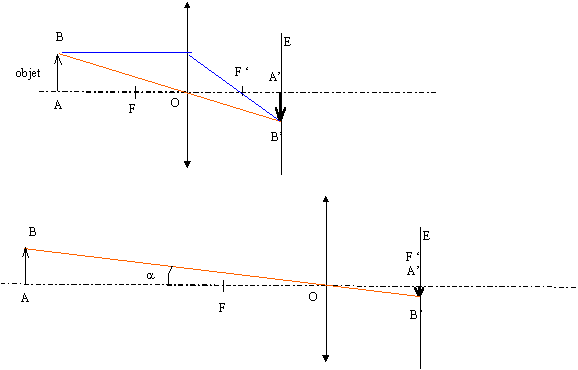
objet à l'infini, alors l'image se forme au foyer principal image de la lentille f' = 1 /C1 = 1/60 = 1,67 10-2 m = 1,67 cm. AO + OA' = D formule de conjugaison : C2 = 1/ OA' - 1/ OA ( les mesures algèbriques sont écrites en bleu et en gras) avec OA'= 1,67 10-2 m et OA = -0,25 m C2 = 100/ 1,67 - 1 / (-0,25) = 64 dioptries. tan a voisin de a (radian) = h/f' soit h = f' a ; f' = 1/60 m et a = 3*3,14/180 =0,0524 rad h= 0,0524/60 = 8,7 10-4 m.
|
||
|
Un volume Va = 10 mL d'une solution A d'acide monochloroéthanoique est dosé, en présence de phénolphtaléine ( zone de virage [8,2 ; 10]), par une solution B de soude de concentration Cb= 0,080 mol/L. A l'équivalence le volume de solution B versé est Vb= 12,5 mL. On note S la solution obtenue à l'équivalence et V son volume total.
corrigé ClCH2-COOH + HO- = ClCH2-COO- + H2O à l'équivalence les quantités de matière des réactifs sont en proportions stoéchiométriques Ca Va = Cb Vb soit Ca = Cb Vb / Va = 0,08*12,5 / 10 = 0,1 mol/L. a = [A-]éq / ([AH]éq + [A-]éq) = [A-]éq / C. conservation de A : [AH]éq + [A-]éq = CaVa/ V = C 1 - a = 1- [A-]éq / C = (C- [A-]éq )/ C =[AH]éq / C. pH = pKa + log ([A-]éq /[AH]éq ) pH = pKa + log (a / (1 - a)) si Ka = 1,8 10-4 alors pKa = -log(1,8 10-4)= 3,745 ; a proche de 1 pH = 3,745 + log ( 1 / 3,53 10-5) = 8,2. l'indicateur a été bien choisi car sa zone de virage contient le pH du point équivalent.
|
||
|
Les phéromones sont des molécules secrétées par certains insectes pour communiquer. L'acétate d'isoamyle ( éthanoate de 3-méthylbutyle)est une phéromone d'alarme chez l'abeille qui déclenche une attitude agressive chez celles qui la reçoivent. Sa formule semi-développée est représentée ci-dessous : 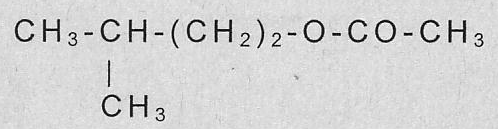
masse molaire (g/mol) : alcool : 88 ; acide : 60 ; phéromone : 130. corrigé 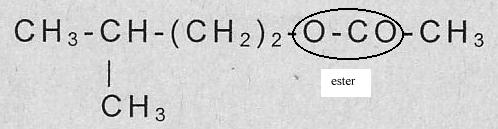
CH3-COOH + CH3-CH(CH3)-CH2-CH2OH = CH3-COO-(CH2)2-CH[CH3 ]2+ H2O acide éthanoïque +3-méthylbutan-1-ol donne éthanoate de 3-méthylbutyle + eau Qté de matière (mol) = masse (g) / masse molaire (g/mol) n( alcool)= 20/ 88 = 0,227 mol n(acide) = 10/60 = 0,167 mol ( en défaut) on peut obtenir au plus ( si réaction totale) 0,167 mol d'ester n( ester) = 14/130 = 0,108 mol ( quantité réelle) rendement r = quantité réelle(mol) /quantité théorique (mol)= 0,108 / 0,167 = 0,645 soit 64,5 %. n( alcool) restante : 0,227 - 0,108 = 0,119 mol soit : 0,119*88 = 10,47 g n( acide) restant : 0,167-0,108=0,059 mol soit 0,059*60 = 3,52 g.
|
||
|
|