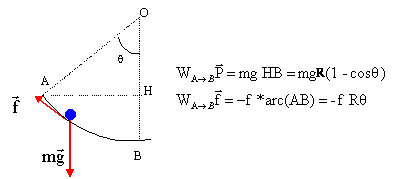Aurélie dec 04

Energie mécanique, projectile, pendule

diffraction, interférences ; condensateur.

d'après concours technicien météo 98.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .

.
.


On se propose d'étudier l'évolution d'un mobile (M) de masse m= 500 g au cours du parcours proposé ci-dessous. Au départ le mobile se trouve en A. Il est laché sans vitesse initiale. Les forces de frottement sur l'arc de cercle AB, de rayon R=80 cm, sont considérées comme constantes, opposées à la vitesse et représentent r=25% du poids du mobile. g =9,8 m/s² ; q=45°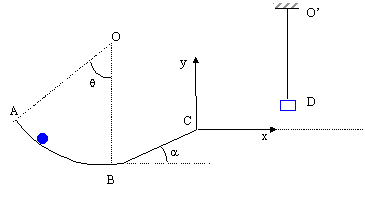

  1. Représenter les forces s'exerçant sur M au cours du trajet AB.
  2. Calculer la vitesse du mobile en B.
  3. Le mobile doit maintenant parcourir la longueur L= 10 cm du tremplin compris entre les points B et C, incliné d'un angle a=10° par rapport à l'horizontale. On néglige les forces de frottement sur cette portion BC. Quelles sont les caractéristiques du vecteur vitesse du mobile M au point C ? Donner l'expression de la vitesse VC en fonction de g, R, r, q, a et L.
  4. Le mobile partant de C arrive dans un petit panier repéré par le point D. Quelle doit être la position du point D dans le repère (C, x, y) pour que le mobile arrive en D avec le minimum d'énergie cinétique ?
    - Le transfert d'énergie cinétique est supposé total. Le panier suspendu par unfil de longueur L'= 2 m se met à osciller. On considère que l'ensemble fil - panier - mobile constitue un pendule simple de masse m=500 g. Les forces de frottements sont négligées. Déterminer l'angle     b d'écartement maximum du pendule simple par rapport à la verticale en fonction de VC, a, g et L'. Calculer la période propre T0 du pendule simple.
corrigé
Vitesse du mobile en B :

q =0,785 rad ian

f = r mg

DEc= ½ mVB², la vitesse initiale en A étant nulle
La variation d'énergie cinétique entre A et B est égale à la somme des travaux des forces :

½ mVB² = mgR(1-cosq) -f R q = mgR(1-cosq) -r mg R q

VB² = 2 gR(1-cosq-r q).

VB² = 2*9,8*0,8 ( 1-cos45-0,25*0,785) = 1,517 ; VB= 1,23 m/s.

La vitesse VC en fonction de g, R, r, q, a et L :

Le vecteur vitesse étant toujours tangent à la trajectoire, est parallèle au plan incliné et dirigé vers le haut du plan

ordonnée : VCy= VC sin a ; abscisse : VCx= VC cos a ;

La variation d'énergie cinétique entre B et C est égale à la somme des travaux des forces ;

seul le poids travaille car l'action du plan est perpendiculaire au plan

travail résistant du poids ( ça monte) entre B et C : -mg L sin a.

½mVC²-½mVB²= -mg L sin a ; VC² = VB² -2g L sin a.

remplacer VB² par : VB² = 2 gR(1-cosq-r q).

VC² = 2 gR(1-cosq-r q)-2g L sin a.

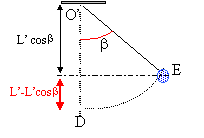
Position du point D dans le repère (C, x, y) pour que le mobile arrive en D avec le minimum d'énergie cinétique :

l'énergie cinétique est minimum si la vitesse est minimum : au sommet de la trajectoire parabolique, l'ordonnée de la vitesse est nulle et l'abscisse de la vitesse vaut VC cos a. La vitesse prend alors sa plus petite valeur.

Energie cinétique minimum : ½mVC² cos² a.

angle b d'écartement maximum du pendule simple :

L'énergie cinétique finale en E est nulle pour l'angle b. DEc= -Ec initiale en C=- ½mVC²cos² a

seul le poids travaille entre D et E ; la tension du fil , perpendiculaire à la vitesse ne travaille pas.

travail du poids résistant ( ça monte) : -mgL'(1-cosb)

th. de l'énergie cinétique : - ½mVC²cos² a = -mgL'(1-cosb) ; VC² cos² a = 2gL'(1-cosb) ;
(1-cosb) = VC² cos² a /( 2gL') ; cosb = 1-VC²cos² a /( 2gL').

période propre T0 du pendule simple : T0 = 2p(L'/g)½.

T0 = 2*3,14*(2/9,8)½ = 2,83 s.


Diffraction, interférences
  1. Une fente verticale, de largeur a = 5 10-4 , est éclairée par un faisceau laser de longueur d'onde l=630 nm. L'écran d'observation est placé à une distance D= 4 m de la fente. Faire un schéma du montage et de la figure de diffraction.
    - Calculer en degré, la largeur angulaire     a de la tache centrale observée sur l'écran.
    - Calculer la largeur d de cette fente centrale.
  2. La fente de largeur a est remplacée par deux fentes très fines S1 et S2 parallèles, distantes de 0,5 mm et éclairée par un laser. L'écran est maintenant situé à une distance D= 1 m des fentes. Les fentes et l'écran sont placés perpendiculairement à la direction de propagation du pinceau lumineux. Cet ensemble constitue un dispositif d'Young.
    - Décrire à l'aide d'un schéma les phénomènes observés sur l'écran.
    - Soit O le point d'intersection entre l'écran et la médiatrice du segment joignant le centre des fentes. Un point M est repérer par son abscisse x sur un axe d'origine O et passant par M. On admet que la différence de marche     d= S2M-S1M=ax/D. Calculer la position, en fonction de l'ordre k, des franges brillantes sur l'écran.
    - Evaluer l'interfrange i.
  3. Une lame de verre d'épaisseur e=1 mm et d'indice de réfraction n=1,5 est placée sur letrajet du faisceau issu de S1.
    - Calculer la distance parcourue par la lumière dans l'air pendant la durée     t qui lui est nécessaire pour traverser la lame ( nair = 1).
    - En déduire l'augmentation de durée     Dt du parcours du faisceau issu de S1 qui traverse la lame.
    - Exprimer la nouvelle différence de marche     d ' en un point M de l'écran sachant que d '= S2M-S1M=d -cDt ( c : célérité de la lumière dans le vide).
    - Calculer la différence de marche au point O. Quelle luminosité est observée en ce point ?
  4. Cette même lame est maintenant placée sur le trajet du faisceau issu de S2. Calculer la différence de marche d ''= S2O-S1O des deux ondes issues de S1 et S2 au point O par une méthode analogue.
  5. Donner les positions de la frange brillante centrale dans les trois cas suivants : Fentes S1 et S2 sans lame ; fente S1 avec lame d'épaisseur e = 0,01 mm et fente S2 sans lame ; fente S2 avec lame d'épaisseur e = 0,01 mm et fente S1 sans lame
corrigé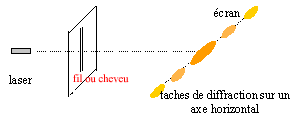

Largeur angulaire a de la tache centrale : a = 2l/a = 2*630 10-9 / 5 10-4 = 2,52 10-3 rad.

2,52 10-3 *180 / 3,14 = 0,144 °.

largeur d de cette fente centrale tan a voisin a = d/D soit d= D a (radian) = 4* 2,52 10-3 = 10-2 m = 1 cm.

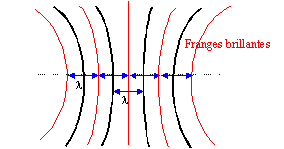
On observe des interférences, une alternance de taches brillantes et sombres.

Si l'ordre d'interférence est un entier ( la différence de marche est un multiple de la longueur d'onde), les interférences sont constructives ( franges brillantes : éclairement maximal).

k=d/l =ax/(Dl ) soit x =k l D/a avec k = 0, 1, -1, 2, -2, 3...

interfrange i =l D/a = 630 10-9 * 1 / 5 10-4 = 1,26 10-3 m.

durée de la traversée d'une épaisseur e de verre : t = e/ v avec v = c/n ; t = ne / c

Pendant cette durée t la lumière traverse une épaisseur d'air égale à : ct = ne.

Augmentation de durée Dt du parcours du faisceau issu de S1 qui traverse la lame : Dt= (n-1)e/c.

différence de marche d' = d -cDt =d -(n-1)e.

différence de marche au point O (d=0) : d' = - (n-1)e .

calcul de l'ordre d'interférence en O : k=d'/l = -(n-1) e /l = -(1,5-1)10-3 / 630 10-9 =793,6

cet ordre est proche d'un demi entier, donc en O la frange observée est presque noire.

d ''= S2O-S1O= cDt =(n-1)e .

Fentes S1 et S2 sans lame : frange brillante centrale en O.

fente S1 avec lame d'épaisseur e = 0,01 mm et fente S2 sans lame ou fente S2 avec lame d'épaisseur e = 0,01 mm et fente S1 sans lame.

L'ensemble du système de franges est déplacé du coté de la lame à l'abscisse x0 telle que :

ax0/D= (n-1)e ; x0=(n-1) e D/a = (1,5-1) 10-5 *1 / 5 10-4 = 10-2 m = 1 cm.


Condensateur
  1. Un condensateur de capacité C= 1 mF est branché en série avec un conducteur ohmique de résistance R= 220 W, un interrupteur et un générateur de tension constante de f.e.m E=5 V et de résistance interne négligeable.
    - Faire un schéma du montage.
    - Le condensateur étant déchargé on abaisse l'interrupteur à la date t=0. Ecrire l'équation différentielle régissant la tension aux bornes du condensateur en fonction du temps.
    - Vérifier que la solution de cette équation peut s'écrire U= A(1-exp(Bt)) où t est le temps et A, B des constantes que l'on exprimera en fonction de E, R et C.
    - A la date t=T un système permet d'annuler la tension aux bornes du générateur. Par une étude analogue trouvée l'expression de la tension aux bornes du condensateur en fonction du temps pour t >=T.
    - Calculer la valeur maximale atteinte par la tension aux bornes du condensateur pendant l'intervalle de temps 0<t <2T d'une part pour T= 1    ms et d'autre part pour T= 10 ms.
  2. Dans le montage ci-dessus on remplace le générateur de tension constante par un générateur basse fréquence de tension sinusoïdale u(t) = Umcos( wt).
    - On admet que la tension aux bornes du condensateur est UC= A cos(    wt) + B sin(wt). Déterminer A et B en fonction de Um, R, C et w.
    Rappel : A cos(    wt) + B sin(wt) = (A²+B²)½cos( wt+j)
    - En déduire la valeur maximale UCmax de la tension aux bornes du condensateur en fonction de ces mêmes paramètres.
    - Les valeurs de R et C étant inchangées, déterminer les fréquences possibles de la tension du générateur pour lesquelles UCmax /Um <1/(racine carrée (2))
    - Le montage proposé est appelé "filtre passe bas". Justifier cette appellation.
  3. Dans le montage précédent on ajoute une bobine d'inductance L=0,1 H et de résistance négligeable. La tension sinusoïdale aux bornes du générateur est toujours u(t) = Umcos( wt).
    - La tension aux bornes du condensateur s'écrit Uc= A cos(    wt) + B sin(wt). Déterminer A et B en fonction de Um, R, C , L et w.
    - En déduire la valeur maximale UCmax de la tension aux bornes du condensateur en fonction de ces mêmes paramètres.
corrigé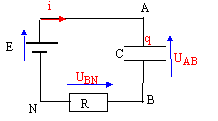

E = UAB + UBN ; E=UAB + R i avec i = dq/dt et q= C UAB soit i =C dUAB /dt

E = UAB +RCdUAB /dt

U= A(1-exp(Bt)) ; dU/dt = -A B exp(Bt)

repport dans l'équation différentielle : E= A(1-exp(Bt)) - RC A B exp(Bt)

E= A - Aexp(Bt)(1+RCB)

vérifiée si : 1+RCB = 0 soit B = -1/(RC) et si A= E.

A la date t=T, E s'annule ; la tension aux bornes du condensateur vaut U0 inférieure ou égale à E. On choisi cette date t comme nouvelle origine des dates.

Le condensateur chargé ( en partie ou complétement ) est en série avec un résistor : le condensateur se décharge à travers le résistor ; le courant de décharge a le sens contraire du courant de charge.

UAB+ UBN=0 ; UAB - R i = 0 avec i = -dq/dt et q = C UAB soit i = -C dUAB /dt

UAB +RC dUAB /dt =0

solution de cette équation différentielle : U=U0 exp( -t/(RC)).

T= 10-6 s ; RC= 220*10-6 =2,2 10-4 s. U0 = E(1-exp(-T/(RC)) = 5(1-exp(-10-6/2,2 10-4))= 2,3 10-2 V.

Le condensateur est très peu chargé puis il se décharge à travers le résistor : tension finale aux bornes du condensateur :

U=U0 exp( -T/(RC)) =2,3 10-2 exp(-10-6/2,2 10-4)) = 2,2 10-2 V .

T= 10-2 s ; U0 = E(1-exp(-T/(RC)) = 5(1-exp(-10-2/2,2 10-4))= 5 V.

Le condensateur est complétement chargé puis il se décharge à travers le résistor : tension finale aux bornes du condensateur :

U=U0 exp( -T/(RC)) =5 exp(-10-2/2,2 10-4)) = 0 V .

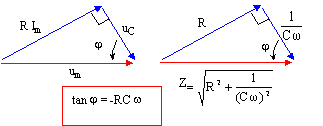
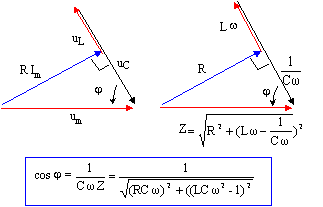
La tension aux bornes du condensateur est en retard de p/2 par rapport à l'intensité.

uCmax = um cos j avec cos j = 1/(Z Cw)= ( (RCw)²+1)-½.

uCmax =( (RCw)²+1)-½ um.

UCmax /um <1/(racine carrée (2)) ; ( (RCw)²+1)-½ <1/(racine carrée (2)) ; (RCw)²+1 >2 ;

RCw > 1 ; w > 1 /(RC)

or w = 2pf ; f >1 /(2pRC) ; f > 1 / (2*3,14*220 10-6) ; f > 724 Hz.

Les amplitudes des tensions de fréquence supérieures à 724 Hz sont plus petites que 0,707 um : ce dispositif , dont la tension de sortie est la tension aux bornes du condensateur, atténuent les fréquences élevées ; il ne laissent passer que les fréquences basses.

uCmax = Imax / Cw avec Imax = Umax/Z ; uCmax =Umax/ (ZCw )= Umax[(RCw)²+(LCw²-1)²]-½.


retour -menu