Deux éprouvettes graduées 1 et 2 contiennent respectivement 400 mL d'eau et 400 mL d'eau salée.
On dépose un oeuf de masse 57.0 grammes, de volume V(o) = 55 mL, à la surface de l'eau : il descend au fond de l'éprouvette 1. On le dépose ensuite à la surface de l'eau salée : il flotte à la surface de l'éprouvette 2. Le volume V(i) de sa partie immergée est 45 mL.
a) Quelle est la valeur de la masse volumique ro(S) de l'eau salée ?
b) Quelles sont les caractéristiques de la force R qu'exerce le fond de l'éprouvette 1 sur l'oeuf ?
(masse volumique de l'eau ro(eau)= 1000 kg/m3)

Dans l'eau salée, l'oeuf est soumis à deux forces opposées, même direction, sens contraire, même .
- le : vertical, vers le bas, valeur : mg = ro(o) V(o) g = mg = 0,057*9,8 = N
- la d'Archimède, verticale, vers le haut, valeur : poids du volume d'eau salée déplacé : ro(S) V(i) g
Ces forces ayant même valeur, on en déduit que : m= ro(S) V(i)
ro(S)= m/(V(i)= 57/ 45 = g/mL = kg/m3.
Dans l'eau, l'oeuf reposant au fond est en équilibre sous l'action de forces:
le poids, la poussée d'Archimède et la réaction du support ( le fond) : verticale, vers le haut, valeur : R= poids - poussée
R= mg- ro(eau)V(o)g= g(m-ro(eau)V(o))
masse en ; volume en ; masse volumique en soit ro(eau)=1kg/L
R= 9,8(0,057-0,055*1)=9,8*0,002 = .
-----------------------------------------------------------------------------------------------------------------------------------------------------------------
On considère une sphère de volume V = 1 m3 constitué d'un matériau de masse volumique "ro". La boué est complétement immergé et immobile, et lesté par une chaine de masse m=200 kg. On néglige la poussée d'archimède sur la chaine. La masse volumique de l'eau est égale à 1000 kg/m3.
1) Faire un schéma de la sphère en précisant les forces qui s'exercent sur elle.
2) Calculer la masse volumique (ro)
3) Que se passerait-il si la chaine se détachait ?
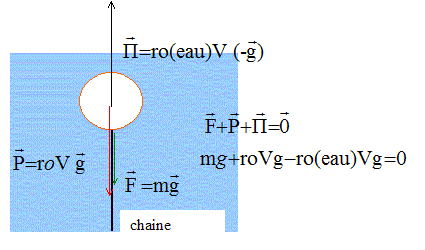
la sphère est en équilibre sous l'action de :
- son : verticale, vers le bas, valeur : P=ro V g
- la d'Archimède : verticale, vers le haut , valeur : ro(eau) V g
- du poids de la chaine, verticale, vers le bas, valeur F=mg
ro V+ m - ro(eau) V =0
soit ro = ro(eau -m/V
masse volumique en ; masse en , volume en .
ro = 1000-200/1 = 800 kg/m3.
La poussée d'Archimède vaut : 1000*1*9,8 = 9800 N.
Le poids de la sphère vaut : 800*1*9,8 = 7840 N
La poussée d'Archimède est au poids de la sphère : donc, si la chaine casse, la sphère va remonter en surface avec quand même une partie immergée.