Marie maintient immobile sous l'eau un glaçon cubique de côté a = 3,0 cm.
a) Représenter les forces qui s'exercent sur le glaçon.
b) Le glaçon est laché.
Calculer, à cet instant, les valeurs du poids du glaçon et de la poussée d'Archimède exercée sur le glaçon.
Représenter les forces qui s'exercent sur le glaçon. Que fait ce dernier ?
Masse volumique de l'eau : 1,0 g/mL Masse volumique de la glace : 0,9 g/mL
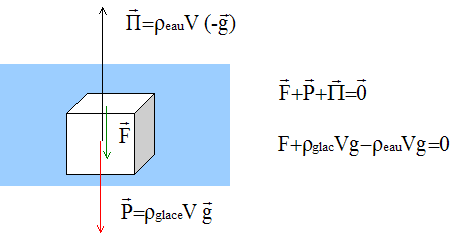
Le glaçon est soumis à son , à la poussée d'Archimède exercée par l', et à la force exercée par l'opérateur.
On lâche le glaçon : il reste soumis à son poids et à la poussée d'Archimède.
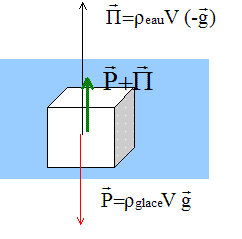
volume de la glace V= coté du glaçon au cube =3*3*3 = 27 centimètres cube
masse de la glace (g) = (centimètre cube) * masse volumique de la ( g/mL) = 27*0,9 = 24.3 g
mettre la masse en kilogramme :24.3 10 exposant kg.
Poids de la glace : P= m g =24.3 10 exposant -3 * 9,8 = 0,238 N
Poussée d'Archimède = poids du volume d'eau déplacé = 9,8 * volume de la glace * masse volumique de l'eau
masse d'eau déplacé (g) = volume glaçon (mL)*masse volumique eau ( g/mL) = 27*1=27g
mettre la masse en kg : 27 10 exposant-3 kg
Poussée = 27 10 exposant-3 * 9,8 = 0,265 N, valeur supérieure à celle du poids.
La somme de ces deux forces est donc verticale et dirigée vers le .
Sa valeur est voisine de : 0,265-0,238 = 0,027 N.
D"après la seconde loi de Newton, l' est verticale vers le haut et le glaçon remonte.

La vitesse de chute verticale d'un parachutiste de masse m = 100 kg se stabilise autour de 200 km/h, avant l'ouverture de son parachute.
a) Représenter les forces agissant sur le parachutiste ; la poussée d'Archimède due à l'air est négligeable. Donner leurs valeurs.
b) Pour des vitesses élevées, les forces de frottements exercés par l'air sont modélisées par une force unique, ayant la même direction que le vecteur vitesse, un sens opposé et sa valeur est proportionnelle au carré de la vitesse. Calculer la valeur du coefficient de proportionnalité, (coefficient de frottement ) noté k. g = 9,8 m/s²
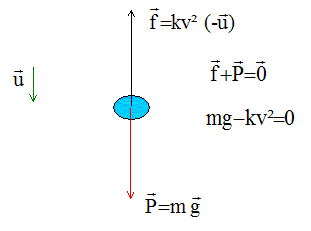
poids : vertical, vers le bas, P = mg =100*9,8 = 980 N
force de frottement avec l'air verticale vers le haut, valeur constante
Le mouvement est rectiligne : d'après la première loi de Newton, la somme vectorielle des forces est .
D'où et f = P = 980 N
Exprimer la vitesse en m/s : 200 / = 55,6 m/s
coefficient de frottement k= f/v² = 980/55,6² = 0,317