|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||
|
||
|
|
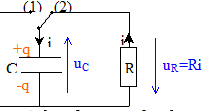
On veut vérifier la valeur de l'inductance indiquée par le curseur du dispositif de réglage d'une bobine à noyau de fer doux. Pour cela on va procéder en deux étapes : Première étape : on détermine la valeur de la capacité d'un condensateur par l'étude expérimentale de sa décharge à travers un conducteur ohmique. Seconde étape: on étudie la décharge de ce condensateur à travers la bobine pour en déduire la valeur de son inductance. Détermination de la capacité d'un condensateur : Le circuit d'étude du condensateur est schématisé ci-dessous : 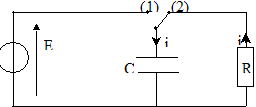
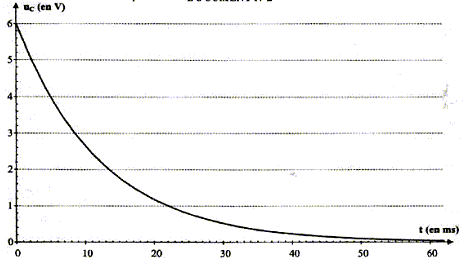
L'interrupteur est en position 1. Le condensateur est chargé sous la tension E. À la date t = 0, on commute l'interrupteur en position 2. Le condensateur se décharge à travers un conducteur ohmique de résistance R = 5,6 kW.
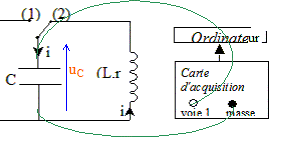
Mesure de l'inductance de la bobine : La bobine étudiée a une inductance L que l'on peut régler de 0,1 H à 1,1 H et une résistance r = 12 W. On admet que la relation uL = ri + Ldi/dt où uL et i sont définis en convention récepteur, reste valable aux bornes de la bobine avec noyau de fer doux. Pour mesurer une valeur L de l'inductance de la bobine, on place l'index de réglage sur 0,5 H. On réalise le circuit suivant :( C = 2,2 µF ). 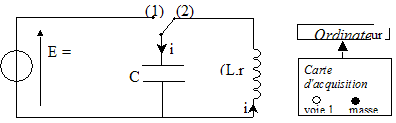 L'interrupteur est en position 1. Le condensateur est chargé sous la tension E. À la date t = 0, on commute l'interrupteur en position 2.
Bilan énergétique : Maintenant on s'intéresse à l'évolution temporelle des énergies emmagasinées par le condensateur et la bobine, WC et WL. 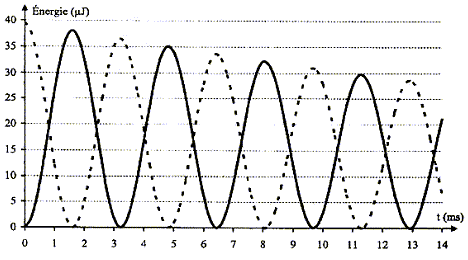
équation différentielle du circuit vérifiée par la tension uC :
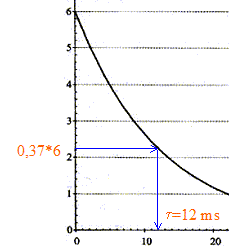
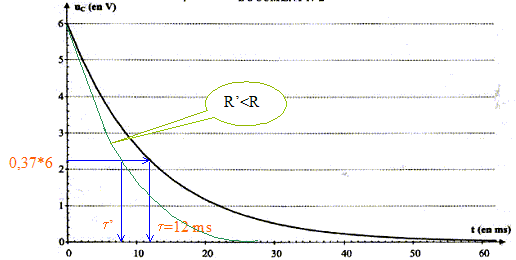
additivité des tensions : uC +uR=0 ; uC +Ri =0 ; d'une part i= dq/dt et d'autre part : q=CuC d'où i = CduC/dt par suite : uC + RC duC/dt= 0. La solution de l'équation différentielle est uC= E exp(-t/t). A t= 0 , la tension aux bornes du condensateur est-elle égale à uC(0)= E exp(0) = E. À t = t, la tension aux bornes du condensateur est-elle égale à uC(t)= E exp(-t/t) = E exp(-1) = 0,37 E soit 37 % de sa valeur initiale. valeur de la constante de temps t :
valeur de la capacité C du condensateur : d'une part t = 1,2 10-2 s et R = 5,6 kW = 5,6 103 W et d'autre part t =RC soit C= t /R = 1,2 10-2 /5,6 103 = 2,1 10-6 F. Allure de la courbe de décharge uC = f(t) dans le cas où on utilise un conducteur ohmique de résistance R' plus : d'une part t '= R'C et d'autre part R' est inférieure à R ; en conséquence t '<t
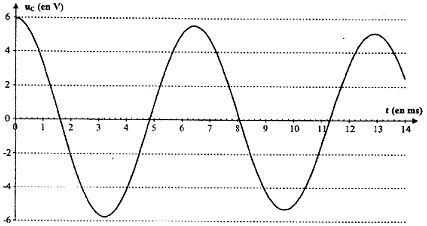
visualiser à l'ordinateur la tension uC aux bornes du condensateur :
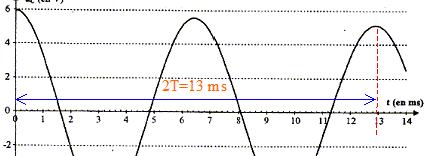
Le régime de la tension uC est pseudo-périodique car l'amplitude des oscillations diminue au cours du temps. valeur de l'inductance L du circuit :
D'une part T=T0= 6,5 10-3 s et d'autre part T0 = 2p(LC)½ soit T²0=4p² LC d'où L= T²0/(4p² C) avec C= 2,2 10-6 F ; L= (6,5 10-3)² / (4*3,14² *2,2 10-6 ) =0,487 soit 0,49 H. L'écart relatif vaut alors : (0,50-0,487) / 0,50 = 0,026 ( 2,6 %). L'indication de l'index est satisfaisante à 3% près. expressions des énergies WC et WL : L'énergie stockée par le condensateur s'exprime par : WC= ½CuC². L'énergie emmagasinée par la bobine s'exprime par : WL= ½Li². Les conditions initiales sont : condensateur chargé , uC= E ; intensité nulle. La courbe correspondant à WC ( courbe tracée en pointillés) présente donc une valeur maximale à l'instant initial, et la courbe correspondant à WL ( courbe en trait plein) passe par zéro à l'instant initial. En comparant les évolutions temporelles des énergies WC et WL, on constate que quand WC décroît alors WL croît et vis versa : il y a donc un échange permanent d'énergie entre condensateur et bobine. Au cours de cet échange, une partie de l'énergie est perdue, dissipée sous forme d'effet joule dans les parties résistives du circuit. L'énergie totale W = WC + WL emmagasinée par le circuit décroît donc au cours du temps. En associant en série avec la bobine à inductance réglable et le condensateur, un dipôle qui entretient les oscillations électriques, on compense à chaque instant l'énergie perdue par effet joule.
|
|
| |
||
|
|