|
La
radioactivité au service de l'archéologie,
céramiques et ultrasons , corrosion des gouttières d'après bac S France
2006
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.
|
|
|
|
La
radioactivité au service de l'archéologie ( 5,5 points)
Isotope radioactif du carbone, le "carbone 14" noté 14C
est formé continuellement dans la haute atmosphère. Il est très réactif
et donne rapidement du "gaz carbonique" (dioxyde de carbone) qui, en
quelques mois, se mélange avec l'ensemble du gaz carbonique de notre
atmosphère. Il sera donc assimilé par les plantes au même titre que le
gaz carbonique produit avec du carbone stable (les isotopes 12C
et 13C ). On le retrouvera donc comme constituant de la
matière organique des animaux herbivores et carnivores. [...]
Vers 1950, le chimiste américain W. Libby a démontré [...] que
tous les êtres vivants sont caractérisés par le même rapport du nombre
de noyaux de 14C au nombre de noyaux de 12C : N(14C)
/ (12C).
En conséquence, un gramme de carbone pur extrait d'un être
vivant présente une activité due au 14C, voisine de 13,6
désintégrations par minute, ce qui correspond à "un âge zéro". Dans un
animal ou un végétal mort (tronc d'arbre, coquille fossile, os...
trouvé dans une caverne), le 14C "assimilé" par l'animal ou
la plante quand il était vivant, décroît exponentiellement en fonction
du temps du fait de sa radioactivité à partir de l'instant de sa mort.
La comparaison(1) de cette activité résiduelle aux 13,6 désintégrations
par minute fournit directement l'âge de l'échantillon fossile [...]. Au
bout de 40 millénaires, iI reste moins de 1% du 14C que
contenait initialement un échantillon fossile ; cette teneur résiduelle
devient trop faible pour être déterminée avec précision.
J.C Duplessy et C. Laj ; D'après une publication du CEA ;
Clefs CEA n°14 automne 1989
(1) : On suppose que la valeur 13,6 désintégrations par
minute, pour un organisme vivant, est restée constante au cours des
derniers millénaires.
- Désintégration du "carbone 14"
On donne les numéros atomiques suivants : Z = 6 pour le carbone (C) et
Z = 7 pour l'azote (N).
- Pourquoi les noyaux de symboles 146C et 126C
sont-ils appelés isotopes ?
- Donner la composition du noyau de symbole 146C.
- Le "carbone 14" se désintègre "en azote 14". Ecrire l'équation de
désintégration du "carbone 14" en supposant que le noyau fils n'est pas
obtenu dans un état excité. S'agit-il d'une radioactivité a, b-, b + ?
- Propriétés des désintégrations radioactives
- Donner les caractéristiques des transformations radioactives en
complétant les phrases du cadre ci-dessous à l'aide des mots ou
expressions proposés.
|
La transformation radioactive d'un noyau possède un
caractère
|
|
Mots proposés
|
prévisible
|
aléatoire
|
périodique
|
|
La désintégration d'un noyau... celle d'un noyau
voisin
|
|
Expressions proposées
|
n'affecte pas
|
modifie
|
est perturbée par
|
|
Un noyau "âgé" a... de se désintégrer qu'un noyau
"jeune".
|
|
Expressions proposées :
|
plus de chances
|
moins de chances
|
autant de chances
|
|
L'évolution d'une population d'un grand nombre de
noyaux radioactifs possède un caractère...
|
|
Mots proposés
|
prévisible
|
aléatoire
|
périodique
|
- On propose trois expressions mathématiques pour représenter
l'évolution du nombre N de noyaux de "carbone 14" restant dans
l'échantillon à la date t, l étant la
constante radioactive relative à la désintégration étudiée (l > 0) :
(a) N = N0.e(-lt) ;
(b) N = N0-lt ; (c) N = N0.e(lt)
- Dans chacune des trois expressions ci-dessus : Que vaut N à t = 0 ?
Quelle est la limite de N quand t tend vers l'infini ? En déduire
l'expression à retenir parmi les propositions (a), (b) et (c), en
justifiant.
-L'activité à l'instant de date t est donnée par la relation A = A0.e(-lt). Que représente A0 ? En s'aidant
du texte, donner pour un échantillon de 1,0 g de carbone pur, extrait
d'un être vivant, la valeur de A0. A quel événement
correspond "l'âge zéro" cité dans le texte ?
- 3. Datation au "carbone 14"
Le temps de demi-vie de l'isotope est t1/2
=5,73 103 ans.
- Qu'appelle-t-on temps de demi-vie t1/2 d'un échantillon
radioactif ?
- Montrer que lt1/2=ln2.
-Calculer la valeur de l dans le cas du
"carbone 14", en gardant t1/2 en années.
- Plusieurs articles scientifiques parus en 2004 relatent les
informations apportées par la découverte d'Otzi, un homme naturellement
momifié par la glace et découvert, par des randonneurs, en septembre
1991 dans les Alpes italiennes. Pour dater le corps momifié, on a
mesuré l'activité d'un échantillon de la momie. On a trouvé une
activité égale à 7,16 désintégrations par minute pour une masse
équivalente à 1,0 g de carbone pur. Donner l'expression littérale de la
durée écoulée entre la mort d'Otzi et la mesure de l'activité de
l'échantillon. Calculer cette durée.
-A Obock (en République de Djibouti), des chercheurs ont étudié un
corail vieux de 1,2 105 ans (soit cent vingt mille ans).
D'après le texte, ce corail a-t-il pu être daté par la méthode
utilisant le "carbone 14" ? Justifier la réponse.
- Choix du radioélément
- Pour dater des roches très anciennes, on utilise parfois
la méthode potassium-argon. Le "potassium 40", de demi-vie 1,3 109
ans, se transforme en "argon 40". Quel pourcentage de noyaux de
"potassium 40" reste-t-il dans une roche au bout de 4 fois le temps de
demi-vie ?
- Comme il est indiqué dans le texte pour le "carbone 14", on suppose
que la teneur résiduelle minimale permettant d'effectuer une datation
avec le "potassium 40" est également de 1 % de la teneur initiale. En
comparant l'âge de la Terre, qui est de 4.5 109 ans, à la
demi-vie du "potassium 40", préciser si la méthode de datation par le
"potassium 40" permet de mesurer l'âge de la Terre. Justifier la
réponse.
corrigé
Les noyaux de symboles
146C et 126C sont
appelés isotopes :
ils ne différent que par leur nombre de neutrons,
respectivement 14-6=8 et 12-6 = 6 ; ils possèdent le même n° atomique (
ou nombre de charge Z=6).
composition du noyau de symbole 146C
: 6 protons et 14-6 = 8 neutrons.
équation de désintégration du "carbone 14" :
146C = 147N + AZX
conservation de la charge : 6=Z+7 soit Z= -1
conservation du nombre de nucléons : 14 = A+14 soit A= 0.
émission d'un électron 0-1e donc
radioactivité de type b-.
|
La transformation radioactive d'un noyau possède un
caractère
|
|
Mots proposés
|
prévisible
|
aléatoire
|
périodique
|
|
La désintégration d'un noyau... celle d'un noyau voisin
|
|
Expressions proposées
|
n'affecte pas
|
modifie
|
est perturbée par
|
|
Un noyau "âgé" a... de se désintégrer qu'un noyau
"jeune".
|
|
Expressions proposées :
|
plus de chances
|
moins de chances
|
autant de chances
|
|
L'évolution d'une population d'un grand nombre de noyaux
radioactifs possède un caractère...
|
|
Mots proposés
|
prévisible
|
aléatoire
|
périodique
|
La bonne expression :
(a) N = N0exp(-lt)
; (b) N = N0-lt ; (c) N = N0.e(lt)
à t=0 , N=N0, nombre de noyaux initiaux
quand t tend vers l'infini , tous les noyaux se sont
désintégrés et, en conséquence la limite de N est zéro: ce qui exclut
les expressions b et c.
L'activité A = A0.exp(-lt).
A0 : activité initiale à la date choisie comme
origine des temps.
pour un échantillon de 1,0 g decarbone pur, extrait d'un être
vivant, la valeur de A0 est, d'après le texte : A0
= 13,6 désintégrations/min ou 13,6/60 =0,227 Bq
"l'âge zéro" cité dans le texte correspond à l'événement :
mort de l'être vivant.
temps de demi-vie t1/2
d'un échantillon radioactif :
(ou période) notée t½, d'un échantillon de noyaux radioactifs
est égale à la durée au bout de laquelle la moitié des noyaux
radioactifs initiaux se sont désintègrés.
à t = t½, A(t½) = ½A0 = A0
exp (-lt½) ; 0,5 = exp (-lt½) ; ln 0,5 = -lt½ ; ln2 = lt½
dans le cas du carbone 14 : l= ln2/t½ =
0,69 / 5,73 103 =1,21 10-4 an-1.
expression littérale de la durée écoulée entre la mort
d'Otzi et la mesure de l'activité de l'échantillon :
A = A0.exp(-lt) ; A / A0=
exp(-lt) ; ln(A / A0) = -lt ; ln(A0 / A) = lt
; t = ln(A0 / A) / l.
t= ln(13,6/7,16) / (1,21 10-4 )= 5,30 104 années.
Datation du corail :
"Au bout de 40 millénaires, iI reste moins de 1% du 14C
que contenait initialement un échantillon fossile ; cette teneur
résiduelle devient trop faible pour être déterminée avec précision"
120 000 ans est bien supérieur à 40 000 ans ; en conséquence
ce corail ne contient pratiquement plus de carbone 14 ; cette teneur
résiduelle ne permet pas une datation précise.
la méthode potassium-argon
:
pourcentage de noyaux de "potassium 40" restant dans une roche
au bout de 4 fois le temps de demi-vie :
à t=t½, il en reste 50% ; à t=2t½, il en
reste 25% ; à t=3t½, il en reste 12,5% ; à t=4t½,
il en reste 6,25% ;( soit 2-4)
âge de la Terre, qui est de 4,5 109 ans ; temps de demi-vie
du "potassium 40" t½=1,3 109 ans ;
l'âge de la terre correspond à 4,5 109 /1,3 109
= 4,5/1,3 = 3,461 temps de demi- vie du potassium 40.
Il reste donc : 2-3,461 = 0,091 ( 9,10 %) de
potassium 40, valeur supérieure à 1%.
la méthode de datation par le "potassium 40" permet donc de
mesurer l'âge de la Terre.
|
|
Céramiques et ultrasons (4
points)
Les ultrasons sont utilisés dans de nombreux domaines de la
vie courante : échographie, détecteurs de présence dans les alarmes,
etc. Les émetteurs et les récepteurs d'ultrasons sont fréquemment
constitués de céramiques piézoélectriques.
Les parties 1 et 2 de cet exercice sont indépendantes.
- Emission et propagation de l'onde ultrasonore produite
par une céramique piézoélectrique :
Lorsqu'on applique une tension sinusoïdale d'amplitude suffisante et de
fréquence appropriée entre les deux faces métallisées et opposées d'une
céramique piézoélectrique, elle se met à vibrer. Lorsque la céramique
entre en résonance, elle émet des ultrasons. La fréquence des ultrasons
émis est égale à la fréquence de vibration de la céramique émettrice.
- Propagation des ondes ultrasonores :
On réalise le montage schématisé figure ci-dessous. Le
récepteur, constitué d'une céramique réceptrice, est placé à une
distance d, face à la céramique émettrice. Une tension de même
fréquence que les ultrasons reçus apparaît aux bornes de la céramique
réceptrice. On visualise cette tension sur la voie A d'un oscilloscope.
L'oscillogramme obtenu est représenté sur la figure ci-dessous. Le
coefficient de balayage est égal à 10 µs/div et la sensibilité
verticale à 0,2 V/div. On rappelle que la célérité des ultrasons dans
l'air est vair = 340 m.s-1 dans les conditions de
l'expérience.
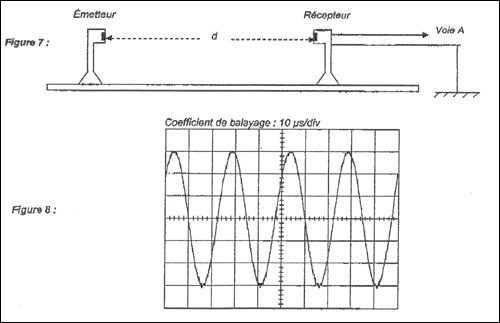
Déterminer la période T et la fréquence f de la tension
observée à l'oscilloscope. En déduire la fréquence f des
ultrasons. Justifier.
Donner l'expression littérale puis la valeur de la longueur d'onde l des ultrasons dans l'air.
- Résonance de la céramique émettrice :
Pour une valeur appropriée de la fréquence de la tension
sinusoïdale appliquée, son amplitude restant constante, la céramique
émettrice entre en résonance. La tension sinusoïdale joue alors le rôle
d'un excitateur et la céramique celui d'un résonateur. Que peut-on dire
de la valeur de la fréquence de la tension excitatrice à la résonance ?
Décrire qualitativement le phénomène de résonance en ce qui concerne
l'amplitude de vibration de la céramique.
- Oscillations libres dans un circuit RCL série :
Pour étudier les conditions d'obtention d'oscillations
électriques libres à la fréquence propre f0 = 40 kHz, on
réalise le circuit schématisé figure ci-dessous. Un oscilloscope à
mémoire permet d'enregistrer la tension aux bornes du condensateur.
L'oscillogramme est représenté sur la figure ci-dessous. La bobine a
une inductance de valeur L = 1,0 mH ; R est la résistance totale du
circuit. Le condensateur est initialement chargé sous une tension Uc
= 4,0 V. A l'instant de date t = 0 s, on ferme l'interrupteur K.
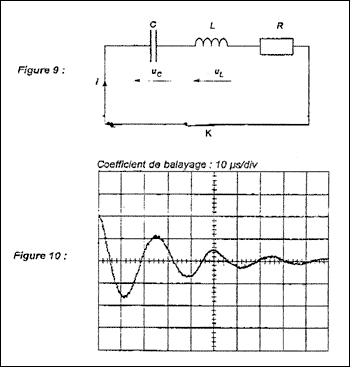
Comment appelle-t-on le type de régime correspondant à la
figure ci-dessus ?
Interpréter en termes d'énergie l'amortissement des oscillations, que
l'on observe.
Comment peut-on éviter l'amortissement des oscillations, sachant que la
résistance du circuit ne peut être nulle ?
Dire si les affirmations ci-dessous concernant les oscillations libres
d'un dipôle RLC sont vraies ou fausse. Commentez brièvement.
Affirmation 1 : En augmentant la résistance R d'un dipôle
RLC on observera toujours des oscillations amorties.
Affirmation 2 : la valeur de la période propre d'un dipôle
RLC dépend de la charge initiale du condensateur.
- Détermination de la capacité d'un condensateur :
Dans le cas étudié, l'amortissement est assez faible pour
pouvoir confondre la pseudo période du dipôle RLC avec la période
propre T0 du dipôle LC (L et C ayant les mêmes valeurs
respectives dans les deux cas). On considère le circuit LC représenté à
la figure ci-dessous.L'interrupteur K est ouvert et la tension aux
bornes du condensateur est égale à U0. A l'instant de date t
= 0 s, on ferme l'interrupteur K. Après avoir établi l'expression de
l'intensité i du courant en fonction de la tension uc
montrer que l'équation différentielle vérifiée par la tension uc(t)
aux bornes du condensateur est: d²uc/dt + 1/(LC) uc
= 0
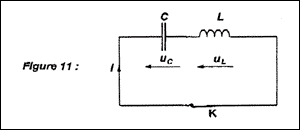
- La solution de cette équation différentielle peut
s'écrire uc(t) = U0cos(2pt/T0).
En déduire, en utilisant l'équation différentielle, l'expression
littérale de la période propre T0 du circuit.
Calculer la valeur à donner à la capacité C du condensateur de manière
à obtenir des oscillations à la fréquence f0 = 40 kHz.
corrigé
période T et fréquence f
de la tension observée à l'oscilloscope :
deux périodes correspondent à 5 divisions soit 50 ms; T= 25ms = 2,5 10-5 s.
fréquence f = 1/T = 105/2,5 = 4,0 104 Hz
= 40 kHz.
fréquence f des ultrasons = fréquence du
signal observé à l'oscilloscope = 40 kHz
" Une tension de même fréquence que les ultrasons reçus
apparaît aux bornes de la céramique réceptrice"
expression littérale et la valeur de la longueur d'onde l des ultrasons dans l'air :
l = c /f = 340/4 104 = 8,5 10-3 m.
Résonance de la céramique
émettrice :
à la résonance la valeur de la fréquence de la tension
excitatrice est égale à la fréquence propre du résonateur.
Description du phénomène de résonance en ce qui
concerne l'amplitude de vibration de la céramique :
la céramique est soumise à des oscillations forcées ; à la
résonance l'amplitude des oscillations devient très grande alors que
pour des fréquences excitatrices très différentes de la fréquence
propre de la séramique, l'amplitude des oscillations restet faible.
Oscillations libres dans
un circuit RCL série :
-
type de régime correspondant à la figure :
oscillations libres pseudo-périodiques.
Interpréation en termes d'énergie de
l'amortissement des oscillations :
au cours des échanges d'énergie entre condensateur et
bobine, une partie de l'énergie est dissipée sous forme de chaleur (
effet joule) dans les résistances ( conducteur ohmique)
-
On éviter l'amortissement des oscillations en
compensant à chaque instant l'énergie perdue ( par exemple à l'aide
d'un dispositif électronique simulant une résistance négative)
L'affirmation 1 est fausse : "En augmentant la
résistance R d'un dipôle RLC on observera toujours des oscillations
amorties".
Aumgmenter R c'est augmenter l'énergie dissipée sous
forme d'effet joule ; les oscillations s'amortissent de plus en plus :
on aboutit à un régime apériodique.
L'affirmation 2 est fausse : "la valeur de la
période propre d'un dipôle RLC dépend de la charge initiale du
condensateur".
La pseudo-période ( si amortissement faible) dépend de
l'inductance de la bobine et de la capacité du condensateur T=2p(LC)½.
Détermination de la
capacité d'un condensateur :
équation différentielle vérifiée par la tension uc(t)
aux bornes du condensateur
tension aux bornes du condensateur : uc(t) ; avec
q(t) = C uc(t) et i (t) =q(t) /dt = Cd uc(t)/dt ;
di(t)/dt = Cd²uc(t)/dt²
tension aux bornes de la bobine : uL(t) = Ldi(t)/dt
= LCd²uc(t)/dt²
additivité des tensions : uc(t) +uL(t)
=0 ; uc(t)+ LCd²uc(t)/dt² =0
soit : d²uc/dt + 1/(LC) uc
= 0
solution de cette équation différentielle : uc(t) =
U0cos(2pt/T0).
expression littérale de la période propre T0
du circuit :
dériver deux fois uc(t) = U0cos(2pt/T0) par rapport au temps :
u'c(t) = -U02p/T0sin(2pt/T0) ; u"c(t) = -U0(2p/T0)2cos(2pt/T0) = - (2p/T0)2uc(t)
repport dans l'équation différentielle : - (2p/T0)2uc(t) +
1/(LC)uc(t) =0
cela est vérifié quel que soit t si : (2p/T0)2
= 1/(LC) soit T0 = 2p(LC)½.
valeur de la capacité C du condensateur de manière à
obtenir des oscillations à la fréquence f0 = 40 kHz :
T0 = 2,5 10-5 s ; C= T²0/(4p²L) = 2,5² 10-10/(4p²10-3) =1,6 10-8 F = 16 nF.
|
|
Corrosion des gouttières
Les précipitations sont naturellement acides en raison du
dioxyde de carbone présent dans l'atmosphère. Par ailleurs, la
combustion des matières fossiles (charbon, pétrole et gaz) produit du
dioxyde de soufre et des oxydes d'azote qui s'associent à l'humidité de
l'air pour libérer de l'acide sulfurique et de l'acide nitrique. Ces
acides sont ensuite transportés loin de leur source avant d'être
précipités par les pluies, le brouillard, la neige ou sous forme de
dépôts secs.
Très souvent, les pluies s'écoulant des toits sont recueillies
par des gouttières métalliques constituées de zinc.
Données : Masse molaire atomique du zinc : M(Zn) = 65,4
g.mol ; loi des gaz parfaits : PV = nRT
Couples acide/base : H3O+/H2O
(l) ; H2O (l)/HO- (aq) ; CO2, H2O
(l)/HCO3-(aq)
Le zinc est un métal qui réagit en milieu acide selon la
réaction d'équation : Zn (s) + 2 H3O+ = Zn2+
(aq) + H2 (g) + 2 H2O (l)
- Suivi cinétique de la transformation :
Pour étudier cette transformation, considérée comme
totale, on réalise l'expérience dont le schéma simplifié est représenté
sur la figure 1.
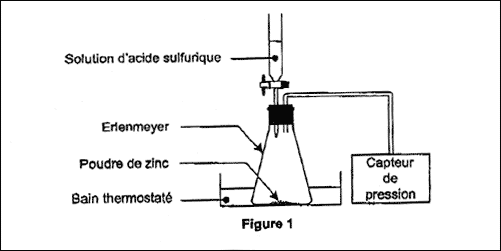
A l'instant de date t = 0 s, on verse rapidement, sur 0,50
g de poudre de zinc, 75,0 mL de solution d'acide sulfurique de
concentration en ions oxonium H3O+ égale à 0,40
mol.L-1. La pression mesurée à cet instant par le capteur
est Pi = 1020 hPa. La formation de dihydrogène crée une
surpression qui s'additionne à la pression de l'air initialement
présent. Les valeurs de la pression, mesurée à différentes dates par le
capteur de pression, sont reportées dans le tableau suivant :
|
t(min)
|
0
|
1,0
|
3,0
|
5,0
|
7,0
|
9,0
|
11,0
|
15,0
|
20,0
|
25,0
|
30,0
|
35,0
|
|
P(hPa)
|
1020
|
1030
|
1060
|
1082
|
1101
|
1120
|
1138
|
1172
|
1215
|
1259
|
1296
|
1335
|
|
t(min)
|
45,0
|
50,0
|
60,0
|
70,0
|
80,0
|
90,0
|
110,0
|
140,0
|
160,0
|
190,0
|
240,0
|
300,0
|
|
P(hPa)
|
1413
|
1452
|
1513
|
1565
|
1608
|
1641
|
1697
|
1744
|
1749
|
1757
|
1757
|
1757
|
- Etablir le tableau d'évolution du système.
- En déduire la valeur de l'avancement maximal xmax. Quel
est le réactif limitant ?
- On considère que le dihydrogène libéré par la réaction est un gaz
parfait. A chaque instant la surpression (P — Pi) est
proportionnelle à la quantité n(H2) de dihydrogène formé et
inversement proportionnelle au volume Vgaz de gaz contenu
dans l'erlenmeyer : (P — Pi) Vgaz = n(H2)
RT, où Pi représente la pression mesurée à la date t = 0 s,
P la pression mesurée par le capteur et T la température du milieu
(maintenue constante pendant l'expérience).Quelle est la relation
donnant l'avancement x de la réaction en fonction de (P — Pi),
Vgaz, R et T ?
On note Pmax la pression mesurée à l'état final. Ecrire la
relation donnant l'avancement xmax en fonction de Pmax, Pi,
Vgaz, R et T. En déduire la relation donnant l'avancement x
=xmax(P — Pi)/(Pmax — Pi).
La courbe donnant l'évolution de l'avancement x en fonction du temps
est représentée sur la figure 2 ci-dessous. Vérifier à l'aide de la
courbe la valeur de xmax trouvée précédemment.
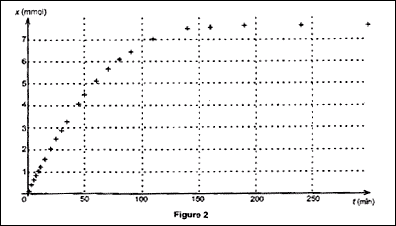
A l'aide du tableau des résultats, déterminer la valeur de
l'avancement à la date t = 50,0 min. Vérifier cette valeur sur la
courbe.
Comment peut-on déduire de la figure 2 l'évolution de la vitesse
volumique de réaction au cours de la transformation chimique étudiée ?
Décrire qualitativement cette évolution.
- Facteurs cinétiques :
2.1. Influence de la concentration en ions oxonium
On reprend le montage précédent (figure 1) et on réalise
les trois expériences suivantes :
|
expérience 1
|
expérience 2
|
expérience 3
|
|
température (°C)
|
25
|
25
|
25
|
|
masse initiale de zinc en poudre
|
0,50 g
|
0,50 g
|
0,50 g
|
|
volume acide sulfurique versé (mL)
|
75
|
75
|
75
|
|
concentration initiale en ion oxonium (mol/L)
|
0,50
|
0,25
|
0,40
|
Pour chacune des expériences 1, 2 et 3, on a tracé sur la figure 3
ci-dessous les trois courbes (a), (b) et (c) représentant l'avancement
de la réaction lors des 50 premières minutes.
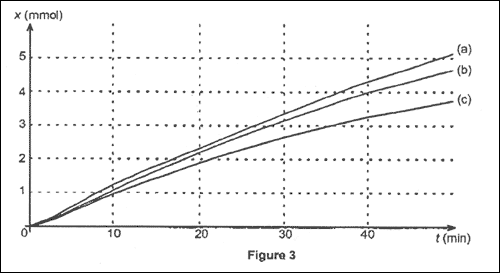
Associer à chacune des courbes de la figure 3 le numéro de
l'expérience 1, 2 ou 3 correspondante. Justifier.
- Influence de la forme du zinc (division et état de surface) :
On reprend le montage de la figure 1 et on réalise trois nouvelles
expériences : avec de la poudre de zinc ; avec de la grenaille de zinc
récemment fabriquée ; avec de la grenaille de zinc de fabrication
ancienne.
|
expérience4
|
expérience5
|
expérience 6
|
|
température (°C)
|
25
|
25
|
25
|
|
masse initiale de zinc (g)
|
0,50
|
0,50
|
0,50
|
|
forme du zinc
|
poudre
|
grenaille
|
grenaille de sinc fabrication ancienne
recouverte d'une couche de carbonate de zinc
|
|
Volume de la solution d'acide sulfurique versé
(mL
|
75
|
75
|
75
|
|
Concentration initiale en ions oxonium (mol/L)
|
0,50
|
0,50
|
0,50
|
On trace les courbes × = f(t) pour les trois expériences et on obtient
la figure 4 ci-dessous :
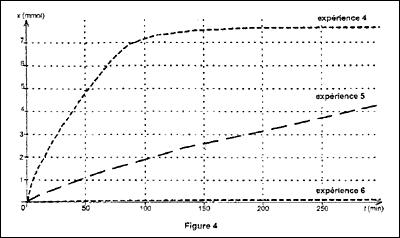
A partir des courbes obtenues lors des expériences 4 et 5,
indiquer quelle est l'influence de la surface du zinc en contact avec
la solution sur la vitesse de réaction.
En milieu humide, le zinc se couvre d'une mince couche de carbonate de
zinc qui lui donne un aspect patine. A partir des courbes obtenues,
indiquer quelle est l'influence de cette couche de carbonate de zinc
sur la vitesse de réaction.
- Pluies acides et gouttières :
Les précipitations naturelles et non polluées ont un pH
acide. Leur acidité est due au dioxyde de carbone qui se dissout dans
l'eau.
L'équation entre l'eau et le dioxyde de carbone s'écrit :
CO2 (aq) + 2H2O (l) = HCO3-(aq)
+ H3O+.
En France le pH moyen annuel des eaux de pluie est de
l'ordre de 5. A partir de la valeur du pH citée, déterminer la valeur
moyenne de la concentration en ions oxonium H3O+
rencontrés dans les eaux de pluie.
Les trois facteurs cinétiques étudiés dans la question 2.
permettent-ils d'expliquer la longévité des gouttières en zinc dans les
habitations ?
corrigé
Suivi cinétique de la
transformation :
Quantités de matière initiales :
Zinc : n(Zn) = m(g) / M(Zn) = 0,50 / 65,4 = 7,6 10-3
mol
ion oxonium : n(H3O+)= volume solution
(L) * concentration (mol/L) = 0,075*0,4 = 3,0 10-2 mol
|
avancement (mol)
|
Zn (s)
|
+ 2 H3O+
|
= Zn2+ (aq)
|
+ H2 (g)
|
+ 2 H2O (l)
|
|
initial
|
0
|
7,6 10-3
|
3,0 10-2
|
0
|
0
|
solvant en grand excès
|
|
en cours
|
x
|
7,6 10-3-x
|
3,0 10-2-2x
|
x
|
x
|
|
fin
|
xmax
|
7,6 10-3-xmax
|
3,0 10-2-2xmax
|
xmax
|
xmax
|
si le zinc est en excès : 7,6 10-3-xmax = 0 soit xmax
=7,6 10-3 mol
si l'acide est en excès : 3,0 10-2-2xmax
= 0 soit xmax =1,5 10-2 mol
on retient la plus petite valeur : xmax =7,6 10-3
mol ( zinc en défaut)
La courbe x(mmol) = f(t) tend vesre une valeur limite (
asymptote horizontale ) égale à 7,6 mmol
relation donnant l'avancement x de la réaction en fonction de
(P — Pi), Vgaz, R et T :
loi des gaz parfaitx : (P — Pi) Vgaz =
n(H2) RT
le tableau d'avancement indique : x= n(H2) d'où :
(P — Pi) Vgaz = x RT (1)
relation donnant l'avancement xmax en fonction de Pmax,
Pi, Vgaz, R et T : (Pmax — Pi)
Vgaz = xmax RT (2)
diviser (1) par (2) : (P — Pi) / (Pmax — Pi)
= x/ xmax
soit x =xmax(P — Pi)/(Pmax — Pi).
valeur de l'avancement à la date t = 50,0 min : P= 1452
hPa ; Pi= 1020 hPa ; Pmax = 1757 hPa.
x= xmax(P — Pi)/(Pmax — Pi)=
7,6(1452-1020) / ( 1757-1020) = 4,5 mmol.
cette valeur se retrouve sur la courbe.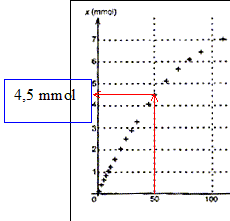
évolution de la vitesse volumique de réaction au cours
de la transformation chimique étudiée :
tracer les tangentes à diférentes dates à la courbe x= f(t) ;
les coefficients directeurs de ces tangentes donnent dx/dt ; diviser
par le volume V de la solution pour obtenir la vitesse v = 1/V dx/dt.
Les tangentes sont de plus en plus inclinées sur l'horizontale
au cours du temps ; les coeffidinet directeurs de ces droites diminuent
au cours du temps : la vitesse de la réaction diminue au cours du temps
( du fait de la diminution des quantités de matière des réactifs).
Zn (s) + 2 H3O+ = Zn2+ (aq) +
H2 (g) + 2 H2O (l)
Facteurs cinétiques :
à chacune des courbes de la figure 3 le numéro de
l'expérience 1, 2 ou 3 correspondante :
Pour les trois expériences, la température et la masse de zinc
sont identiques ; par contre les quantités de matière d'ion oxonium (
volume * concentration) sont différentes.
Or la concentration de l'ion oxonium, l'un des réactifs, est
un facteur cinétique : la vitesse, à une date donnée, est d'autant plus
grande que la concentration de cet ion est grande.
d'où l'assoaciation : ( courbe a : expérience 1) ; ( courbe b
: expérience 3) ;( courbe c : expérience 2) ;
Influence de la forme du zinc (division et état de
surface) :
influence de la surface du zinc en contact avec la solution
sur la vitesse de réaction :
poudre : grande surface de contact ( expérience 4) ; grenaille
: surface de contact plus faible que pour la poudre ( expérience 5)
à une date donnée, la vitesse est d'autant plus grande que la
surface du réactif solide est grande.
En milieu humide, le zinc se couvre d'une mince couche de carbonate de
zinc qui lui donne un aspect patine. ( expérience 6) : la vitesse de la
réaction est quasiment nulle ; le métal zinc est protégé d'une attaque
de l'acide par la couche "protectrice" de carbonate de zinc.
Pluies acides et gouttières
:
En France le pH moyen annuel des eaux de pluie est de l'ordre
de 5. La valeur moyenne de la concentration en ions oxonium H3O+
rencontrés dans les eaux de pluie est [H3O+]= 10-pH
= 10-5 mol/L.
Les trois facteurs cinétiques étudiés permettents d'expliquer la
longévité des gouttières en zinc dans les habitations :
en effet la concentration en ion oxonium est faible, le métal
est protégé par une couche de carbonate de zinc protectrice, le métal
présente une très faible surface de contact ( par rapport à une poudre)
avec les acides.
|
|
|
|
retour -menu
|








