|
Les données et les informations utilisées dans cet exercice
sont issues des sites internet du Réseau National de Surveilance
Sismique et de l'Ecole et Observatoire de la Terre :
http://renass.u.strasbg.fr ; http://eost.u.strasbg.fr.
Le 23 /02/2004 un séisme de magnitude 5,1 s'est produit à
Roulans, à 20 km au nord est de Besançon. Ce séisme a été ressenti dans
tout l'est de la France, en Suisse et dans le nord ouest de
l'Allemegne, sans faire de victimes, ni de dégats significatifs.
Lors d'un séisme, les ondes traversent la Terre. Elles se
succèdent et se superposent sur les enregistrements des sismomètres.
Leur vitesse et leur amplitude sont modifiées par les structures
géologiques traversées. C'est pourquoi les signaux enregistrés sont la
combinaison d'effets liés à la source, aux milieux traversés et aux
instruments de mesure.
Parmi les ondes sismiques on distingue :
- Les ondes P ou ondes primaires, qui sont des ondes de compression
longitudinales ; leur célérité vP vaut en moyenne 6,0 km/s.
- Les ondes S ou ondes secondaires, qui sont des ondes de
cisaillement ou ondes transversales ; leur célérité vS vaut
en moyenne 3,5 km/s.
Etude d'un sismographe :
- En utilisant les informations du texte ci-dessus, associer
à chaque signal observé sur le sismographe, le type d'onde détectées.
Justifier.
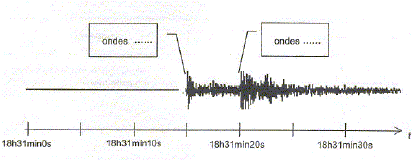
- Relever les dates d'arrivée des ondes S et P à la station
d'enregistrement notées respectivement tS et tP.
- Soit d la distance qui sépare la station d'enregistrement
du lieu où le séisme se produit. Exprimer la célérité notées vS
des ondes S en fonction de la distance d parcourue et des dates tS
et t0. Faire de même avec les ondes P avec les dates tP
et t0.
- Retrouver l'expression de d : d= vPvS/
(vP-vS) (tS-tP)
- En déduire la valeur numérique de d.
Fonctionnement du sismomètre
:
Un sismomètre est un appareil capable de détecter de très
petits mouvements du sol et de les enregistrer, par un procédé
anamogique ou numérique, en suivant une base de temps très précise. Il
fonctionne sur le même principe qu'un oscillateur solide-ressort amorti
fixé à un bâti fixe au sol. Les sismomètres sont sensibles aux
vibrations verticales ou horizontales du sol. On s'intéresse ici au
fonctionnement d'un sismomètre horizontal.
- Etude des oscillations libres en l'absence de tout séisme :
On modélise le sismomètre horizontal par un système ressort-solide. Le
ressort de constante de raideur k est fixé par une extrémité à un bâti
B. Le solide de masse m et de centre d'inertie G se déplace le long
d'un support rectiligne horizontal. La projection de G est repérée sur
l'axe Ox par son abscisse x(t).
L'origine O représente la projection du point G lorsque la longueur du
ressort correspond à sa longueur à vide. En l'absence de tout séisme,
on étudie les oscillations libres du système solide-ressort et on
néglige tout frottement.
Le bâti est alors supposé fixe dans le référentiel terrestre supposé
galiléen.
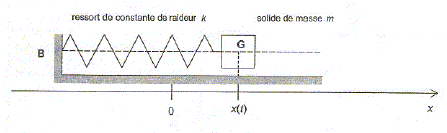
- Faire l'inventaire des forces extérieures exercées sur
le solide et les représentéer sur le schéma.
- Appliquer la seconde loi de Newton au centre d'inertie G du solide
pour établir l'équation différentielle vérifiée par x(t).
- La période propre T0 des oscillations libres du solide est
T0 = 2p(m/k)½.
Vérifier la cohérence de cette expression par une analyse
dimensionnelle.
- Etude des oscillations forcées lors du séisme :
Lors d'un séisme, le sismomètre fonctionne en oscillations
forcées. Le solide est en mouvement relatif par rapport au bâti. C'est
ce mouvement relatif qui est enregistré par un dispositif mécanique,
optique ou électronique. On admettra que pendant un séisme, le sol et
donc le bâti, ont un mouvement de vibration sinusoïdale.
- Quel est l'excitateur ? Quel est le résonateur ?
Il existe différentes classes de sismomètres en fonction
de la fréquence des ondes sinusoïdales qui composent le signal. En
effet, un signal sismique peut comporter des ondes dont les périodes
vont de quelques centièmes de seconde à plusieurs minutes. Le
sismomètre entre en résonance pour une fréquence particulière. Il
comporte également un système d'amortissement, nécessaire pour obtenir
une restitution fidèle du mouvement du sol.
- En admettant que l'amortissement est suffisamment
faible, pour quelle période de l'excitateur ce phénomène de résonance
se produit-il ?
- Pour simplifier le raisonnement on considère que les ondes S et P
sont périodiques. En analysant le premier document ci-dessus dire si
l'ordre de grandeur de la période des ondes P et S est plutôt de 10 s,
ou 1 s, ou 0,1 s. Justifier.
- A partir de l'expression de la période T0, calculer la
valeur approchée de la masse m du solide qui, dans le cas d'un
tremblement de Terre, a permis de relever le sismogramme des ondes P et
S. La constante de raideur du ressort est k=100 N/m. ( p² = 10)
- Certaines ondes se propageant lors d'un séisme sont de fréquences
beaucoup plus basses que celles des ondes P et S. Comment faudrait-il
modifier la masse m pour les enregistrer ?
A propos des séismes :
répondre aux questions en justifiant brièvement.
|
questions
|
réponses
|
|
A partir de l'épicentre, les ondes sismiques se
propagent-elles dans une direction privilégiée ?
|
|
|
Les ondes sismiques se propagent-elles avec
transport de matière ?
|
|
|
Définir une onde longitudinale.
|
|
|
Exprimer puis calculer la longueur d'onde l d'une onde P de période T=0,2 s.
|
|
|
Pourquoi le texte donne t-il les célérités moyennes
pour les célérités des ondes sismiques ?
|
|
-
corrigé
Etude d'un sismographe :
Les ondes de compression longitudinales ( célérité vP
=6,0 km/s) arrivent en premier au sismomètre.
Les ondes S ou ondes secondaires ( célérité vS =
3,5 km/s, valeur plus faible que vP) arrivent un peu plus
tard au sismomètre.
Dates d'arrivée des ondes S et P à la station
d'enregistrement notées respectivement tS et tP
:
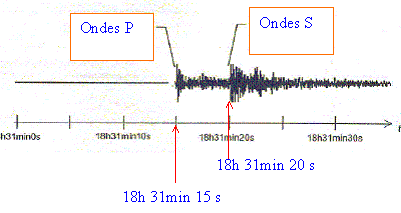
Soit d la distance qui sépare la station d'enregistrement du
lieu où le séisme se produit.
Expression de la célérité notée vS des
ondes S en fonction de la distance d parcourue et des dates tS
et t0.
vS= d / (tS - t0) soit t0
= tS +d/vS
Expression de la célérité notée vP des
ondes S en fonction de la distance d parcourue et des dates tP
et t0.
vP= d / (tP - t0) soit t0
= tP +d/vP
Expression de d : t0 = tS +d/vS
=tP +d/vP
tS -tP =d[1/vS - 1/vP]
= d(vP-vS) / (vPvS)
d= vPvS/ (vP-vS) (tS-tP)
valeur numérique de d : d = 6 103*3,5 103
*5/(6 103-3,5 103) = 6*3,5 *5 103 /2,5
= 42 103 m = 42 km.
Etude
des oscillations libres en l'absence de tout séisme :
-
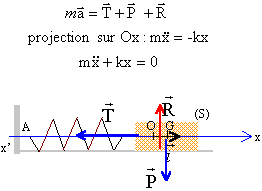
Inventaire des forces extérieures exercées sur le solide
:
poids, vertical, vers le bas, appliqué en G, valeur P=mg
action du support, verticale, vers le haut, valeur R=P.
tension du ressort, horizontale, dirigée vers O, valeur kx
La période propre T0 des oscillations libres du
solide est T0 = 2p(m/k)½.
Cohérence de cette expression par une analyse dimensionnelle
: [T0] = T ( a la dimension d'une durée notée T )
2p est sans dimension ; masse m (
kg) [m]= M
k raideur ( N/m) est une force divisée par une longueur ; une
force est une accélération fois une masse ; une accélération est une
distance divisée par le carré d'un temps :
[a]= LT-2 ; [force]= MLT-2 ; [k] = MT-2
;
par suite [(m/k)] = T2 ; [(m/k)½]= T
Etude
des oscillations forcées lors du séisme :
L'excitateur est le tremblement de terre provoquant des ondes
P et S.
Le résonateur est le solide masse-ressort horizontal.
En admettant que l'amortissement est suffisamment faible, ce phénomène
de résonance se produit lorsque la période de l'excitateur est égale à
la période propre T0 du résonateur.
Ordre de grandeur de la période des ondes P et S :
sur une durée de 5 s on décompte plusieurs dizaines de
périodes : donc la période est de l'ordre de 0,1 s.
Calcul de la valeur approchée de la masse m du solide :
k=100 N/m ; T0 = 0,1 s ;( p²
= 10)
T0 = 2p(m / k)½
; T20 = 4p²m/k ; m = T20
k / (4p²) = 0,01*100 / 40 =1/40 = 2,5 10-2 kg.
Certaines ondes se propageant lors d'un séisme sont de fréquences
beaucoup plus basses ( plus petites) que celles des ondes P et S. Leur
période T=1/f est donc beaucoup plus grande que T0. La
période et la racine carrée de la masse sont proportionnelles : il faut
donc augmenter la masse m pour les enregistrer.
A
propos des séismes :
|
questions
|
réponses
|
|
A partir de l'épicentre, les ondes sismiques se
propagent-elles dans une direction privilégiée ?
|
A partir de l'épicentre, les ondes sismiques se
propagent dans toutes les directions du globe terrestre jusqu'à sa
surface.
|
|
Les ondes sismiques se propagent-elles avec
transport de matière ?
|
Les ondes transportent de l'énergie mais pas de
matière
|
|
Définir une onde longitudinale.
|
onde longitudinale : la direction de propagation a
la même direction que celle de la déformation du milieu de propagation.
|
|
Exprimer puis calculer la longueur d'onde l d'une onde P de période T=0,2 s.
|
longueur d'onde (m) = célérité (m/s) * période (s)
l = 6 103*0,2 =
1,2 103 m
|
|
Pourquoi le texte donne t-il les célérités moyennes
pour les célérités des ondes sismiques ?
|
Les ondes ne se propagent pas toutes à la même
célérité car le globe terrestre n'est pas homogène. On fait donc un
calcul de vitesse moyenne pour tenir compte de la diversité des
matéraiux du milieu de propagation.
|
|



