Aurélie 05/06
d'après concours manipulateur électroradiologie médicale AP Paris 2002

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

Faisceau d'électrons (4,5 pts)

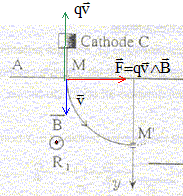
 Une cathode C est portée à haute température et émet des électrons à une vitesse négligeable devant toutes les vitesses considérées dans l'exercice. Le faisceau d'électrons émis par cette cathode est accéléré par une anode A. La différence de potentiel entre la cathode et l'anode est UAC. Le faisceau d'électrons traverse l'anode par un petit trou M et pénètre dans un région où règne un champ magnétique perpendiculaire au plan de la figure. Le faisceau d'électrons décrit un quart de cercle et pénètre dans un espace R2 sans champ magnétique où règne un champ électrique uniforme crée par l'électrode E. Le potentiel de cette électrode est inférieur à celui de l'anode A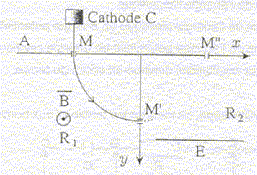

  1. Déterminer l'expression littérale de la vitesse des électrons en M. Calculer v.
  2. Déterminer le sens du champ magnétique.
  3. Montrer que l'expression du rayon de la trajectoire dans la région R1 est de la forme R= mv/(|q|B)
  4. Déterminer l'équation horaire des électrons dans la région R2. Quel doit être la valeur du champ électrique pour que les électrons passent en M" ?
    masse de l'électron m=9,1 10-31 kg ; charge de l'électron q= - 1,6 10-19 C ; UAC= 1000 V ; OM=OM'=OM"=R=10 cm
corrigé
expression littérale de la vitesse des électrons en M : le poids des électrons est négligeable ; la vitesse initiale est négligeable;

seule la force électrique effectue un travail, moteur, de valeur |q|UAM.

écrire le théorème de l'énergie cinétique entre C et M : ½mv²=|q|UAM ; v² = 2|q|/m UAM

v = ( 2|q|/m UAM)½ =(2*1,6 10-19 / 9,1 10-31 * 1000)½ =1,88 107 m/s.

sens du champ magnétique : vers l'avant

expression du rayon de la trajectoire dans la région R1 :

l'électron n'est soumis qu'à la force magnétique centripète dirigée vers le centre de l'arc de cercle.

La seconde loi de Newton s'écrit suivant l'axe n de la base de Frenet : |q|vB=mv²/ R soit R= mv/(|q|B)

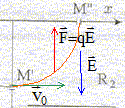
équation horaire des électrons dans la région R2 :

les électrons ne sont soumis qu'à la force électrique ; écrire la seconde loi de Newton : d'où l'accélération : ( 0 ; qE/m ) dans le repère (Ox, Oy)

la vitesse est une primitive de l'accélération : ( v0 ; qE/m t )

la position est une primitive de la vitesse : x = v0 t ; y = ½qE/m t²+R

t = x/v0 ; repport dans y : y = ½q/m E / (v0²) x² +R

en M" : x=R et y=0 d'où : ½qE / (mv0²) R² +R = 0 ; -½qE / (mv0²) R =1 ; ½|q|E / (mv0²) R =1

E= 2mv0²/ (|q|R) = 2*9,1 10-31(1,88 107 )² /( 1,6 10-19 *0,1) = 4 104 V.
Radium ( 4 pts)

Le curie est défini comme l'activité d'un gramme de radium ( 1 Ci = 3,7 1010 Bq). Le radium fut découvert en 1898. 22688Ra est émetteur a, sa période radioactive est de 1620 ans.

  1. Quelle serait en 2002, exprimée en Bq, l'activité d'un gramme de radium dont l'activité en 1898 était de 1 Ci ? Faire apparaître la résolution littérale.
  2. Pourquoi le becquerel a-t-il été préférée au curie dans le système SI.
  3. Que signifie "22688Ra est émetteur a " ?
  4. Ecrire l'équation de cette désintégration.
  5. Calculer en u la masse théorique du noyau de 22688Ra.
  6. La masse réelle du noyau de 22688Ra est 225,9771 u. Pourquoi la masse réelle est-elle différente de la masse théorique ?
  7. La masse réelle du noyau de 22286Rn est de 221,9703 u, la masse du noyau d'hélium est de 4,0015 u. Calculer en J et en MeV l'énergie libérée lors de la désintégration a d'un noyau de radium 226.
    masse : mp = 1,672 6231 10-27 kg ; mn =1,674 9286 10-27 kg ; 1 u = 1,660 5402 10-27 kg ; 1 eV= 1,602 10-19 J ; c= 3 105 km/s.
corrigé
activité actuelle d'un gramme de radium dont l'activité en 1898 était de 1 Ci :

A=A0 exp(-lt) ; l = ln2/t½ = ln2/(1620)=4,28 10-4 an-1 ; t = 2002-1898=104 ans

A=A0 exp(-ln2 t //t½)=A0 2( -t //t½) =A0 2(-104/1620) =0,956 A0 = 0,956 Ci ou 3,54 1010 Bq.

le becquerel a été préféré au curie car le curie est une unité bien trop grande.

signification de : "22688Ra est émetteur a " : lors de sa désintégration le radium 226 donne un noyau fils et un noyau d'hélium

22688Ra ---> AZX+ 42He

lois de conservation : conservation de la charge : 88 = Z+2 soit x=86 ( élément radon Rn)

conservation du nombre de nucléons : 226=A+4+y soit A=222

masse théorique du noyau de 22688Ra : 88 protons et 226-88 = 138 neutrons.

m= (88*1,672 6231 + 138*1,674 9286 )10-27 = 378,533 8636 10-27 kg

puis diviser par 1,660 5402 10-27 kg pour obtenir la masse en u : 227,958 3 u

masse réelle différente de la masse théorique :

La différence entre masse théorique et masse réelle correspond à l'énergie de liaison du noyau : un noyau est d'autant plus stable que son énergie de liaison par nucléon est grande.

énergie libérée par la réaction d'un noyau de radium 226 :

Dm= m(22286Rn) + m(42He) - (22688Ra) =221,9703 + 4,0015 - 225,9771 = -0,0053 u

puis -0,0053 *1,66 10-27 = 8,8 10-30 kg

E= |Dm|c² = 8,8 10-30 *(3108)² =7,9 10-13 J ou 7,9 10-13 /1,6 10-19 = 4,9 106 eV= 4,9 MeV
solution de soude (5,5 pts)

On prépare une solution de soude en dissolvant 10 g de pastilles d'hydroxyde de sodium dans 5 L d'eau distillée.

  1. Ecrire l'équation bilan de la dissolution.
  2. Après en avoir donné la formule, calculer la concentration massique en soude de la solution.
  3. Après avoir donné la formule de la concentration molaire, montere le rapport qui existe entre la concentration massique c et la concentration molaire C.
  4. Calculer la concentration molaire de la solution.
    Na : 23 ; O : 16 ; H : 1 g/mol.

Soit une solution de soude (S1) de concentration molaire égale à 0,01 mol/L. On souhaite neutraliser 250 mL de la solution S1 par 750 mL d'une solution acide S2.

  1. Quel volume de chlorure d'hydrogène faut-il dissoudre dans 750 mL d'eau pour que la neutralisation ait lieu ?
  2. Quel était le pH de la solution S2 ?
  3. Ecrire l'équation bilan de la réaction de neutralisation.
  4. Quel volume d'eau de la solution finale faut-il évaporer pour que la concentration massique soit de 9 g/L ?
    Vm= 24 L/mol ; Cl : 35,5 g/mol

 

corrigé
équation bilan de la dissolution : NaOH (s) = Na+(aq) + HO-(aq)

concentration massique en soude ( g/L)= masse (g) / volume de la solution (L) = 10/5 = 2 g/L

concentration molaire de la soude : C(g/mol) = quantité de matière (mol) / volume de la solution (L)= n/V

Quantité de matière (mol) = masse (g) / masse molaire (g/mol)= m/M

d'où : C = m/(MV) = c/M soit C= 2/(23+16+1) = 0,05 mol/L.

volume de chlorure d'hydrogène :

à l'équivalence du titrage, les quantité de matière des réactifs sont en proportions stoechiométriques.

n( acide ) = V/Vm = V/24 =4,167 10-2 V mol avec V : volume de chlorure d'hydrogène.

n(soude) = 0,25*0,01 = 2,5 10-3 mol

2,5 10-3 =4,137 10-2 V ; V = 2,5 10-3 /4,167 10-2 = 0,06 L.

pH de la solution S2 : n(HCl = n(H3O+) = 0,06/24 = 2,5 10-3 mol dans 0,75 L

d'où [H3O+]= 2,5 10-3 /0.75 =3,33 10-3 mol/L ; pH= -log [H3O+] = - log 3,33 10-3=2,47

équation bilan de la réaction de neutralisation :

H3O+ + Cl- + Na+ + HO- = 2H2O + Cl- + Na+.

volume d'eau de la solution finale à évaporer :

le volume initial du mélange est 1L ; la solution de chlorure de sodium obtenue après neutralisation compte : 2,5 10-3 mol de NaCl dans 1 L.

Après évaporation la concentration molaire en chlorure de sodium est : 9/(23+35,5 ) = 0,154 mol/L

d'où 0,154 V= 2,5 10-3 avec V : volume final après évaporation soit V= 2,5 10-3 / 0,154 = 1,625 10-2 L

On a donc évaporé : 1-1,625 10-2 = 983,7 mL.
(2,5 pts)

 

  1. Quelle différence structurelle existe-t-il entre 126C et 146C ?
  2. Que sont ces deux nucléides l'un pour l'autre ?
  3. Une molécule peut-elle être formée indifféremment avec l'un ou l'autre de ces deux nucléides ? Les molécules ainsi formées ont-elles même propriétés chimiques ? Justifier.
  4. Dans la classification périodique des éléments, la masse atomique de l'élément chlore est de 35,5 g/mol. Quel est le sens de cette phrase ? Pourquoi la masse molaire est-elle exprimée avec un nombre décimal ?

     

corrigé
126C et 146C ne différent que par leur nombre de neutrons ( respectivement 6 et 8) : ce sont deux isotopes.

Une molécule peut être formée indifféremment avec l'un ou l'autre de ces deux nucléides. Les propriètés chimiques sont identiques ( celles-ci dépendent essentiellement du nombre d'électrons externes et non pas du nombre de neutrons) ; les propriètés physiques qui dépendent de la masse sont légèrement différentes.

La masse d'une mole d'atomes de chlore ( soit 6,02 1023 atomes) est 35,5 g.

Masse molaire = S % de chaque isotope * masse molaire de cet isotope / 100

Dans le cas du chlore : 37Cl : 25% et 35Cl : 75 % : d'où une masse molaire exprimée avec un nombre décimal.
retour -menu