Aurélie 03/04/06

Rotation d'un miroir

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


. .


.
.


rotation d'un miroir ( 12 pts)

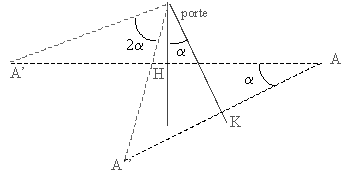
Une porte de 80 cm de large est recouverte d'un miroir. Un observateur situé à 1,00 m en face de cette porte fermée observe son image. Une autre personne ouvre la porte : le centre de la porte s'éloigne alors de l'observateur immobile qui perd rapidement de vue son image. En assimilant l'observateur à un point A situé sur la normale au plan de la porte fermée passant par son centre :

  1. Schématiser la situation après ouverture de la porte.
  2. Déterminer l'angle a de rotation de la porte à partir duquel l'observateur ne se voit plus dans le miroir. Faire un schéma illustrant la situation.
  3. Si a = 45°, quel déplacement minimal doit suivre A pour se voir de nouveau dans le miroir. Un schéma clair est exigé.
corrigé
A' image de A quand la porte est fermée ( A et A' sont symétriques par rapport au plan de la porte)

A'" image de A quand la porte est fermée ( A et A'' sont symétriques par rapport au plan de la porte)

Dés que l'image A" sort du champ visuel de l'observateur, ce dernier ne se voit plus dans le miroir.

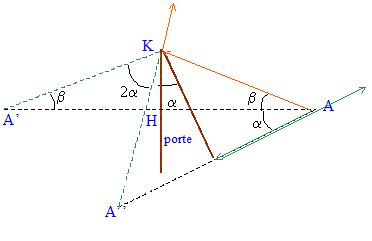
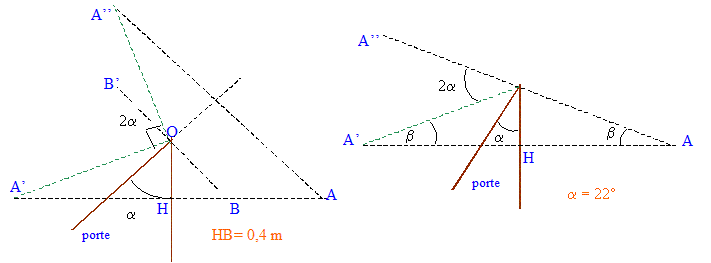
tan b = 0,4/1 = 0,4 soit b =21,8 ° ; AK = (1² + 0,4²)½=1,077 m

sin ( a+b) = 0,8 / 1,077 = 0,743 soit a+b = 48 ° ; d'où a = 48-21,8 = 26,2°.

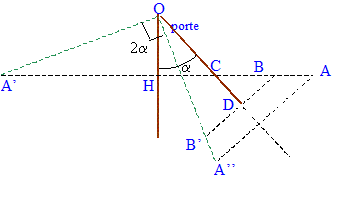
L'observateur doit venir en B afin de voir son image B'.

Dans les triangles OHC et DBC : OC = 0,4*2½ =0,566 m ; CD= DB = 0,8-0,566 = 0,234 m

CB = 0,234*2½ = 0,33 m soit HB= 0,4+0,33 = 0,73 m

ouverture en sens contraire :

retour -menu