|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
||||
| .
. |
||||
|
||||
|
|
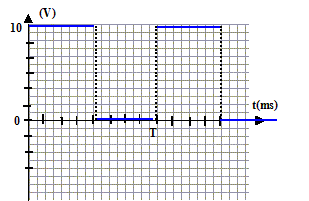
On associe en série un générateur basse fréquence (GBF), un résistor (R= 10 kW) , un condensateur de capacité C= 10mF et un interrupteur. Le GBF délivre une tension u, rectangulaire telle que : u(t)=U0 =10 V sur l'intervalle [0 ; ½T] et u(t) = 0 sur l'intervalle [½T, T]
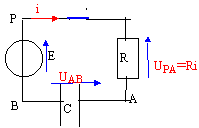
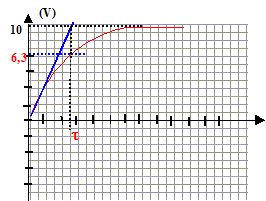
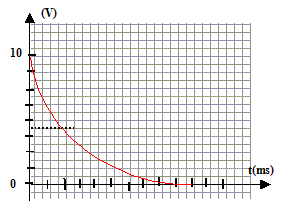
u(t) sur l'intervalle [0, 2T] uPB= U0 ; uPB= uPA+ uAB avec i = dqA/dt = CduAB/dt . U0 = Ri +uAB soit U0 =RC duC/dt +uC (1) uc= A(1-exp(-at)) dériver l'expression de uC par rapport au temps : duC/dt = Aa exp(-at). repport dans (1) : U0 = RCAa exp(-at)+A(1-exp(-at)) U0 = A(RCa -1)exp(-at) +A égalité vérifiée quel que soit le temps, en conséquence A= U0 et a =1/(RC) = 1/(104*10-5) = 10 s A : amplitude de la tenion uC (V) ; a =1/(RC) inverse de la constante de temps ( seconde-1 ) du dipôle RC. uC(t) = U0(1-exp(-t/(RC)))= 10 ( 1-exp(-10t)) la solution trouvée satisfait aux conditions initiales en effet : uC(0) = 10(1-exp(0)) = 0 ( condensateur non chagé) allure de la courbe uc(t)
dans le cas ou ½T est très supérieur au produit RC. énergie stockée à chaque instant par le condensateur :
½CuC². ln(10-3) = -10 t1
; t1 = -0,1 ln(10-3) =0,69 s.
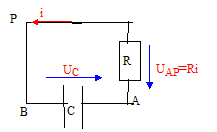
uC(t') = Ri avec i = -dq/dt et q= CuC soit i = -CduC/dt uC(t')+RCduC/dt =0 (1) solution de l'équation différentielle : uc= Bexp(-bt). Valeurs de B et b : dériver l'expression de uC par rapport au temps : duC/dt = -Bb exp(-bt). repport dans (1) : B exp(-bt)
-Bb RC exp(-bt) =0 égalité vérifiée quel que
soit le temps, en conséquence b =1/(RC)
= 1/(104*10-5) = 10 s à l'instant t'=0 uc(0) = U0
= 10 V d'où B = 10 V et uc= 10 exp(-10t). La solution trouvée
satisfait aux conditions initiales énergie stockée à chaque instant par le condensateur :
½CuC². uC(t'2) = 0,37 *10 = 10 exp(-10t'2) ; 0,37 = exp(-10t'2) ; -10t'2 = ln 0,37 = -1 soit t'2 = 0,1 s.
|
|||
|
|