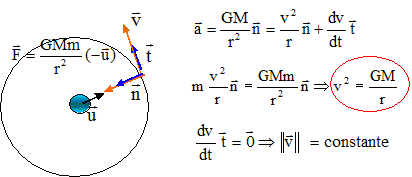|
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
On étudie le mouvement d'un satellite de masse m d'une planète de masse M dans le référentiel géocentrique de celle-ci ( M est très grand devant m). Les deux objets présentent des répartition de masses à symétrie sphérique, autour d'un point G pour le satellite et du point O pour la planète. Les vecteurs sont écrits en bleu et en gras.
corrigé Expression de la force de gravitation exercée par la planète sur le satellite : Relation qui lie la vitesse v de G, la masse M de la planète, le rayon r de l'orbite et G : On utilisera les notations suivantes : u=OG/OG et r=OG.
On suppose dans la suite que le mouvement de G est circulaire uniforme de centre O. Expression de v en fonction de la période T du mouvement et du rayon r : 3ème loi de Kepler r3/T2 = constante La période de révolution T du satellite (seconde) est le temps mis par le satellite pour faire un tour et ce d'un mouvement uniforme. 2 p r =vT élever au carré, puis remplacer v² par l'expression ci dessus. 4p² r ² = v² T² = GM/ r T² ou T² =4p² /(GM)r3. soit T² /r3 = 4p² / (GM) rapport constant pour une planète donnée.(3ème loi de Kepler) distance en mètre, période en seconde, masse en kg. Estimation de la masse d'Uranus : Les valeurs de T et r
pour 5 satellites d'Uranus sont données :
M= 4*3,14²/(6,67 10-11 *6,74 10-15 ) = 8,77 1025 kg.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
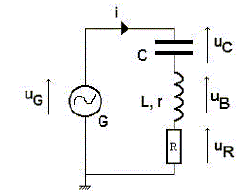
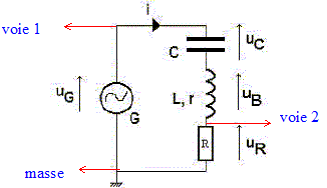
G : générateur basse fréquence délivrant une tension sinusoïdale de valeur efficace U= 60 V fixe et de fréquence f réglable. C ; condensateur de capacité C inconnue. Bobine d'inductance L= 60 mH et de résisatnce r = 4 W. Conducteur ohmique de résistance R= 1,5 kW.
corrigé Relation entre uG, uB, uR et uC : additivité des tensions uG = uB + uR + uC Expression de duC/dt en fonction de C et i : q= CuC ; i = dq/dt = CduC/dt uR= Ri = RC duC/dt
; uB = Ldi/dt + r i = LCd²uC/dt²
+ r CduC/dt uG = uC +
(R+r)CduC/dt + LCd²uC/dt²
Ce type de phénomène peut se produire dans certains systèmes mécaniques : amortisseur d'une voiture ( résonateur ) ; une route
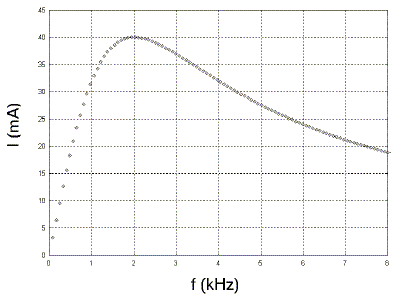
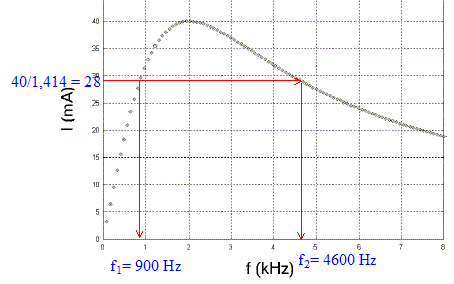
pleine de trous joue le rôle d'excitateur. Expression théorique de cette valeur notée Ithmax en fonction de U, R et r : Ithmax = U/(R+r) = 60 / 1504 = 3,99 10-2 A, en accord avec la valeur lue sur le graphe. Fréquence fmax correspondant au maximum d'intensité : 2000 Hz Valeur de la capacité C du condensateur : à la résonance LCw0²=1 avec w0 = 2pfmax =1,256 104 rad/s. C= 1/(Lw0²)
= 1/(0,06*(1,256 104)2) =
1,1 10-7
F.
Branchements à effectuer pour visualiser uG sur la voie 1 et uR sur la voie 2 d'un oscilloscope :
P= 1504*(28,2 10-3)2
= 1,2 W. P= 1504*(17 10-3)2 = 0,44 W.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|