|
Données : 10½
= 3,2 ;
3½
=1,7 ; 5½ =2,2 ; 2½ =1,4
; g = 10 m/s².
à
propos d'équation différentielle.
-
On considère un poids lours descendant sans
freins, le long d'une pente, et sur lequel s'exercent des frottements
dépendant uniquement de son poids. Parmi les équations différentielles
ci-dessous, laquelle permet de décrire l'évolution du système :
|
A
|
B
|
C
|
D
|
|
aX"+b=0
|
aX"+bX+c=0
|
aX'+bX=0
|
aX'+bX+c=0
|
Le camion est soumis à son poids, vertical vers le bas, valeur Mg, à
l'action du plan perpendiculaire au plan, au frottements colinéaires à
la vitesse et de sens contraire, valeur kMg ( k = constante).
Ecrire la seconde loi de Newton sur un axe parallèle à la pente,
orienté vers le bas : Mg sin a
-kMg = MX" du type aX"+b=0.
-
On considère un condensateur en train de se
charger. Parmi les équations différentielles ci-dessous, laquelle
permet de décrire l'évolution du système :
|
A
|
B
|
C
|
D
|
|
aX"+b=0
|
aX"+bX+c=0
|
aX'+bX=0
|
aX'+bX+c=0
|
Condensateur, résistor en série avec un générateur de tension continue
de fem E. Les tensions aux bornes des dipôles s'ajoutent : uC
+ Ri = E
avec q=CuC soit uC=
q/C et i = dq/dt = q' d'où q/C + Rq'= E soit Rq' + q/C-E=0 du type aX'+bX+c =0.
On
considère une bouée qui remonte des profondeurs d'un lac. Parmi les
équations différentielles ci-dessous, laquelle permet de décrire
l'évolution du système
|
A
|
B
|
C
|
D
|
|
aX"+b=0
|
aX"+bX+c=0
|
aX'+bX=0
|
aX'+bX+c=0
|
La bouée ( volume V) est soumise à son poids, verticale, vers le bas,
valeur Mg, à la poussée d'Archimède, verticale, vers le haut, valeur
constante reaugV,
à une force de frottement fluide, colinéaire à la vitesse, de sens
contraire, valeur kv ( aux faibles vitesses)
Ecrire la seconde loi de Newton sur un axe
vertical, orienté vers le haut : Mg - reaugV
-kv = MX" soit MX"+kX'+reaugV-Mg=0
du type aX"+bX' +c=0.
à propos d'horloge
- Soit une horloge à pendule, fonctionnant
parfaitement, de période T=1,0 s. L'horloge est dans un ascenseur au
niveau du sol et indique la date : 12 h 00 min 00 s. A cet instant
précis, l'ascenseur un peu fou démarre avec une accélération constante
de 10 m/s². Quand l'ascenseur passe à la côte 100 m, la date indiquée
par l'horloge est : 12 h 00 min 8,9 s ; 12 h 00 min 13,3 s ; 12 h 00
min 6,3 s ; 12 h 00 min 10,8 s ;
Référentiel terrestre ; axe vertical orienté vers le haut : période du
pendule simple : T = 2p
(L/g)½ au sol.
dans le référentiel de l'ascenseur l'accélération est : g + a=2g ; la
période devient T' = 2p
(L/(g+ a))½
T'=2p (L/(2g))½
=2-½2p
(L/(g))½ = 2-½ = 0,7 s.
Durée de la montée mesurée par une horloge au sol
: h=½at² soit t²= 2h/a = 200 /10 = 20 ; t = 1,4*3,2 =4,48 s.
Durée indiquée par l'horloge : 4,48/0,7 = 6,3 s.(12 h 00 min 6,3 s)
- L'ascenseur précédent coupe son accélération juste au
moment où il passe à la côte 100 m. Ensuite il poursuit son ascension
jusqu'à la côte 300 m à vitesse constante. A l'instant où il passe à la
côte h = 300 m, il se met à décélérer de telle sorte que quand il
arrive à la côte 400 m il est à l'arrêt. A cet instant précis la date
indiquée par l'horloge est : 12 h 00 min 8,9 s ; 12 h 00 min 13,3 s ;
12 h 00 min 6,3 s ; 12 h 00 min 10,8 s .
200 m sont parcourus d'un mouvement uniforme durant lequel T= 1s.
Vitesse de l'ascenseur à t = 4,48 s. v = at = 10*4,48 = 44,8 m/s
Durée de cette phase : 200/44,8 = 4,46 s
Lors de la décélération l'horloge embarquée est à l'arrêt (dans le
référentiel de l'ascenseur l'accélération est : g - a =0)
Durée indiquée par l'horloge : 4,46 + 6,3 = 10,76 s (12 h 00 min 10,8 s)
-
- Dans l'ascenseur précédent on remplace l'horloge à
pendule par une horloge à ressort : système oscillant que nous
schématisons par un ressort horizontal de raideur k et une masse m qui
lui est accrochée. Quand l'ascenseur passe à la côte 100 m, la date
indiquée par l'horloge est : 12 h 00 min 8,9 s ; 12 h 00 min 13,3 s ;
12 h 00 min 6,3 s ; 12 h 00 min 10,8 s
La période de l'oscillateur élastique est indépendante de
l'accélération.
- La date indiquée par l'horloge à l'arrivée à la côte
400 m est : 12 h 00 min 8,9 s ; 12 h 00 min 13,3 s ; 12 h 00 min 6,3 s
; 12 h 00 min 10,8 s
à propos d'un circuit électrique
On considère un générateur de tension continue de
fem 12 ,0 V et de résistance interne 4,0 W.
- Si on branche ce générateur à un circuit extérieur
consommant une puissance de 6,0 W, l'intensité du courant dans le
circuit vaut : 0,65 A ; 1,0 A ; 2,35 A ; 2,7 A ; 3,5 A.
Puissance délivrée par le générateur au circuit P= UI =6,0 W avec U =
E-rI, tension aux bornes du générateur.
(E-rI)I= P soit (12-4I)I=6 ; -4I²+12I-6=0 ; I²-3I+1,5 = 0 ; résoudre :
I= 0,65 A et I= 2,35 A.
- La puissance maximale disponible aux bornes de ce
générateur est : 9,0 W ; 8,0 W ; 7,0 W ; 6,0 W ; 5,0 W.
P= (12-4I)I = 12I-4I² ; dériver P'= 12-8I ; la dérivée s'annule pour I=
1,5 A d'où Pmax = 9 W.
L'intensité maximale du courant que peut impulser ce générateur est
alors : 3,5 A ; 2,5 A ; 1,5 A
; 0,5 A ; 1,0 A
- Dans les conditions des deux questions précédentes,
le rendement du générateur est en % : 10 ; 20 ; 30 ; 50 ; 70.
Tension aux bornes du générateur : U= P/I= 9/1,5 = 4,5 V ; rendement
U/E*100 = 50 %.
à propos d'optique
- On veut obtenir à travers une lentille convergente de
vergence C, une image droite et trois fois plus grande que l'objet
observé. La position de l'objet par rapport à la lentille est = -3f ;
-2 f ; -2/3 f ; 2/3 f ; 2 f. ( avec f : distance focale de la lentille)
La lentille doit fonctionner en loupe pour avoir une image droite, plus
grande que l'objet. Donc la distance lentille objet est inférieure à f.
L'objet est à gauche de la lentille, l'axe optique est orienté vers la
droite : position de l'objet : -2/3 f.
- Dans le cadre de
l'optique géomètrique une lentille parfaite donne d'un point objet, un
point image. On considère la pupille d'un oeil normale
comme une lentille parfaite. Sachant que la rétine est à 2,0 cm en
arrière de la pupille et que les cellules photosensibles qui la
tapissent sont séparées par une distance minimale de 1,5 mm, la limite de résolution
angulaire de cet oeil est : 60 mrad
; 65 mrad ; 70 mrad ; 75 mrad
; 80 mrad ;
1,5 / 0,02 = 75 mrad
A propos d'un graphique
Le graphique
ci-dessous peut correspondre à quel(s) phénomène(s) physique(s) parmi
les suivants :

A- La tension aux
bornes d'une bobine pendant sa mise sous tension à travers une
résistance.(faux)
B- L'intensité du courant qui traverse la bobine pendant sa mise sous
tension ( vrai)
C- L'intensité du courant qui traverse la bobine pendant la coupure du
courant ( faux, la fonction ci-dessus est croissante)
D- La charge d'un condensateur à travers une résistance ( vrai )
E- L'intensité du courant qui parcourt le circuit précédent pendant la
charge du condensateur ( faux)
A propos de mécanique
- Un observateur est
dans une station spatiale placée sur une orbite géostationnaire.
( La station spatiale paraît immobile pour un observateur terrestre )
A- Il voit la Terre tourner autour de lui avec une période de 24 H (
faux)
B- Il voit le Soleil tourner autour de lui avec une période de 24 H (
faux : la Terre donc la station tourne autour du soleil )
C- Il tourne autour du Soleil en 365 jours ( vrai)
D- Il voit la Terre dans la même direction à tout instant (vrai)
E- Notre observateur est de type galiléen. (faux)
- Dans un mini-golf, un joueur doit frapper une balle
en A de telle sorte que cette balle parcourt la distance AB horizontale
; ensuite elle aborde en B un demi-cercle vertical et le quitte en C,
pour finalement tomber dans le trou G
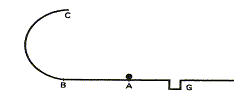
Si le demi-cercle a un rayon de 50 cm et le trou est
à 2,0 m de B, la vitesse ( en m/s) à imprimer à la balle au moment de
la frappe pour réussir le"trou" est : 4,4 ; 5,4 ; 5,8 ; 6,4 ; 6,7. La
balle est considérée comme ponctuelle et se déplace sans frottement.
Entre C et G , chute libre avec vitesse initiale horizontale , valeur vC.
y= - ½gx²/v²C+BC ; au sol y=0 soit v²C
=10*2²/2 = 20 ;
Entre B et C seul le poids travaille ; le th. de l'énergie cinétique
s'écrit : v²C -v²A =
-2gBC ; v²A =v²C +2gBC=40
; vA= 6,3 m/s.
A propos de magnétisme
- Un conducteur rectiligne de longueur L= 10 cm et
parcouru par un courant d'intensité 4,0 A est
placé dans un champ magnétique de valeur B= 0,040 T. Si l'angle entre
le conducteur et la direction du champ fait 30°, alors la force de
Laplace exercée sur le conducteur, exprimée en N vaut : 2,0 10-3
; 8,0 10-3 ; 1,4 10-2 ;
2,8 10-2 .
F = BIL sin 30 = 0,04*4*0,1*0,5 = 8,0 10-3 N
A propos d'onde
- Une onde monochromatique appartenant au spectre
visible :
A- est diffractée lorsqu'elle change de milieu de propagation ( faux,
il s'agit de réfraction)
B- est dispersée si sa célérité dépend de la nature du milieu de
propagation.( faux, si la célérité dépend de la fréquence)
C- possède une période de l'ordre de 1015 s.
(faux)
D- possède une fréquence plus grande que celle d'une onde infra-rouge (
exact )
E- a dans un milieu d'indice n une longueur d'onde n fois plus grande
que dans le vide.( faux l
= l 0/n)
A propos d'énergie nucléaire
- A- la fission d'un noyau lourd nécessite une
température très élevée. (faux, c'est la fusion)
B- plus l'énergie de liaison d'un noyau est élevée, plus le noyau est
stable.(faux )
C- plus la constante de désintégration d'un noyau radioactif est
grande, plus le noyau est instable
D- plus l'énergie moyenne de liaison par nucléon d'un noyau est grande,
plus ce noyau est stable (vrai)
E- La masse d'un noyau est égale à la somme des masses des nucléons qui
le composent . ( faux)
- On injecte dans le sang d'un patient 10 mL d'une
solution contenant du 24 Na à une
concentration de 1,0 10-3 mol/L. Au bout de 15
heures on prélève à notre patient 10 mL de sang. On trouve alors une
concentration de 24 Na égale à : 1,0 10-6
mol/L. Le sodium est uniformément répati dans tout le volume sanguin.
Le volume sanguin ( en L) du patient est de : 4,5 ; 5 ; 5,5 ; 6 ; 6,5.
La demi-vie du sodium 14 est de 15 heures.
Quantité de matière initiale de sodium 24 : 10-3*0,01
= 10-5 mol
Quantité de matière de sodium 24 à t½ : ½ 10-5
= 5 10-6 mol ; concentration : 5 10-6
/ V avec V (en L) volume du sang
|