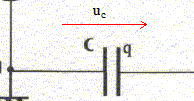|
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
A- Réglage du spectrophotomètre : on
doit régler la longueur d'onde de la lumière pour laquelle l'absorption
de la solution est maximale. La seule espèce chimique colorée est l'ion
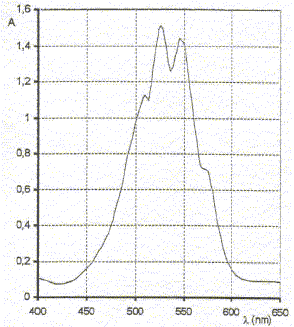
permenganate. On réalise le spectre d'une solution diluée de
permanganate de potassium, pour choisir cette longueur d'onde.
B- Etalonnage du spectrophotomètre : on mesure l'absorbance de solutions de concentrations connues de permanganate de potassium pour la longueur d'onde lf .
C- Suivi spectrophotométrique : dans un bécher de 50 mL, on mélange V1= 10,0 mL d'une solution de permanganate de potassium acidifié de concentration C1 = 1,0 10-3 mol/L. On ajoute une pointe de spatule de nitrate de manganèse Mn(NO3)2 : les ion Mn2+ jouent le rôle de catalyseur. A la date t=0 on ajoute V2 = 10 mL d'une solution d'acide oxalique de concentration C2 = 1,0 10-2 mol/L. On homogénéise et on verse une partie du mélange dans la cuve du spectrophotomètre. Toutes les minutes on note la valeur de l'absorbance de la solution.
corrigé domaine et quelle gamme de longueur d'onde : dans l'intervalle [500 ; 560 nm] ( vert) l'absorption de la solution est très grande. longueur d'onde lf pour faire les mesures d'absorbance de la solution de permanganate de potassium : 530 ou 550 nm La couleur des solutions de permanganate de potassium
est en accord avec le spectre d'absorption proposé : la solution
absorbe le vert ; la couleur complémentaire du vert est le rose violet,
couleur de l'ion permanganate.
Préparer à partir de la solution C0 un volume de 100 mL de la solution C2. facteur de dilution F= C0 /C2 = 0,5/0,1 = 5 ; volume fiole jaugée ( 100 mL) / volume pipette jaugée = 5 Prélever 20 mL de solution mère C0 à l'aide d'une pipette jaugée + pipeteur. Placer dans une fiole jaugée de 100 mL et compléter avec de l'eau distillée jusqu'au trait de jauge. agiter pour rendre homogène.
5 fois { C2H2O4 = 2 CO2 + 2H+ + 2e- }oxydation puis additionner : 2 MnO4- + 5 C2H2O4 + 16H+ + 10e- = 2 Mn2+ + 8 H2O+ 10 CO2 + 10H+ + 10e- 2 MnO4- + 5 C2H2O4 + 6H+ = 2 Mn2+ + 8 H2O+ 10 CO2 Quantité de matière initiale en acide oxalique (mol) = concentration (mol/L) * volume (L) n C2H2O4= V2C2 = 10 * 10-2 = 10-1 mmol n( MnO4- ) = V1C1 = 10 * 10-3 = 10-2 mmol
Les quantités de matière sont en proportions stoéchiomètriques si : nMnO4- = 2/5 n C2H2O4 = 0,4*0,1 = 0,04 mmol Or on ne dispose que de 0,01 mmol MnO4- : ce dernier est en défaut ; l'acide oxalique est en excès.
vitesse volumique v de la réaction en fonction de
l'avancement x : v = 1/VT
dx/dt avec VT (L) volume total du mélange et x
avancement (mol)
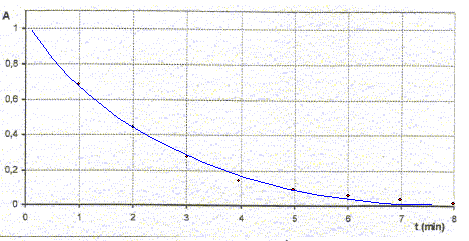
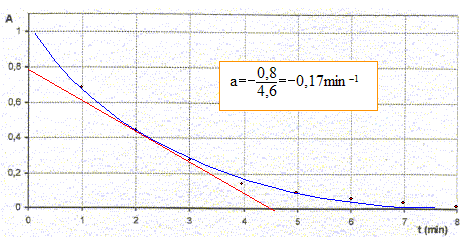
relation entre x et l'absorbance At : At = k [MnO4-]t ; n10 -x =AtVT /k ; [MnO4-] 0 VT -x = AtVT /k ; At= ½C0 k -kx/ VT. expression de la vitesse volumique v en fonction de At, k et x : dAt/dt = -k/VT dx/dt ; dAt/dt = -k v ; v = -1/k dAt/dt Déterminer le coefficient directeur de la tangente à la courbe A=f(t) à la date t= 2 min puis diviser par -k = -2 103 L/mol.
v = 0,17/2 103 = 8,4 10-5 mol L-1 min-1. La vitesse diminue au cours du temps car les coefficients directeurs des tagentes diminuent ( les tangentes se rapprochent de l'horizontale) Calcul de A0 : A0= ½ C0 k = ½ 10-3 * 2 103 = 1. temps de demi réaction t½ : durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final. xt½= ½xfin = 5 10-6 mol ; At½ = ½C0 k -kxt½/ VT = 1-2 103*5 10-6 / 0,02 = 0,5 lecture graphe : t½ voisin 1,7 min.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
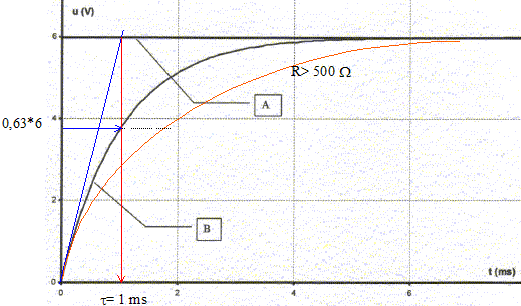
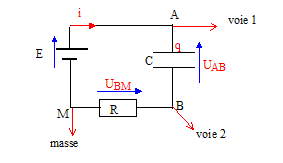
R= 500 W. Un oscilloscope à mémoire suit l'évolution temporelle des deux tensions. A la fermeture de l'interrupteur (t=0) le condensateur est initialement déchargé. 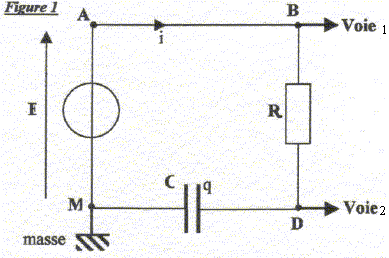
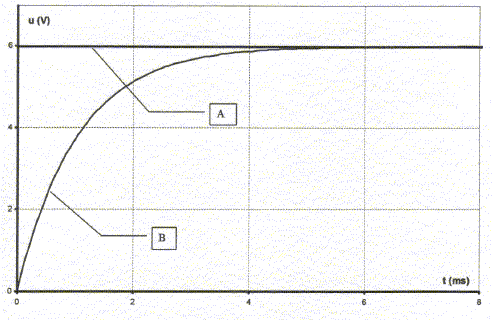
corrigé tensions mesurées sur chaque voie : voie 1: uBM tension aux bornes du dipole RC ou bien tension E aux bornes du générateur de tension ; voie 2 : tension uDM aux bornes du condensateur. la courbe A montre une tension constante uBM =E=6 V La courbe B visualise une tension croissante (
exponentielle) au cours du temps : tension uDM
aux bornes du condensateur durée pour charger complétement le condensateur : en fin de charge tension uDM aux bornes du condensateur = E = 6 V d'où la durée : 5,2 ms ( lecture graphe) pour charger moins vite le condensateur, augmenter la constante de temps t= RC, donc prendre une plus grande valeur de R.
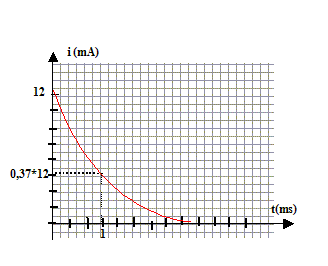
équation différentielle relative à uc: additivité des tensions : E=uAM = uAD+uDM = Ri + uc. i = dq/dt et q=Cuc d'où i= Cduc/dt. E= RCduc/dt +uc. duc/dt +uc/t =E/t avec t =RC uc = E[1-exp(-t/t)] ; duc/dt =E/t exp(-t/t) repport dans l'équation différentielle E/t exp(-t/t) +E/t[1-exp(-t/t)] =E/(RC) vérifiée pout tout t si t=RC si t=t : uc/E= 1-exp(-1)= 1-0,37 = 0,63 ; si t=5t : uc/E= 1-exp(-5)=1-0,0067 = 0,993 à t= 5t on peut considérer que la charge du condensateur est égale à 99 % de la charge complète. expression de i(t) : i(t) = Cduc/dt =E/R exp(-t/t) = I0exp(-t/t) avec I0 = E/R = 6/500 = 12 mA
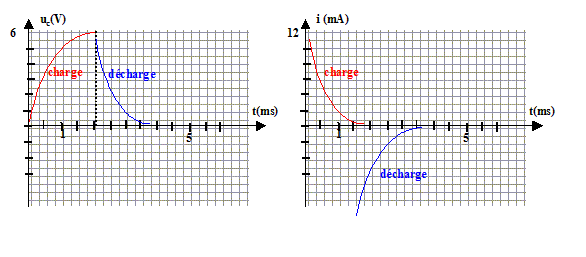
L'allure de cette courbe i(t) pourait être fournie par la tension aux bornes du résistor au facteur R près : la tension aux bornes d'un résistor et l'intensité qui le traverse sont proportionnelles.
L'intensité est une fonction discontinue. La tension uc est une fonction continue.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

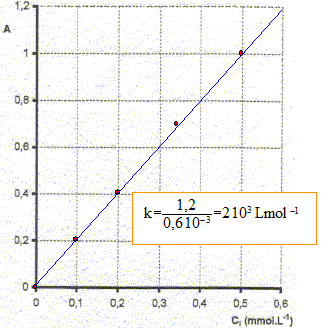 fonction linéaire A= k Ci
.
fonction linéaire A= k Ci
.