I. Une masse m est lancée de A avec la vitesse Vo = 3 m/s vers le bas du plan incliné.

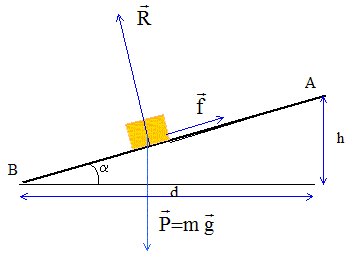
g = 10 m/s² ; f= 0,7 N ; m= 100 g ; h= 3 m ; d=4 m ; AB= 5 m.
1. m s'arrête-t-elle au bout de 3 s ?

La vitesse est une de l'accélération : v = - t + V0 = -t+3
arrêt si v=0 soit à t=3s.

2. m atteint-elle B ?
la distance est une de la vitesse : d= -½t² +3t
en B : d = 5 m
résoudre l'équation : -½t² +3t = 5
Le discriminant étant négatif, il n'y a pas de solution : la masse ne peut atteindre B; elle s'arrête avant.

3. m s'arrête-t-elle 50 cm avant B ?
La masse m s'arrête près 3 s
distance parcourue : d= -0,5 *3²+3*3 = 4,5 m

4. m passe-t-il au milieu de AB une seconde après son départ ?
distance parcourue en 1 s : d= -0,5*1²+3 = 2,5 m.

5. Quand m passe au milieu de AB, sa vitesse vaut-elle 1,5 m/s ?
vitesse à t= 1 s : v= -1+3 = 2 m/s.

II.
Une masse m= 100g glisse de A en B sur un plan incliné d'un angle "alpha" sur l'horizontale. sin "alpha" = 0,2. g= 10 m/s².
x est la position du centre d'inertie de la masse.

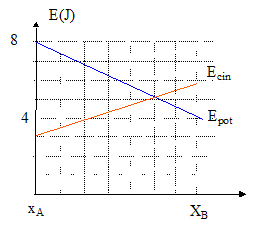
1. Le mouvement de m est-il rectiligne uniforme ?
La trajectoire est une droite : le mouvement est rectiligne.
d'après le graphe, l'énergie cinétique est une fonction croissante de l'abscisse x : l'énergie cinétique n'est pas constante et donc la valeur de la vitesse n'est pas constante : le mouvement n'est pas uniforme.

2. m est-elle soumise à des frottements ?
Energie mécanique = énergie potentielle + énergie cinétique
En A : Em= 8+3 = 11 J ; en B : 6+4 = 10 J.
L'énergie mécanique n'est pas : donc il existe des frottements.

3. La différence d'altitude entre A et B vaut-elle 2 m ?
Origine des altitudes choisie au sol.
Energie potentielle de pesanteur : Epot = mgh = 0,1*10 h = h
En A : altitude = 8 m; en B : altitude= 4 m.

4. Le rapport des vitesses de m en A et en B vaut 'il : Va/Vb = 0,5 ?
Energie cinétique en A : ½mV²a= 3
Energie cinétique en B : ½mV²b = 6
V²a/V²b = ½
(Va/Vb)²=0,5.

III
Une masse m ponctuelle est attachée à un fil sans masse, inextensible, de longueur AM= L m est lachée sans vitesse initiale d'un angle "téta 0". m est en contact avec le plan incliné et on néglige les frottements. On se place dans le cas des petites oscillations si bien que sin "téta" voisin de "téta" radian.


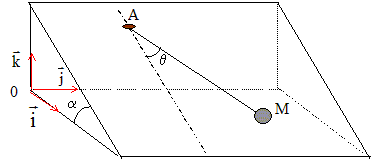
1. La réaction du plan est-elle dirigée suivant k ?
La réaction du plan sur m est au plan.



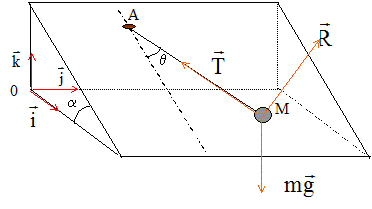
2. La période du pendule est-elle indépendante de "téta"
Vrai pour les petites oscillations.

3. Le carré de la pulsation du mouvement vaut-il : g/ L sin "alpha" ?
Dans le cas d'un pendule oscillant dans le plan , le carré de la pulsation vaut : g/L
Dans notre cas, il suffit de remplacer g par :g sin "alpha".

4. La fréquence du mouvement vaut-elle 2pi racine carrée (L/g) ?
pulsation (/s)= 2 pi fois la fréquence (Hz)

5. La norme de la réaction R du plan avec m vaut-elle mg cos"alpha" ?
exact


au plan.



2. La période du pendule est-elle indépendante de "téta"
Vrai pour les petites oscillations.

3. Le carré de la pulsation du mouvement vaut-il : g/ L sin "alpha" ?
Dans le cas d'un pendule oscillant dans le plan , le carré de la pulsation vaut : g/L
Dans notre cas, il suffit de remplacer g par :g sin "alpha".

4. La fréquence du mouvement vaut-elle 2pi racine carrée (L/g) ?
pulsation (/s)= 2 pi fois la fréquence (Hz)

5. La norme de la réaction R du plan avec m vaut-elle mg cos"alpha" ?
exact