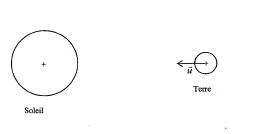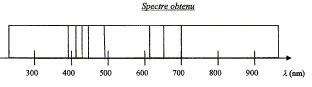Aurélie 14/06/07
 

Les étoiles filantes ; gravitation, spectre d'émission bac S 2007 Afrique

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.

Des comètes circulent dans le système solaire et laissent dans leur sillage des grains de matière de tailles plus ou moins importantes. Il arrive que la Terre croise ces grains de matière abandonnés par une comète derrière elle et qui pénètrent alors dans l'atmosphère terrestre. Lors de leur chute, ils échauffent les gaz de l'atmosphère qui émettent de la lumière pour éliminer l'énergie reçue lors de cet échauffement. On peut alors observer des phénomènes bien connus : les étoiles filantes.

Masse de la Terre : Mt= 5,98.1024 kg ; masse du Soleil: Ms = 1,98.1030 kg ; constante de gravitation universelle : G = 6,67.10-11 SI ; célérité de la lumière dans le vide : c = 3,00.108m/s ; constante de Planck : h = 6,62.10-34 J.s ; 1 eV (électronvolt) = 1,60.10-19 J

Mouvement de la Terre

On considère le mouvement de la Terre autour du Soleil dans le référentiel héliocentrique considéré comme galiléen. On suppose que ce mouvement est circulaire uniforme, de rayon R = 1,50 1011 m. On néglige l'action de tout autre astre. On s'aidera du schéma suivant :

 

  1. Donner l'expression vectorielle de la force subie par la Terre en utilisant le vecteur u du schéma.
  2. Énoncer, puis appliquer la deuxième loi de Newton à la Terre.
  3. En déduire l'expression du vecteur accélération de la terre ; on donnera sa direction, son sens et l'expression de sa norme ; le représenter sans considération d'échelle sur le schéma.
  4. On rappelle que le mouvement est circulaire uniforme. Quelle relation peut-on alors écrire entre l'accélération a et la vitesse v du centre d'inertie de la Terre autour du Soleil ?
  5. Donner l'expression de la vitesse v du centre d'inertie de la Terre en fonction de la constante de gravitation universelle G, la masse du Soleil Ms et le rayon R de la trajectoire.
  6. Calculer la valeur de cette vitesse.
  7. Donner l'expression de la période de rotation T de la Terre autour du Soleil en fonction de la vitesse v et du rayon R de sa trajectoire.
  8. Montrer alors qu'on peut écrire que T = 2p R3/2/ ( GMs)½, puis calculer sa valeur.
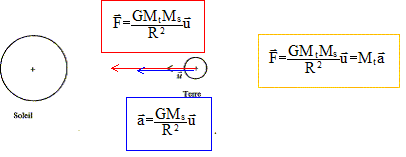
Deuxième loi de Newton :

Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération de son centre d'inertie.

L'accélération est centripète, dirigée vers le centre du soleil, sa valeur est : a = GMs/R2.

Le mouvement est circulaire uniforme.

Relation entre l'accélération a et la vitesse v du centre d'inertie de la Terre autour du Soleil :

a = v2/R.

v : vitesse en m/s et R (m) rayon de l'orbite circulaire.

Valeur de cette vitesse :

a = GMs/R2 = v2/R d'où v2 = GMs/R ; v = [GMs/R]½.

v = [6,67.10-11*1,98.1030 / 1,50 1011]½ =2,97 104 m/s.

Expression de la période de rotation T de la Terre autour du Soleil en fonction de la vitesse v et du rayon R de sa trajectoire :

Durée (s) nécessaire pour décrire une circonférence ( 2pR en mètre) à la vitesse v ( m/s) définie ci-dessus.

2pR = v T ; T= 2pR / v.

 Expression de T en fonction de G, Ms et R :

Elever au carré l'expression de la période : T2 = 4p2 R 2 / v2.

Remplacer v2 par son expression GMs/ R: T2 = 4p2 R 3 / (GMs).

T = 2p[R 3 / (GMs)]½.

Calcul de la période T :

[GMs]½ =[ 6,67.10-11 *1,98.1030]½ =1,1492 1010.

R3/2 =( 1,50 1011)3/2 =5,81 1016.

T = 6,28*5,81 1016/1,1492 1010=3,17 107 s.
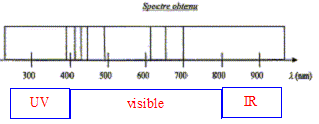
Étude d'une étoile filante :

Il est très rare de pouvoir enregistrer un tel phénomène, celui-ci étant imprévisible. Pourtant, dans la nuit du 12 au 13 mai 2002, alors qu'ils observaient une supernova dans une galaxie éloignée à l'aide du VLT (Very Large Telescope) à l'observatoire de Paranal au Chili, des astronomes ont eu la chance de voir une étoile filante traverser le champ du télescope, et ont pu ainsi enregistrer le spectre de la lumière émise. On donne une partie du spectre obtenu.

  1. Indiquer sur ce spectre les domaines de la lumière visible, des rayonnements infrarouges et ultraviolets.
  2. On donne le diagramme des niveaux d'énergie d'un des éléments mis en évidence par le spectre obtenu. Une transition correspondant à l'une des raies de ce spectre y est représentée par une flèche.

  3. La raie correspondante est-elle une raie d'émission ou d'absorption? Justifier.
  4. Donner l'expression de l'énergie échangée |DE| entre l'atome et le milieu extérieur lors de cette transition. On notera n la fréquence de la radiation lumineuse correspondante.
  5. Donner la relation entre la longueur d'onde l, de cette radiation et sa fréquence n dans le vide.
  6. Déterminer sur le diagramme la valeur de |DE|. Convertir en joule la valeur trouvée.
  7. Calculer alors la valeur de la longueur d'onde l, correspondant à cette transition.
  8. On donne les tableaux de quelques longueurs d'onde de raies de différents éléments. Identifier l'élément mis en évidence par cette raie.

Elément azote : 396; 404 ; 424 ; 445 ; 463 ; 480 ; 505 ; 550 ; 575 ; 595 ; 648 ; 661 nm.

Element oxygène : 391 ; 397 ; 420 ; 442 ; 465 ; 616 ; 700 nm.

Element hydrogène :397 ; 412 ; 436 ; 486 ; 656 nm.

 

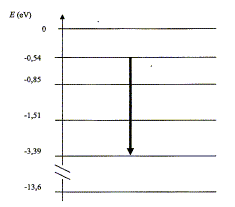
Les domaines de la lumière visible, des rayonnements infrarouges et ultraviolets.

La raie correspondante est une raie d'émission d'un photon : l'atome cède de l'énergie en passant d'un état excité à un état excité de moindre énergie.

Expression de l'énergie échangée |DE| entre l'atome et le milieu extérieur lors de cette transition :

|DE| = h n avec n la fréquence de la radiation lumineuse.

Relation entre la longueur d'onde l, de cette radiation et sa fréquence n :

l = c/n.

|DE| =3,39-0,54 ; |DE| = 2,85 eV. (lecture diagramme ci-dessus)

puis 2,85*1,60 10-19 = 4,56 10-19 J.

Valeur de la longueur d'onde l, correspondant à cette transition :

|DE| = hc/l d'où l = hc/|DE|

l = 6,62.10-34 *3,00.108 /4,56 10-19 =4,36 10-7 m = 436 nm.

Cette raie met en évidence l'élément hydrogène.
 
retour -menu