Aurélie 27/06/07
 

Générateur de rampe, comparateur à un seuil bac sti électronique 2007
. .

Google


Le condensateur étudié précédemment est intégré dans un générateur de rampe. Le comparateur placé à la suite fournit une tension rectangulaire dont la valeur moyenne <u2> est proportionnelle à la capacité C du condensateur.

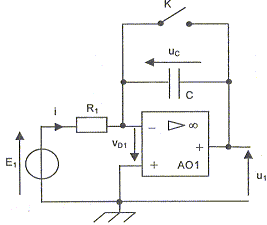
Le générateur de rampe :

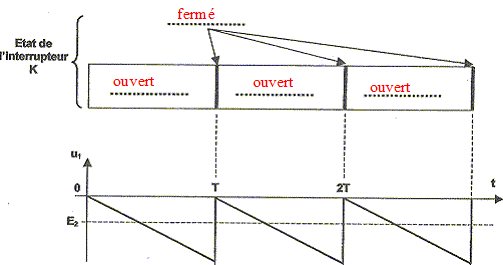
K est un interrupteur parfait commandé périodiquement. E1 est une tension constante.

  1. Quel est le mode de fonctionnement de l'AO1 ? En déduire la valeur de vD1.
  2. Établir une relation entre les tension u1 et uC.
  3. L'interrupteur K est fermé. Que vaut la tension uC ? En déduire la valeur de la tension u1.
  4. À t = 0, K s'ouvre. On considère que u1(0) = 0.
    - Exprimer i en fonction de E1 et R1.
    - Exprimer i en fonction de C et duC/dt (dérivée de uC par rapport au temps).
    - Déduire l'expression de i en fonction de C et du1/dt (dérivée de u1 par rapport au temps).
    - Exprimer du1/dt en fonction de E1, R1 et C.
    -Montrer que la tension u1 évolue selon la relation : u1(t) = E1/(R1C) t.
    - Quelle est l'allure de la tension u1 au cours du temps ?
  5. Les variations de la tension u1 sont représentées ci-dessous. Sur le même document, compléter les pointillés du bandeau "État de l'interrupteur K" par les mentions "Ouvert" ou "Fermé".

mode de fonctionnement de l'AO1 :

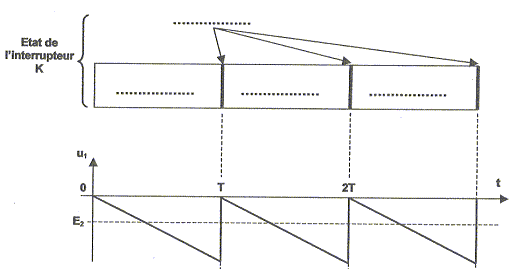
linéaire du fait de la contre réaction entre la sortie et l'entrée inverseuse et de l'absence de liaison entre la sortie et l'entrée non inverseuse

La valeur de vD1 est nulle en mode linèaire.

Relation entre les tension u1 et uC :

L'entrée non inverseue est reliée à la masse et vD1 est nulle : u1 + uC = 0 ; u1 = - uC.

Si l'interrupteur K est fermé la tension uC et en conséquence la tension u1 sont nulles.

À t = 0, K s'ouvre. On considère que u1(0) = 0.
Expression de i en fonction de E1 et R1.

E1=R1 i ; i = E1/R1.
Expression de i en fonction de C et duC/dt :

i = CduC/dt
Expression de i en fonction de C et du1/dt :

u1 = - uC ; du1/dt = - duC/dt ; i = -Cdu1/dt
Expression de du1/dt en fonction de E1, R1 et C.

i = E1/R1 = -Cdu1/dt ; du1/dt = -E1/(R1C)

Par intégration entre les dates t=0 et t :

u1 =-E1/(R1C) t + constante.

Or à t=0 la tension u1 est nulle : la constante d'intégration est donc nulle.

u1(t) = -E1/(R1C) t.
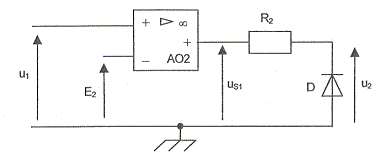
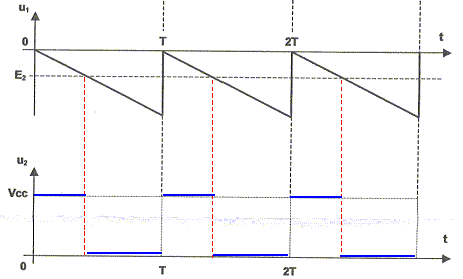
Allure de la tension u1 au cours du temps : droite décroissante passant par l'origine.

 

 
Le comparateur à un seuil :

 

 

  1. Que vaut la tension uS1 si u1 > E2 ? En déduire l'état de la diode D et la valeur de la tension u2.
  2. Que vaut la tension uS1 si u1 < E2 ? En déduire l'état de la diode D et la valeur de la tension u2.
  3. E2 est une tension continue négative. Elle est indiquée en pointillés sur le chronogramme de la tension u1. Représenter l'évolution de la tension u2 sur le document réponse 1 en concordance de temps avec u1.
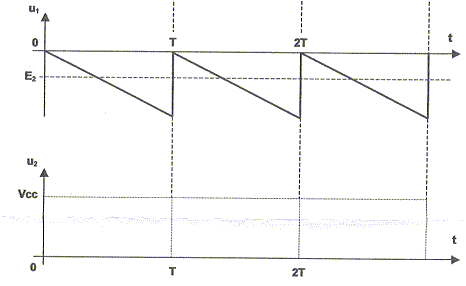
Dans le cas du montage comparateur, la tension de sortie uS1 dépend du signe de de la différence u1-E2.

si u1 > E2 , u1-E2est positive : alors uS1 = + 12 V.

Dans ce cas la diode est non passante ; l'intensité est nulle dans R2 et en conséquence u2 = uS1 = + 12 V.

si u1< E2 , u1-E2est négative : alors uS1 = - 12 V.

Dans ce cas la diode est passante ; la tension à ces bornes est nulle ( diode parfaite) u2 =0 V.

 

 

 

Élaboration de la relation entre <u2> et C

Pour les applications numériques, on prendra les valeurs suivantes :

Générateur de rampe : E1 = 5V ; R1 = 100kW ; T = 240 ms.

Comparateur un seuil : E2 =- 2,5V.

  1. Dans l'intervalle de temps [0,T] (T est la période de la tension u1), on note t1 l'instant pour lequel les tensions u1 et E2 sont égales de sorte que u1(t1) = E2. On rappelle que u1 =-E1/(R1C) t. Exprimer t1 en fonction de E1, R1, C et E2.
  2. Exprimer la valeur moyenne <u2> de la tension u2 en fonction de T, t1 et VCC.
  3. Montrer que <u2> est liée à la capacité C du condensateur par une relation du type : <u2> =k×C.
    - Donner l'expression de k et vérifier que k =2,5 10-3V/pF.
Expression de t1 en fonction de E1, R1, C et E2.

u1 =-E1/(R1C) t1 = E2.

t1 = - E2R1C / E1.

Valeur moyenne <u2> de la tension u2 en fonction de T, t1 et VCC.

Montrons que <u2> est liée à la capacité C du condensateur par une relation du type : <u2> =k×C.

<u2> = VCC( - E2)R1C / (TE1) = VCC( - E2)R1 / (TE1) * C = k C

en posant k = VCC( - E2)R1 / (TE1) .

k= 12*2,5 * 105 / (240 10-6*5 )= 2,5 109 V F-1 = 2,5 10-3 V pF-1.
 
retour -menu