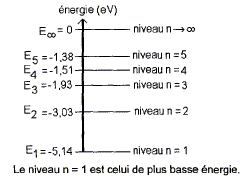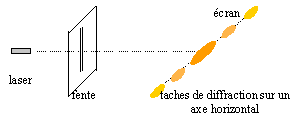|
Lampe à vapeur de sodium, dispersion (prisme), diffraction bac Polynésie 09/07 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts. |
||||||||
|
||||||||
|
Données : masse de l'électron me=9,10 10-31 kg ; masse du proton mp=1,67 10-27 kg ; G= 6,67 10-11 SI ; e = 1,60 10-19 C ; h = 6,63 10-34 J s ; c= 3,00 108 m/s. Etude de l'atome de sodium Donner la composition de l'atome de sodium 2311Na : 11 protons ; 11 électrons ; 23-11 = 12 neutrons. Comment qualifie-t-on l'énergie de l'atome ? Le diagramme énergétique de l'atome de sodium montre que l'énergie ne peut prendre que certaines valeurs. L'énergie de l'atome est quantifiée. La mécanique de Newton permet-elle d'expliquer ces niveaux d'énergie ? La mécanique de Newton permet d'expliquer le monde à l'échelle humaine. Seule
la mécanique
quantique régit
l'infiniment petit de l'atome.
Représenter cette transition par une flèche sur le diagramme énergétique.
Calculer la longueur d'onde l de la radiation émise : D E =hc/ l soit l = hc/ D E. D E =E2-E1 = -3,03 + 5,14 = 2,11 eV 2,11 *1,60 10-19 = 3,376 10-19 J l
= 6,63 10-34 * 3,00
108 /3,376 10-19 =5,89 10-7
m = 589
nm.
l = hc/ D E. La longueur d'onde est d'autant plus petite que la variation d'énergie est plus grande : D E =Eoo-E1 = 0 + 5,14 = 5,14 eV 5,14 *1,60 10-19 = 8,224 10-19 J l = 6,63 10-34 * 3,00 108 /8,224 10-19 =2,42 10-7 m = 242 nm. Préciser, en le justifiant, à quel domaine spectral appartient cette radiation : Cette longueur d'onde étant inférieure à 400 nm ( limite entre le visible et l'UV), elle appartient au domaine ultraviolet.
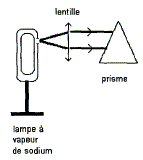
Dispersion de la lumière émise Afin d'étudier la radiation de couleur jaune-orangée, les élèves décident de l'isoler des autres radiations éventuellement émises par la lampe. Pour cela ils réalisent la dispersion de la lumière émise grâce àun prisme de verre. Le verre est un milieu dispersif, expliquer ce terme. Dans un milieu dispersif, la célérité de l'onde dépend de sa fréquence. La fréquence de la radiation jaune-orangée est-elle différente dans le verre et dans l'air ? La fréquence
caractérise une onde : c'est une constante,
indépendante du milieu de propagation.
Définir l'indice de réfraction d'un milieu transparent. L'indice de réfraction, noté n, nombre supérieur à 1, est égal au rapport de la célérité de la lumière dans le vide à la célérité de la lumière dans le milieu considéré. Calculer la longueur d'onde lverre de la radiation jaune-orangée dans le verre. lvide = c/f avec f : fréquence en Hz ; lverre = v/f n = c/v = lvide /lverre ; lverre = lvide / n = 589/1,52 = 387 nm. A la sortie du prisme, on sélectionne la radiation jaune-orangée de longueur d'onde l. Comment qualifie-t-on une telle lumière ? Cette lumière constituée d'une seule radiation est monochromatique.
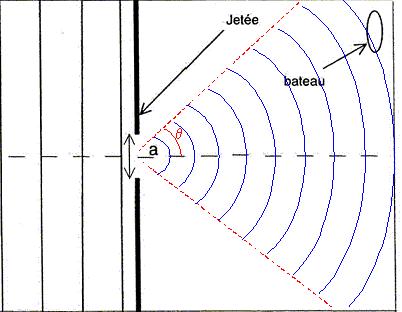
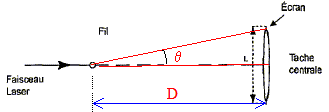
Les élèves décident d'utiliser le phénomène de diffraction pour vérifier la valeur de la longueur d'onde l de la radiation jaune-orangée. Pour cela ils disposent une fente fine verticale sur le trajet de la lumière. Les élèves ont à leur disposition trois fentes de largeur différente. Quel doit être leur choix afin que le phénomène de diffraction soit le plus marqué possible ? La largeur de la fente doit être du même ordre de grandeur que la longueur d'onde de la lumière Le phénomène de diffraction existe-t-il dans d'autres domaines que celui de la lumière ? Si oui donner un exemple avec un schéma explicatif. Le phénomène de diffraction concerne toutes les ondes. Diffraction de la houle ( onde mécanique) par l'ouverture entre les deux jetées.
Derrière la fente, à une distance D= 85 cm, les élèves disposent un écran perpendiculairement à la direction de propagation de la lumière. Dessiner l'allure de ce que l'on observe sur l'écran. Dans la pratique la figure de diffraction est peu lumineuse. La distance L entre deux extinctions, de part et d'autre de la tache centrale, a néanmoins être pu mesurée à l'aide d'une lunette de visée. La valeur L obtenue est L= 2,0 cm. Montrer que la longueur d'onde l peut s'exprimer par l = aL/(2D). tan q = ½L/D voisin de q radian pour les angles petits. largeur angulaire de la tache : 2q = L/D. d'autre part q = l/a. avec : l longueur d'onde (m) et a : largeur de la fente (m) 2l/a=L/D soit l = aL/(2D).
Faire l'application numérique si a = 50 mm. Conclure. l = aL/(2D). a = 50 10-6 m ; L =2,0 10-2 m ; D= 0,85 m. l = 50 10-6 * 2,0 10-2 / 1,7 =5,9 10-7 m. En accord avec la valeur trouvée dans la partie 1 ( 589 nm) |
||||||||
|
|
||||||||
|
|