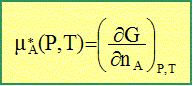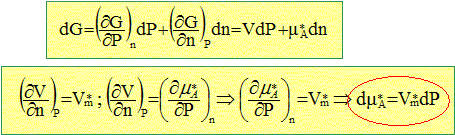Montée de la sève dans les arbres ; pression osmotique concours agrégation 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

On s'intéresse ici à la montée de la sève dans les arbres.

Pression osmotique.

On considère un récipient formé de deux compartiments, gauche et droite, de même volume V et de même température T, séparés par une membrane semi-perméable, c'est à dire perméable au solvant A mais imperméable à un soluté B.

Le compartiment de gauche contient une solution supposée idéale du soluté B dans A, celui de droite le solvant pur sous la pression P.

Rappeler la définition du potentiel chimique m_A*(P,T) du corps pur A à la pression P et à la température T.

On note G(P,T, n_A) la fonction d'état enthalpie libre associée à A, corps pur.

A partir de l'expression de la variation d'enthalpie libre dG, exprimer la variation dm_A* du potentiel chimique du corps pur A en fonction du volume molaire V_m* de A et de la variation de pression dP qui en est la cause à température T fixée.

dG= V dP-SdT+m_A*dn_A

A température constante le terme SdT est nul : dG= V dP+m_A*dn_A. On note n= n_A.

On supposera par la suite que V_m* ne dépend pas de la pression.

Donner l'expression du potentiel chimique du solvant A dans chaque compartiment.

Compartiment de droite : le solvant est pur : m_{A droite} = m _A*(P,T).

Compartiment de gauche : on note x_A la fraction molaire de A et P' la pression dans ce compartiment :

m_{A gauche} = m _A*(P',T) + RT ln x_A.

Le système est à l'équilibre.

 Ecrire la condition d'équilibre que doit vérifier le solvant.

m_{A droite} =m_{A gauche}

m _A*(P,T) = m _A*(P',T) + RT ln x_A.

m _A*(P',T) -m _A*(P,T) = -RT ln x_A.

m _A*(P',T) -m _A*(P,T) = dm _A* = V_m*dP = V_m*(P'-P)

On note p= P'-P

p= -RT / V*_m ln x_A.

Or x_A<1 donc ln x_A<0 et -RT ln x_A>0 donc pest positif.

Il existe une surpression p ( pression osmotique) dans le compartiment de gauche.

La pression osmotique est la pression minimum que l'on doit exercer pour empêcher le passage du solvant d’une solution moins concentrée à une solution plus concentrée, à travers une membrane semiperméable.

On suppose que la solution est peu concentrée et que la membrane est indéformable.

Montrer que la pression osmotique est de la forme p=n_BRT/ V où n_B est la quantité de matière du soluté B.

x_A+ x_B = 1 soit - ln x_A =- ln(1-x_B)

Si x_B <<1 alors - ln(1-x_B) voisin de x_B.

d'où p = RT / V*_mx_B.

x_B = n_B/(n_A+n_B)

En solution diluée ( n_B<<n_A), x_B voisin de n_B/n_A.

d'où p = RT n_B /(n_AV*_m).

En solution diluée n_AV*_m voisin V_droite voisin V_gauche = V.

Par suite : p = RT n_B /V.

A.N : cas de la sève d'érable.

On prendra T= 290 K; masse volumique de la sève : r_sève = 10³ kg m^-3.

La concentration du sucre dans une sève normale , assimilée à une solution aqueuse, est environ C=10 g/L.

Calculer la pression osmotique de la sève par rapport à l'eau du sol autour des racines.

n_B/V =C/M avec M : masse molaire du saccharose C₁₂H₂₂O₁₁.

M = 12*12+22+16*11 = 342 g/mol.

n_B/V = 10/342 = 2,92 10^-2 mol/L = 29,2 mol m^-3.

p = RT n_B /V.

p = 8,32*290* 29,2 = 7,05 10⁴ Pa = 0,70 bar.

p =  r_sève g h.

h = p / ( r_sève g) = 7,05 10⁴ / (10³*9,8) =7,2 m.

La pression osmotique peut-elle expliquer la montée de la sève dans les grands arbres ( hauteur supérieure à 20 m) ?

Non, c'est l'évapotranspiration au niveau des feuilles.

Sous l'action de la chaleur solaire, les feuilles transpirent : l'eau contenue dans les feuilles s'évapore.

Cette évaporation entraîne une dépression dans les canaux qui transportent la sève : il en résulte un effet de succion dans les racines.