Aurélie 21/05/07
 

Diplome d'accès aux études universitaires B Charge et décharge d'un condensateur à travers un résistor. 2005

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

. .
.
.


 

Exercice 1 (7 points)

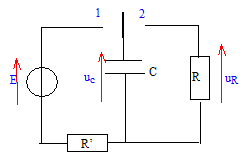
On réalise le circuit électrique suivant :

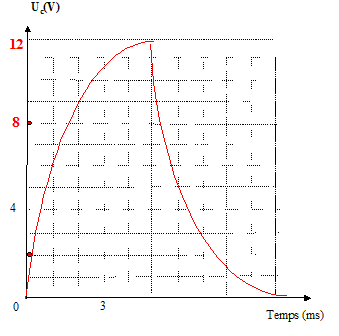
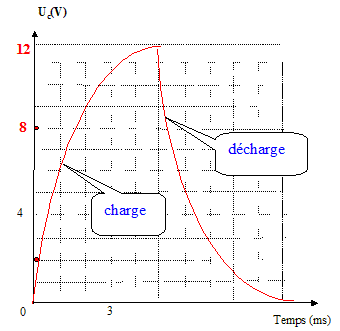
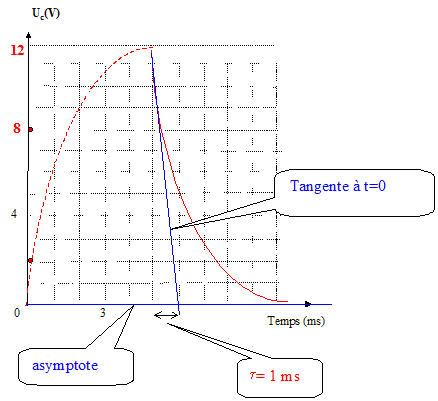
On relève la tension aux bornes du condensateur à l'aide d'un ordinateur avec centrale d'acquisition munie d'un capteur voltmètre. On obtient ainsi les graphes ci-dessous représentant la tension uc(t) aux bornes du condensateur, au cours de sa charge ou de sa décharge.

Lorsque l'interrupteur est en position 1, le condensateur est chargé à travers une résistance R', à l'aide d'un générateur de tension continue de force électromotrice E = 12 V. A l'instant t = 0, alors que le condensateur est complètement chargé, on bascule l'interrupteur en position 2 : le condensateur se décharge dans la résistance R = 500 W.

  1. En appliquant la loi d'additivité des tensions lors de la décharge, établir la relation entre les tensions aux bornes des différents dipôles. Montrer que l'on obtient, pour t > 0 : RC dUc / dt + Uc = 0.
  2. Vérifier que la solution Uc(t) de l'équation différentielle établie peut être exprimée sous la forme : Uc(t) = A exp(-t/(RC)) avec A constante que l'on exprimera à l'aide des conditions initiales.
  3. Attribuer à chaque courbe le phénomène observé : charge ou décharge du condensateur.
  4. Établir l'expression de i(t). Tracer l'allure de la courbe correspondant à i(t) lors de la décharge.
  5. Rappeler l'expression et l'unité de la constante de temps t du dipôle RC. Déterminer sa valeur en utilisant la courbe représentative de la fonction Uc(t). En déduire la valeur de la capacité C du condensateur.


Lorsque l'interrupteur est en position 1, le condensateur est chargé à travers une résistance R', à l'aide d'un générateur de tension continue de force électromotrice E = 12 V. A l'instant t = 0, alors que le condensateur est complètement chargé, on bascule l'interrupteur en position 2 : le condensateur se décharge dans la résistance R = 500 W.

En appliquant la loi d'additivité des tensions lors de la décharge, relation entre les tensions aux bornes des différents dipôles :

tension aux bornes du condensateur Uc ; tension aux bornes du résistor : UR= R i.

Uc =UR= R i.

De plus lors de la décharge i = -dq/dt ( signe moins car la charge dq diminue)

et q= CUc, étant la capacité du condensateur.

d'où i = -CdUc/dt

par suite : RC dUc / dt + Uc = 0. (1)

Vérifioon que la solution Uc(t) de l'équation différentielle établie peut être exprimée sous la forme : Uc(t) = A exp(-t/(RC)) avec A constante :

dériver dUc/dt = A (-1/(RC) exp (-t/(RC)).

repport dans (1) : -A exp (-t/(RC)) + A exp (-t/(RC)) =0

Cette expression est vérifiée quelque soit le temps , donc Uc(t) = A exp(-t/(RC)) est solution de (1).

Expression de A :

A t=0 le condensateur est chargé et Uc= E d'où :

E = A exp(0) = A ; A= E.

Attribuons à chaque courbe le phénomène observé :

Au cours de la charge Uc croït de 0 à E ; au cours de la décharge, Uc décroït de E à 0.

 

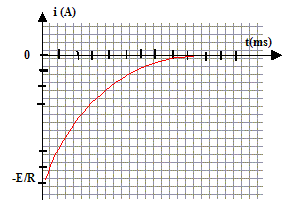
 Expression de i(t) :

i(t) = -CdUc/dt

dUc/dt = -E/(RC) exp (-t/(RC)).

i(t) =-E/Rexp (-t/(RC)).

 

Allure de la courbe correspondant à i(t) lors de la décharge :

La constante de temps t du dipôle RC:

t = RC ; t s'exprime en seconde ou en milliseconde.

Valeur de la capacité C du condensateur.

RC= 10-3 s et R= 500 W

C= 10-3 /500 = 2 10-6 F.


retour -menu