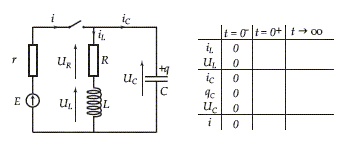concours EPF électricité : dipoles RL, RC. 2006

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

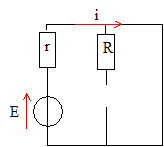
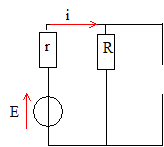
A l’instant de date t = 0, on ferme l’interrupteur. On suppose qu’à t = 0^-, toutes les valeurs du tableau étaient nulles.

- En tenant compte des continuités imposées, d’une part par la bobine, d’autre part par le condensateur et en faisant un

schéma ”équivalent” à t = 0⁺, reproduire le tableau et déterminer toutes valeurs à t = 0⁺.

- En faisant un nouveau schéma ”équivalent” lorsque t--> oo, trouver toutes les valeurs pour t-->oo et compléter votre tableau.

	à t=0+
iL	La bobine retarde l'établissement du courant iL =0
qC	Le condensateur n'a pas eu le temps de se charger : qC =0
UC	qC = CUC ; si qC = 0 alors UC =0. Le condensateur se comporte comme un petit fil de cuivre
i	i= E/r
iC	iC =i= E/r
UL	UL = L [di/dt] t = 0+ = 0

	à t--> oo
iL	Le régime permanent est établit : iL =E/( R+r)
qC	Le condensateur est chargé : qC =UC /C ; qC =E/C
UC	Le condensateur est chargé ; la tension aux bornes du condensateur est égal à E UC =E-ri = E-rE/(R+r) ; UC =E R/(R+r) .
i	i= E/( R+r)
iC	iC =0 ( discontiniuité de l'intensité dans la branche contenant le condensateur )
UL	UL = L [di/dt] t --> oo = 0 ( discontiniuité de la tension aux bornes de la bobine )