concours manipulateur électroradiologie Etude d'une chute libre; analyse dimensionnelle Nantes 2007

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.

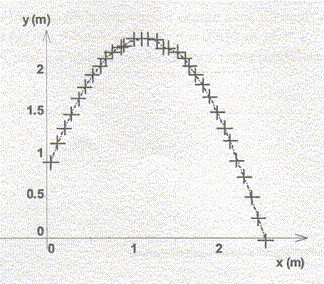
La numérisation de la trajectoire par vidéo montre l'enregistrement suivant :

Les valeurs numériques des positions du centre d'inertie G(x ; y) et les coordonnées du vecteur vitesse ( V_x ; V_y) sont extraites du tableur :

t(s)	x(m)	y(m)	Vx (m/s)	Vy (m/s)
0	0,04347	0,9129	1,96	5,45
0,04	0,1196	1,141	1,999	5,062
0,08	0,2065	1,326	2,038	4,673
0,12	0,2826	1,489	2,038	4,239
0,16	0,3695	1,674	2,038	3,967
0,20	0,4456	1,815	2,092	3,587
.......
1,16	2,391	0,4891	2,092	-6,086
1,2	2,467	0,2391	2,053	-6,63
1,24	2,554	0,000	2,015	-7,173

La boule est soumise à son poids, verticale, vers le bas, valeur P=mg ;

La poussée d'Archimède due à l'air est négligeable devant le poids : la masse volumique de l'air est très inférieure à la masse volumique de la boule.

Les frottements fluides sont négligeables : la vitesse reste faible.

Accélération du centre d'inertie de la boule :

Ecrire la seconde loi de Newton sur un axe vertical ascendant : -mg = ma d'où a = -g.

Un corps est en chute libre lorsqu'il n'est soumis qu'à son poids.

Conditions initiales à t = 0 :
- Les coordonées du centre d'inertie G₀ : x₀ = 0,04347 m ; y₀ = 0,9129 m
- La valeur de la vitesse initiale V₀ :

v_{x 0} = 1,96 m/s ; v_y0 = 5,45 m/s.

v₀ =[ v_{x 0}² + v_{y 0}² ]^½ = [1,96² + 5,45² ]^½ = 5,79 m/s.
- L'angle de lancer a ( en degrés) que fait le vecteur vitesse avec l'horizontale :

tan a = v_{y 0} / v_{x 0} = 5,45 / 1,96 = 2,781 ; a = 70,2 °.

Equations horaires x(t) et y(t).

La vitesse est une primitive de l'accélération : V_x = V_x0 = 1,96 m/s ;

V_y= at+V_y0 =-9,81 t + 5,45.

La position est une primitive de la vitesse :

x = V_x0 t + x₀ ; x = 1,96 t + 0,04347.(1)

y = ½at² + V_yt + y₀ ; y =- -4,905 t² + 5,45 t + 0,9129. (2)

La valeur du vecteur vitesse au sommet S de la trajectoire n'est pas nulle.

Seule la composante verticale de la vitesse est nulle au sommet de la trajectoire ; V_x = 1,96 m/s.

Si la vitesse était nulle au sommet S, la boule marquerait un temps d'arrêt.

Equation de la trajectoire :

(1) donne : t = (x-0,04347) / 1,96

repport dans (2) : y = -4,905 (x-0,04347)² / 1,96² + 5,79 (x-0,04347) / 1,96 +0,9129.

y = -1,28 x² + 2,84 x +0,782.

La modélisation de la trajectoire donne avec un écart expérience-modèle de 1 % :
y(t) = a+bx +c x² où a = 0,812 m ; b= 2,78 ; c = -1,22 m^-1.
Retrouvons la valeur de g :

c = -½g / (v₀cosa)² ; g = -2 c (v₀cosa)² ;

g = -2*(1,22) *(5,79 *cos70,2)² = 9,38 m/s².

L'écart relatif avec la valeur réelle est de 4,4 % : il faudrait tenir compte des frottements afin que le modèle coïncide un peu plus avec la réalité.

Cela est confirmé par le fait que la composante horizontale de la vitesse varie un peu. ( d'après le tableau de valeurs) 

Analyse dimensionnelle : 4 points

Déterminer les dimensions des grandeurs physiques et préciser leur unité.

Célérité des ondes périodiques : longueur / temps ; [v] =L T^-1 (m/s)

Constante radioactive l :

exp(-lt) est sans dimension ; l est l'inverse d'un temps : [l] = T^-1 ( s^-1)

électron-volt ( eV) :

il s'agit d'une énergie donc force * longueur ; or une force est une masse fois une accélération ; une accélération est une longueur divisée par un temps au carré :

[électron-volt] = M L²T^-2 ( 1,6 10^-19 J)

circuit RC: la constante de temps t :

t = RC

R I²t est une énergie ; R : énergie / ( intensité²*temps)

½Q²/C est une énergie ( avec Q = intensité * temps) ; C est : (intensité * temps)²/ énergie.

RC est donc un temps. [t] = T ( s).

circuit RL: la constante de temps t :

t =L/R

R I²t est une énergie ; R : énergie / ( intensité²*temps)

½LI² est une énergie ; L est : énergie / intensité ².

L/R est donc un temps. [t] = T ( s).

circuit RLC: la période T₀ :

T₀ = 2p[LC]^½.

2p : sans dimension

L : énergie / intensité ² ; C : (intensité * temps)²/ énergie.

LC : temps ² ; [LC]^½ est un temps

[T₀]= T (s)