|
Agrégation 2005 : la métallurgie du titane ; diagramme d'Ellingham ; avancement, pression partielle En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptés à vos centres d’intérêts.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
| .
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
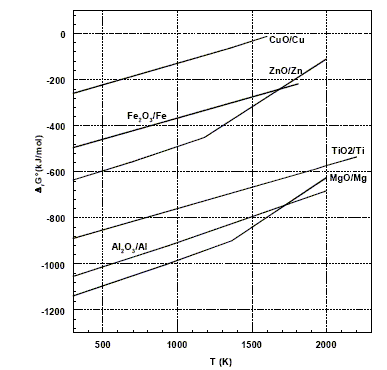
(1) TiO2(s) + 2Cl2(g) + 2C(s) = 2CO(g) + TiCl4(g) à 900°C (2) TiCl4(g) + 2Mg(l) = Ti(s)+ 2MgCl2(l) à 800°C On obtient ainsi le métal titane sous la forme d'éponge qui est ensuite refondue pour obtenir des lingots. La figure ci-dessous donne le diagramme d'Ellingham, rapporté à 1 mol de dioxygène, pour quelques composés.
Principe de construction du diagramme d'Ellingham : On représente l'enthalpie libre DrG°(T) de la réaction suivante en fonction de la température. 2x/y M+ 1 O2 =2/y MxOy. L'entropie DrS° et l'enthalpie DrH° étant supposées indépendantes de la température, les courbes d'équation DrG°(T) = DrH° - T DrS° sont des segments de droites. Les ruptures de pente correspondent à des changements d'états physiques. Prévision du sens d'évolution d'une réaction chimique à l'aide des couples Fe2O3/Fe et Al2O3/Al : 4/3 Al + O2 = 2/3Al2O3 (1) DrG°1. 4/3 Fe + O2 = 2/3Fe2O3 (2) DrG°2. 1, 5 fois (1) - 1,5 fois (2) donne : Fe2O3 + 2Al = 2Fe + Al2O3 DrG° avec DrG° = 1,5 ( DrG°1-DrG°2) Dans le domaine de température proposé, la droite relative à Al2O3/Al est située au dessous de la droite relative à Fe2O3/Fe : en conséquence : DrG°1<DrG°2 et DrG° <0, la réaction évolue dans le sens direct, réduction de Fe2O3. D'après le diagramme ci-dessus, TiO2 ne peut être réduit en métal que par Al et Mg. Ces derniers métaux sont élaborés par électrolyse, processus assez couteux en énergie électrique. La réduction directe de l'oxyde de titane par un métal n'est donc pas utilisée. Beaucoup d'oxydes de métaux peuvent être réduits par le carbone. Dans les conditions opératoires utilisées, c'est le couple CO/C qui est mis en jeu.
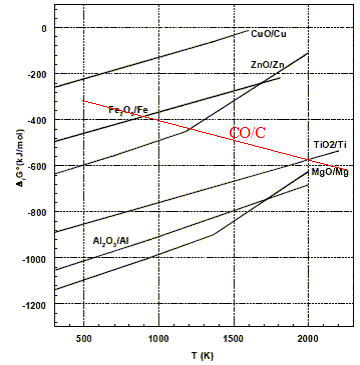
Courbe d'Ellingham pour ce couple dans le domaine de température 500-2000 K ajoutée sur la figure ci-dessus : DrH° = 2DrH°(CO)-DrH°(O2(g))-2DrH°(C graphite ) = -221 kJ/mol DrS° = 2DrS°(CO)-DrS°(O2(g))-2DrS°(C graphite ) = 2*197,6 -2*5,7-205 = 178,8 J mol-1 K-1. DrG °=DrH° -TDrS° = -221 -0,1788 T en kJ/mol. DrG °(500) = -310 kJ/mol ; DrG °(2000) = -579 kJ/mol ;
La réduction de TiO2 par C est possible si la température est supérieure à 2000 K ( température d'inversion de cette réaction). En fait, cette réaction n'est pas utilisée industriellement. On s'intéresse ici à l'équilibre (1) mis en oeuvre dans le procédé Kroll. (1) TiO2(s) + 2Cl2(g) + 2C(s) = 2CO(g) + TiCl4(g) à 900°C En utilisant l'approximation d'Ellingham, montrons que cet équilibre est favorisé dans le sens direct quelque soit la température.
DrH° = -763 -2*110,5 +945 = -39 kJ/mol DrS° = DrS°(TiCl4) +2DrS°(CO)-2DrS°(Cl2(g)-2DrS°(C graphite )- DrS°(TiO2) DrS° = 354,8+2*197,6 -2*223-2*5,7 -50,3= 242 J mol-1 K-1. DrG °=DrH° -TDrS° = -39 -0,242 T en kJ/mol. DrG °<0 quelque soit T : l'équilibre (1) est favorisé dans le sens direct. On une température de 900°C, qui est une température intermédiaire en métallurgie car : - La température est un facteur cinétique favorable. - La réaction étant exothermique, à plus haute température, l'équilibre serait déplacé dans le sens indirect. On peut séparer le chlorure de titane du mélange réactionnel à la suite de cette première étape en abaissant la température à une valeur inférieure à 136 °C, température d'ébullition de TiCl4. Les autres constituants du mélanges étant soit solide, soit gazeux.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(3) TiCl4(g) + O2(g) = TiO2(s) + 2Cl2(g) à 1400°C On étudie cet équilibre à la température de 1400°C à laquelle la constante d'équilibre vaut K' = 230. Le volume total de l'enceinte est de 100 L. On part d'un mélange formé de 2 mol de chacun des réactifs TiCl4 et O2. Quantités de matière
de tous les constituants ainsi que les pressions partielles
des gaz à l'équilibre : xéq
= 1,77 mol 0,23 0,23 1,77 3,54 A l'équilibre : nombre total de mol de gaz N= 4 fractions molaires des gaz : x(TiCl4) = x(O2) =(2-xéq)/N ; x(Cl2) =2xéq /N Les pression partielles sont proportionnelles aux fractions molaires ; P: pression totale. P(TiCl4) =P(O2)= (2-xéq)P/N ; P(Cl2) =2xéq P/N d'où K'= [(2xéq) / (2-xéq)]2 = 230 ; (2xéq) / (2-xéq) = 230½ =15,16 2xéq = 15,16(2-xéq) ; xéq = 1,77 mol. P= NRT/V = 4*8,314*(1400+273) / 0,1 =5,56 105 Pa = 5,56 bars. P(TiCl4) =P(O2)= (2-xéq)P/N = 0,23*5,56/4 = 0,32 bar P(Cl2) =2xéq P/N =2*1,77*5,56/4 =4,91 bars On part de 1 mol de dioxyde de titane et de 20 mol de dichlore. Composition du système lorsqu'il n'évolue plus.
A l'équilibre : nombre total de mol de gaz N= 20 fractions molaires des gaz : x(TiCl4) = x(O2) =xéq/N ; x(Cl2) =(20-2xéq) /N Les pression partielles sont proportionnelles aux fractions molaires ; P: pression totale. P(TiCl4) =P(O2)= xéqP/N ; P(Cl2) =(20-2xéq) P/N d'où K'= [(20-2xéq) / xéq]2 = 230 ; (20-2xéq) / xéq = 230½ =15,16 15,16 xéq = 20-2xéq ; xéq = 1,16 mol. xéq ne peut pas être supérieur à xmax =1 ; il n'y a pas d'équilibre, la réaction est totale. Effet d'une variation de pression totale, à composition constante et température constante, sur l'équilibre (3) : Dans l'expression de K', la pression n'apparaît pas, seul l'avancement y figure : une variation de pression ne modifie pas l'équilibre. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
